I finally got to use the Canon EOS 300D with USM lens. It is brilliant.
Thursday, November 30, 2006
I have arrived in Malaysia in one piece. Updates will be sparse over the next few days.
I finally got to use the Canon EOS 300D with USM lens. It is brilliant.
I finally got to use the Canon EOS 300D with USM lens. It is brilliant.
Tuesday, November 28, 2006
The week in (p)review
Yesterday (Monday), I sold my first ever photographs. In exchange for about 3 hours of services, 150 exposures and 6 frames of 35mm film, I was paid $n, provided with a good lunch (which included 小笼包) and given the opportunity to drive a Mercedes Benz A190.
Here are a few photos of the client from that session.
Here are a few photos of the client from that session.

Click here for large size image

Click here for large size image

Today (Tuesday), I was paid for my second lot of photographs. For photographs of the restaurant’s food which were taken during working hours, I was paid another $n on top of my hourly wages.
A colleague has already expressed interest in getting a group portrait done for his band. He has even gone so far as to ask how much I charge.
Tomorrow (Wednesday) evening, I’ll be heading to Melbourne International Airport.
On Thursday, I’ll be driving myself home from Kuala Lumpur International Airport.
On Friday, it will be the little brother’s birthday party.
On Saturday, it will be 4th Granduncle’s 70th birthday bash.
On Sunday, we will be going to my grandparents place.
Who knows what Monday will bring.
A colleague has already expressed interest in getting a group portrait done for his band. He has even gone so far as to ask how much I charge.
Tomorrow (Wednesday) evening, I’ll be heading to Melbourne International Airport.
On Thursday, I’ll be driving myself home from Kuala Lumpur International Airport.
On Friday, it will be the little brother’s birthday party.
On Saturday, it will be 4th Granduncle’s 70th birthday bash.
On Sunday, we will be going to my grandparents place.
Who knows what Monday will bring.
My bags are still not packed. Shit.
Labels: holidays, personal, photography
Friday, November 24, 2006
The countdown has started
In five days, I will be pushed into a pressurised vessel (in the form of a Boeing 747-400) and flown into Kuala Lumpur with several kilograms of photographic equipment, junk food and clothing.
Application of full throttle on the 747’s four turbofan engines would be a notable event marking the end of a significant phase of my life.
The past 6 months had been amazing. I learned to be financially self sufficient (taking money from my parents after becoming eligible for professional employment would be extremely unethical). Waiting tables improved my self-confidence. My Chinese improved a fair bit. I took a lot of photographs. I looked for and found a professional job. I met a remarkable person. I no longer find gays scary (except for the weirdest ones).
The lifestyle was wonderful. Averaging at about 16 hours of work weekly and not having any lectures to worry about, I had lots of time. I could drift out for a coffee or breakfast together with office workers having their lunches. Or I could freeload on magazines at the bookshop while everyone else was busy working or studying, then flit off to dinner.
My graduation last year was for my parents- they had successfully raised a son to the level of Bachelor of Engineering (Mechanical). For me, there was no sense of achievement. All tuition fees and expenses were paid by my parents. Due to luck, the final project was remarkably stress-free. The ceremony felt hollow, tedious even. But don't get me wrong, I am grateful.
This six months, however, are almost entirely mine. Almost, because significant credit must be still given to my parents, Tracey, May and David.
At the end of my undergraduate degree, I was fretting about having to stop bumming, start working and be responsible. Now that I am a bit tired of waiting tables (after having figured out how to coax the coffee machine to help me pour latte-art), professional work and the associated money is starting to look attractive.
In five day’s time, I will be flying home for a holiday, then to Beijing on the 24th. I’ll start work several days after I get back to Melbourne. Then, a new phase would start.
But first, I’m off to think about packing.
***
This afternoon brought with good weather and bad developments. Sigh. :(
PS: I just realised that I wrote "I met a remarkable person. I no longer find gays scary." They are in no way connected.
Application of full throttle on the 747’s four turbofan engines would be a notable event marking the end of a significant phase of my life.
The past 6 months had been amazing. I learned to be financially self sufficient (taking money from my parents after becoming eligible for professional employment would be extremely unethical). Waiting tables improved my self-confidence. My Chinese improved a fair bit. I took a lot of photographs. I looked for and found a professional job. I met a remarkable person. I no longer find gays scary (except for the weirdest ones).
The lifestyle was wonderful. Averaging at about 16 hours of work weekly and not having any lectures to worry about, I had lots of time. I could drift out for a coffee or breakfast together with office workers having their lunches. Or I could freeload on magazines at the bookshop while everyone else was busy working or studying, then flit off to dinner.
My graduation last year was for my parents- they had successfully raised a son to the level of Bachelor of Engineering (Mechanical). For me, there was no sense of achievement. All tuition fees and expenses were paid by my parents. Due to luck, the final project was remarkably stress-free. The ceremony felt hollow, tedious even. But don't get me wrong, I am grateful.
This six months, however, are almost entirely mine. Almost, because significant credit must be still given to my parents, Tracey, May and David.
At the end of my undergraduate degree, I was fretting about having to stop bumming, start working and be responsible. Now that I am a bit tired of waiting tables (after having figured out how to coax the coffee machine to help me pour latte-art), professional work and the associated money is starting to look attractive.
In five day’s time, I will be flying home for a holiday, then to Beijing on the 24th. I’ll start work several days after I get back to Melbourne. Then, a new phase would start.
But first, I’m off to think about packing.
This afternoon brought with good weather and bad developments. Sigh. :(
PS: I just realised that I wrote "I met a remarkable person. I no longer find gays scary." They are in no way connected.
Labels: personal
7 Apples
One of the advantages of working in St Kilda (Melbourne) is the proximity to 7 Apples, a gelateria.
It is so good that I end up getting a cone every 2 working days or so (which is equivalent to 3 or 4 times every fortnight). This habit might not be very good on the calorific front, but Iam not can't be bothered counting. It is not cheap too ($3.90), but the tips from each shift are usually more than enough to pay for my ice cream hits.

Click here for large size image
Click here for Deviant Art entry

Click here for large size image
Notice I only started taking photos after the gelato was gone.
7 Apples is located 75, Ackland Street. Take the 96 tram towards St Kilda Beach and get off one stop after Luna Park. The green coloured shop is located on the right just before the tram stops. Beware of the queue on hot weekends.
***
On a completely different note, here is a sky shot. A 24mm lens would be nice.

It is so good that I end up getting a cone every 2 working days or so (which is equivalent to 3 or 4 times every fortnight). This habit might not be very good on the calorific front, but I

Click here for large size image
Click here for Deviant Art entry

Click here for large size image
Notice I only started taking photos after the gelato was gone.
7 Apples is located 75, Ackland Street. Take the 96 tram towards St Kilda Beach and get off one stop after Luna Park. The green coloured shop is located on the right just before the tram stops. Beware of the queue on hot weekends.
On a completely different note, here is a sky shot. A 24mm lens would be nice.

Labels: food, Melbourne, photography
Wednesday, November 22, 2006
Photoelasticity: photographic representation of residual stresses
Note: No image enhancements performed on the following photograhs.
Click here for large size image

Click here for large size image

Click here for large size image

Click here for large size image

Click here for large size image

Click here for large size image

This is cropped from the previous image. The image spans 2mm.

Click here for large size image

Click here for large size image
Certain transparent materials’ optical properties change when stressed. This property can be used to study stress distributions in complicated objects.
One particular application of such a stress-dependent optical property is photoelasticity. The process is described in an extremely brief and (probably) inaccurate manner below:
For the real science behind photoelasticity, this is a good place to start looking.
One particular application of such a stress-dependent optical property is photoelasticity. The process is described in an extremely brief and (probably) inaccurate manner below:
Two polarizers are alighed so that their directions of polarisation are perpendicular. No light can pass through this set up.
A transparent plastic model is placed between these polarizers.
The plastic changes the polarisation of light passing through, such that light that passes through the model can then pass through the second polarizer.
Regions with different stresses change the optical properties in varying manners, and the stress distribution in the model can be observed visually
I would conjecture that the stress is proportional to the density of fringes, and in directions perpendicular to the fringes.
For the real science behind photoelasticity, this is a good place to start looking.

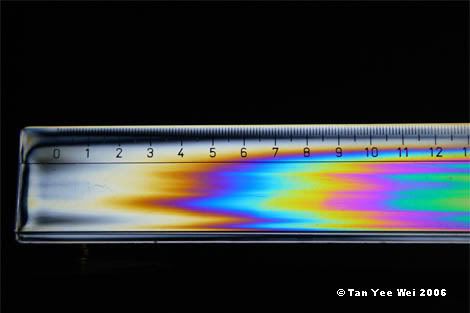
Click here for large size image
The stretched patterns along the ruler suggest that the manufacture of this item involved extrusion or rolling. The hole was then punched, resulting in residual stresses visible around it. There is a discontinuity between the 23rd and 24th cm marks, suggesting some sort of defect, probably a (shallow) surface crack. Stresses do not spread across the gap, resulting in different stress distributions across the crack.

Click here for large size image
It is possible that this set-square was injection moulded. Molten plastic was forced at high pressure into the mould from three nozzles located at the corners of the set-square. The material then flowed outward, filling up the straight edges. Material from 2 different injection ports would meet partway along the straight edges.

Click here for large size image

Click here for large size image
And of course, every geeky photoshoot must be accompanied with some sort of microscopy. Here, the image spans a length of approximately 8mm.

This is cropped from the previous image. The image spans 2mm.
The density of fringes on this stump shows that very large residual stresses are present in this part.
Labels: applied science, microscopy, photography
Sunday, November 19, 2006
Fun with a flashgun, part 2.
Continued from Part 1.
The upper level of the restaurant is wonderful for flash photography: it has a moderately low ceiling of white plaster. Point the flash upwards and extend it's coverage to 24mm. The diffused light from the ceiling gives very gentle shadows and no harsh reflections.


Click here for large size image
I can pour latte-art too!

G
Click here for large size image

V
Click here for large size image

S
Click here for large size image
The upper level of the restaurant is wonderful for flash photography: it has a moderately low ceiling of white plaster. Point the flash upwards and extend it's coverage to 24mm. The diffused light from the ceiling gives very gentle shadows and no harsh reflections.


Click here for large size image
I can pour latte-art too!

G
Click here for large size image

V
Click here for large size image

S
Click here for large size image
Labels: photography
Saturday, November 18, 2006
Fun with a flashgun- Nikon SB-26

Squares
Click here for large size image
I borrowed a flashgun from Lee CF today. It is a wicked Nikon SB-26, with a hot shoe connection, PC-synch terminals (male and female), swivelling and tilting zoom head (20-85mm) and a guide number of 35 m.
Shooting modes include automatic, manual, TTL and strobe. Automatic mode uses an on-board sensor to detect the flash strength required for proper exposure (after feeding in the correct camera parameters into the flash unit). Manual is precisely that, manual. The only variable is the power output, which can be reduced as powers of 2. Full power, 1/2, 1/4, 1/8, 1/16, 1/32 and 1/64. TTL mode is only available to Nikon cameras that can communicate with the flash unit via additional contacts.
Shooting modes include automatic, manual, TTL and strobe. Automatic mode uses an on-board sensor to detect the flash strength required for proper exposure (after feeding in the correct camera parameters into the flash unit). Manual is precisely that, manual. The only variable is the power output, which can be reduced as powers of 2. Full power, 1/2, 1/4, 1/8, 1/16, 1/32 and 1/64. TTL mode is only available to Nikon cameras that can communicate with the flash unit via additional contacts.

Not an Advertisement
Click here for large size image
Strobe mode makes the unit behave like a stroboscope. The parameters that can be adjusted in this mode are: flash intensity, number of flashes, and flash frequency. The frequency can be adjusted from 1 to 50 Hz. Of course, the number of flashes depends on the frequency and intensity of each flash.
I did some flash tests. A powerful and directional flash head does wonders to the lighting. Directing the light at the ceiling results in very even lighting that does not make the pimples shine nor does it cast sharp shadows.
I did some flash tests. A powerful and directional flash head does wonders to the lighting. Directing the light at the ceiling results in very even lighting that does not make the pimples shine nor does it cast sharp shadows.

Click here for large size image

Click here for large size image
Ok, I look freaky here. I was staring at the countdown light on the camera, hence the evil eye.
Please stop judging my eye. It is a good eye. Wankers.
The preceding shots were done using two cameras. The digital camera was used to capture the scene while the film SLR was used to trigger the flash. The flash was pointed forward and upwards to light the wall and ceiling. The digital camera was pre-focused, exposure set to 2s, and the self timer set to 10s. Windows blinds were drawn and the lights were extinguished. The timer was tripped and the subject positioned in place. When the shutter opened, the subject triggered his camera to produce the illumination. The SLR camera’s shutter was then recocked without advancing the film as to avoid (further) wasting film.
I suddenly have this want for a large flashgun. Something powerful with variable power output and a directional head.
I suddenly have this want for a large flashgun. Something powerful with variable power output and a directional head.
Labels: photographic equipment, photography, reviews
Thursday, November 16, 2006
e - unifying two common definitions of e
Note: The concept of infinity would be used liberally here. For a brief introduction to the origins of the infinities found in today's context, read this post.
Perhaps the most common expression that gives the value of e would be the sum of the reciprocal of factorials, from zero to infinity.

Equation (1)
Another well known expression is:
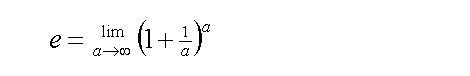
Equation (2)
I will attempt to show that these two expressions are identical. Firstly, I will let a be a finite number before pushing it towards the great infinity.
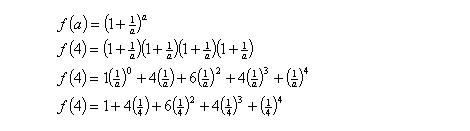
Equations (3)
Here, a takes the value of 4. Expanding the brackets, we see that the terms are results of multiplication between 1 and ¼. In the last line above, the coefficients 1, 4, 6, 4, 1 are actually binomial coefficients resulting from 4C0, 4C1, 4C2… 4C4.
For example, 4C2=6 arises because (¼)^2 appears 6 times as a result of the 6 different ways the terms can combine to give (¼)^2. The combinations are:
If you have no idea what I am talking about, try expanding f(6) into individual terms. It should become clear after that.
f(a) can then be rewritten as
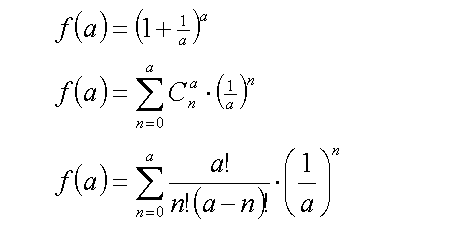
Equations (4)
Expressing the binomial number as a ratio of factorials gives the final line in Equations (4).
Substituting f(a) into the definition of e (equation 2):
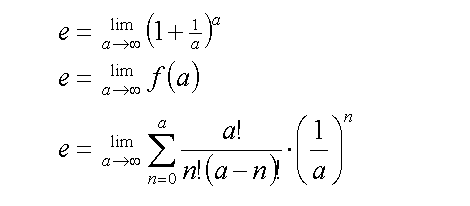
Equations (5)
The equation is beginning to resemble the infinite sum of inverse factorials:
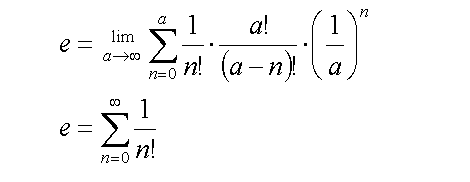
Equations (6)
To show that these equations are equivalent, the following expression needs to be true:
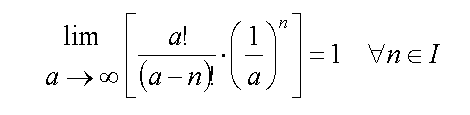
Equations (7)
When a approaches infinity, the terms in the brackets should converge to unity, and the expressions in equations (6) would be identical.
Expanding the terms in the bracket:
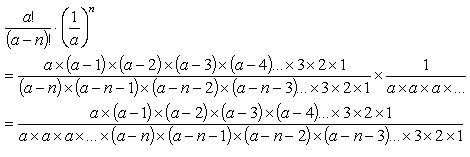
Equations (8)
Cancelling terms that appear in the numerator and denominator:
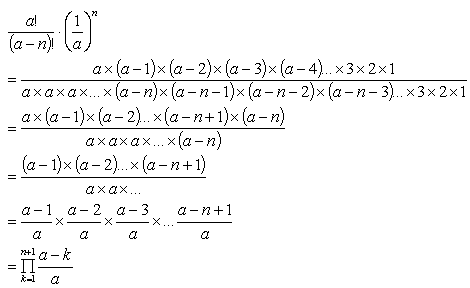
Equations (9)
Note that there are an equal number of terms in the numerator and denominator. For (a-n)!, the missing terms are replaced with the a^n.
Replacing this result into the previous expression:
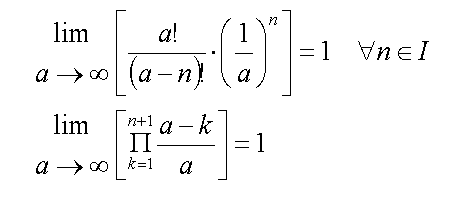
Equations (10)
When taking the limit of a approaching infinity, (a-k)/a is unity regardless of the value of k. After all, infinity minus 5 is still infinity.
Thus, it summary
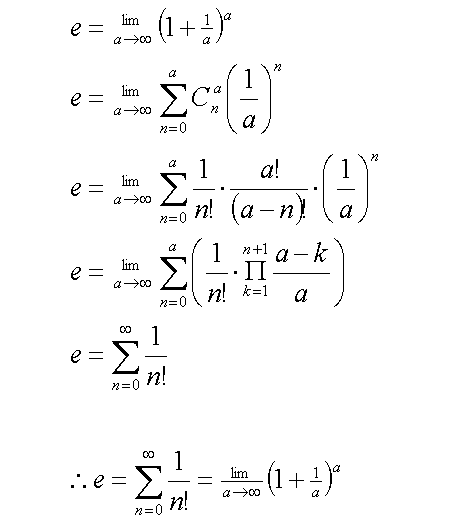
Equations (11)
One very valid concern is, “what happens when k ≈ a? When k ≈ a, (a-k)/a is no longer unity and equation (6) might not match term-for-term.”
Fortunately, this never happens. Observe how the equation is structured: first, let a approach infinity. Then, incrementally increase n and k.
n and k can be as humongous as one wishes to make it, but they would always be dominated by a. You can even make n and k as large as the second Skewe’s number, and they would still not make a dent in a. The second Skewe’s number is finite; a is not.
Perhaps the most common expression that gives the value of e would be the sum of the reciprocal of factorials, from zero to infinity.

Equation (1)
Another well known expression is:
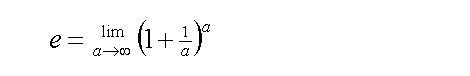
Equation (2)
I will attempt to show that these two expressions are identical. Firstly, I will let a be a finite number before pushing it towards the great infinity.
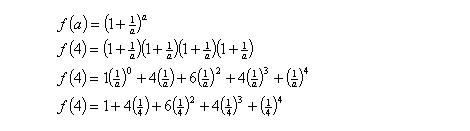
Equations (3)
Here, a takes the value of 4. Expanding the brackets, we see that the terms are results of multiplication between 1 and ¼. In the last line above, the coefficients 1, 4, 6, 4, 1 are actually binomial coefficients resulting from 4C0, 4C1, 4C2… 4C4.
For example, 4C2=6 arises because (¼)^2 appears 6 times as a result of the 6 different ways the terms can combine to give (¼)^2. The combinations are:
Multiply ¼ from the 1st and 2nd brackets, and multiply with 1 from the 3rd and 4th brackets.
Multiply ¼ from the 1st and 3rd brackets, and multiply with 1 from the 2nd and 4th brackets.
Multiply ¼ from the 1st and 4th brackets, and multiply with 1 from the 2nd and 3rd brackets.
Multiply ¼ from the 2nd and 3rd brackets, and multiply with 1 from the 1st and 4th brackets.
Multiply ¼ from the 2nd and 4th brackets, and multiply with 1 from the 1st and 3rd brackets.
Multiply ¼ from the 3rd and 4th brackets, and multiply with 1 from the 1st and 2nd brackets.
If you have no idea what I am talking about, try expanding f(6) into individual terms. It should become clear after that.
f(a) can then be rewritten as
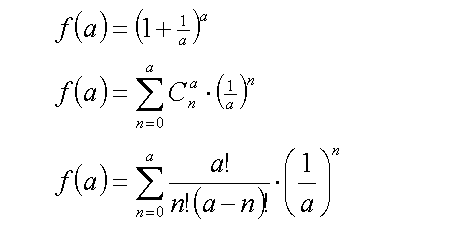
Equations (4)
Expressing the binomial number as a ratio of factorials gives the final line in Equations (4).
Substituting f(a) into the definition of e (equation 2):
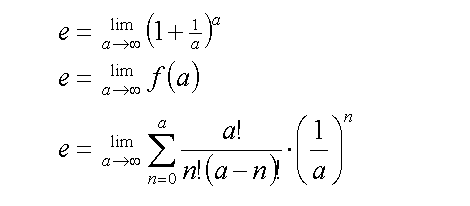
Equations (5)
The equation is beginning to resemble the infinite sum of inverse factorials:
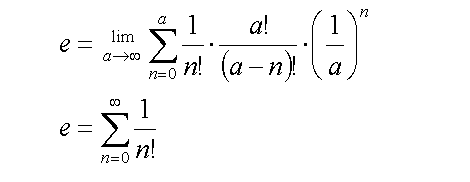
Equations (6)
To show that these equations are equivalent, the following expression needs to be true:
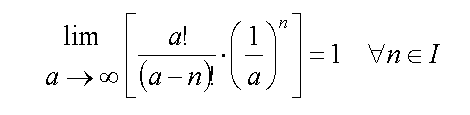
Equations (7)
When a approaches infinity, the terms in the brackets should converge to unity, and the expressions in equations (6) would be identical.
Expanding the terms in the bracket:
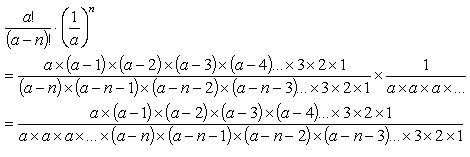
Equations (8)
Cancelling terms that appear in the numerator and denominator:
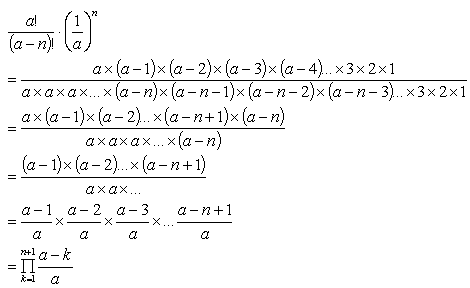
Equations (9)
Note that there are an equal number of terms in the numerator and denominator. For (a-n)!, the missing terms are replaced with the a^n.
Replacing this result into the previous expression:
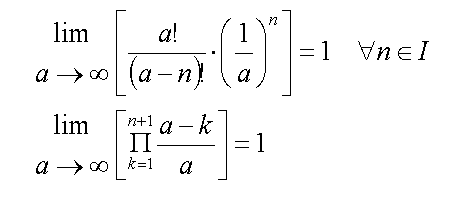
Equations (10)
When taking the limit of a approaching infinity, (a-k)/a is unity regardless of the value of k. After all, infinity minus 5 is still infinity.
Thus, it summary
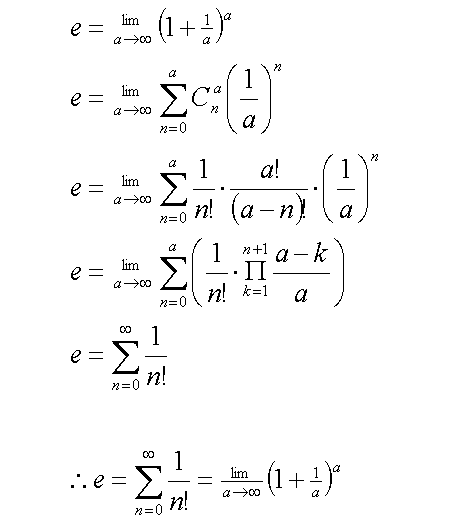
Equations (11)
One very valid concern is, “what happens when k ≈ a? When k ≈ a, (a-k)/a is no longer unity and equation (6) might not match term-for-term.”
Fortunately, this never happens. Observe how the equation is structured: first, let a approach infinity. Then, incrementally increase n and k.
n and k can be as humongous as one wishes to make it, but they would always be dominated by a. You can even make n and k as large as the second Skewe’s number, and they would still not make a dent in a. The second Skewe’s number is finite; a is not.
Labels: mathematics, real numbers
Wednesday, November 15, 2006
Burnt dwelling- photographs

Charred Rafters
Click here for large size image
Click here for Deviant Art entry

Neglected Valve
Click here for large size image

Charcoal
Click here for large size image
Labels: photography
Real numbers – the slippery slope to insanity
Let’s build real numbers from scratch using the Dedekind cut. Use the square root of 2 as an example. Does √2 exist? Specifically, is there an x that can satisfy the equation x^2 = 2 (x squared = 2)?
As the Ancient Greeks already knew, x is definitely not a rational number (fractions and whole numbers). With an understanding that extends only to the rational numbers, how can x be created using and building from existing knowledge?
To perform the Dedekind cut, group all the rational numbers into two sets a and b as follows:
a = {x : x^2}
b = {x : x^2 > 2}
The set a contains all the rational numbers that are less than two when squared; b is the opposite. A few of the elements in a and b are:
a = {1.03, 0.2432, -1.2, …}
b = {3.5, 2.72, -342.22, …}
I must stress this again: all elements in a and b are rational numbers. We currently trying to construct the concept of real numbers from rational numbers.
Interestingly, there is no largest element in a. Give my any element in a and I can find you another element (still in a) that is larger than yours, despite the constraint imposed upon by the rule that all elements in a must obey x^2 a is constructed (it only has elements that squares to less than two), all elements in a will never exceed a certain value. For example, the elements in a will definitely not exceed 19, because 19 squared is 361, definitely greater than 2. We say that 19 is an upper bound of a. No element in a exceeds 19.
But 19 is a very boring upper bound for a. It is like saying "the population of China is definitely less than 27 trillion." Duh.
We can use a smaller value for the upper bound of a, maybe 12. 12 squared is 144, which is greater than 2. For sure, no element in a will be greater than 12.
The upper bound of a can be made smaller and smaller, using 10, 7.4, 5.4, 3.5, 1.5…
And here comes the crucial step: the least upper bound of a is the square root of 2. From two groups of rational numbers, we have conjured a real number.
Recall that there is no largest element of a. Similarly, there is no smallest element of b (ignoring the signs). Like in the previous illustration, we can write a list of elements of b, all of them decreasing and there would never be a smallest element.
5.4
2.54
2.1
1.5
1.46
1.4149
1.4142135626
Interestingly, the least upper bound of a does not lie in a and does not lie in b (after all, a and b can only contain rational numbers). The definitions of sets a and b leave an infinitesimally small gap between them, a gap that can only fit one (real) number- √2.
And that’s all there is to creating real numbers from rationals. It probably feels a little inadequate, a little unsatisfying- as if the real number was not properly created. But bear in mind that the Dedekind cut is merely creating the concept of real numbers. It tells us that the square root of two is not some dodgy product of black magic, but is in fact a very real number.
What the Dedekind cut does not do is tell us the value of √2. It cannot do that. Nothing can- our only understanding of √2 is that it satisfies the equation x^2=2.
We can make approximations (x ≈ 1.4142135624 ), we can generate algorithms to tell us the 96 millionth digit in √2, but we can never know the exact value of √2- it has infinitely many digits.
Mathematics & Applied Sciences
As the Ancient Greeks already knew, x is definitely not a rational number (fractions and whole numbers). With an understanding that extends only to the rational numbers, how can x be created using and building from existing knowledge?
To perform the Dedekind cut, group all the rational numbers into two sets a and b as follows:
a = {x : x^2}
b = {x : x^2 > 2}
The set a contains all the rational numbers that are less than two when squared; b is the opposite. A few of the elements in a and b are:
a = {1.03, 0.2432, -1.2, …}
b = {3.5, 2.72, -342.22, …}
I must stress this again: all elements in a and b are rational numbers. We currently trying to construct the concept of real numbers from rational numbers.
Interestingly, there is no largest element in a. Give my any element in a and I can find you another element (still in a) that is larger than yours, despite the constraint imposed upon by the rule that all elements in a must obey x^2 a is constructed (it only has elements that squares to less than two), all elements in a will never exceed a certain value. For example, the elements in a will definitely not exceed 19, because 19 squared is 361, definitely greater than 2. We say that 19 is an upper bound of a. No element in a exceeds 19.
But 19 is a very boring upper bound for a. It is like saying "the population of China is definitely less than 27 trillion." Duh.
We can use a smaller value for the upper bound of a, maybe 12. 12 squared is 144, which is greater than 2. For sure, no element in a will be greater than 12.
The upper bound of a can be made smaller and smaller, using 10, 7.4, 5.4, 3.5, 1.5…
And here comes the crucial step: the least upper bound of a is the square root of 2. From two groups of rational numbers, we have conjured a real number.
Recall that there is no largest element of a. Similarly, there is no smallest element of b (ignoring the signs). Like in the previous illustration, we can write a list of elements of b, all of them decreasing and there would never be a smallest element.
5.4
2.54
2.1
1.5
1.46
1.4149
1.4142135626
Interestingly, the least upper bound of a does not lie in a and does not lie in b (after all, a and b can only contain rational numbers). The definitions of sets a and b leave an infinitesimally small gap between them, a gap that can only fit one (real) number- √2.
And that’s all there is to creating real numbers from rationals. It probably feels a little inadequate, a little unsatisfying- as if the real number was not properly created. But bear in mind that the Dedekind cut is merely creating the concept of real numbers. It tells us that the square root of two is not some dodgy product of black magic, but is in fact a very real number.
What the Dedekind cut does not do is tell us the value of √2. It cannot do that. Nothing can- our only understanding of √2 is that it satisfies the equation x^2=2.
We can make approximations (x ≈ 1.4142135624 ), we can generate algorithms to tell us the 96 millionth digit in √2, but we can never know the exact value of √2- it has infinitely many digits.
Mathematics & Applied Sciences
Labels: mathematics, real numbers
Sunday, November 12, 2006
Sofitel Melbourne- possibly Melbourne's public toilet with the best view

Sofitel's Loo
Click here for large size image (206 kb and about 3 screens wide)
Click here for Deviant Art entry
Horizontal angle of view: ~140°

Sofitel Melbourne is located at 25 Collins Street, near the intersection of Exhibition and Collins Streets.
To access this washroom, take the lifts at Sofitel's lobby up to the 35th floor and turn left upon exiting the lifts. The toilets are a short walk away on the right side.
The window faces approximately 15° south of East. The angle of view is a little less than 180°.
Visit this for sun and moon rise times and azimuth angles in Melbourne, published times not adjusted for summer daylight saving.
To access this washroom, take the lifts at Sofitel's lobby up to the 35th floor and turn left upon exiting the lifts. The toilets are a short walk away on the right side.
The window faces approximately 15° south of East. The angle of view is a little less than 180°.
Visit this for sun and moon rise times and azimuth angles in Melbourne, published times not adjusted for summer daylight saving.
Photographs
Labels: Melbourne, panoramic, photography
Saturday, November 11, 2006
Justifying this page’s existence
Every now and then, the topic of the aims of blogging crops up. I might as well do mine now.
Why I do it:
To show off that I can take photographs, that I know my mathematics, that I can handle non-classical physics, that I can write rubbish. In other words, attention whoring.
To keep my idea organisation and presentation skills sharp
To practice my Chinese
As a dump for the dirty thoughts that would otherwise clog up my cranium
To let friends and family (those that read anyway) know I am still alive and doing things
What I have gained from this little game:
Met a few more people: Diana, Jean, Pamela, Wuching, Yvy
Got myself a job
Reading those interesting people on the right
A bit more about the job hunt adventure:
The advertisement said they were looking for someone with "technical and presentation skills". For the interview, I printed the following articles as my portfolio:
A general handwaving guide to digital photography
The JFE 8555 problem revisited- digital roots
Experimental results on the Panasonic DMC-FZ30’s macro focal distance and magnification factor throughout its zoom range
Floor cleaning algorithms
Intake Horns- an excerpt from the draft of 'Automotive Engines'
“This paper is on pure mathematics, number theory. It proves that digital roots can be obtained by summing digits in any order. And this is one on automotive engineering. It is presented at a level suitable for an interested non-engineer. It also shows my idea presentation skills, where the concepts are incrementally changed to transform intake manifolds into induction horns. And this is a guide to photography written with minimum technicalities [blablabla…]”
I got the job.
(this section is a good example of ‘showing off’)
Interesting reads
Why I do it:
To show off that I can take photographs, that I know my mathematics, that I can handle non-classical physics, that I can write rubbish. In other words, attention whoring.
To keep my idea organisation and presentation skills sharp
To practice my Chinese
As a dump for the dirty thoughts that would otherwise clog up my cranium
To let friends and family (those that read anyway) know I am still alive and doing things
What I have gained from this little game:
Met a few more people: Diana, Jean, Pamela, Wuching, Yvy
Got myself a job
Reading those interesting people on the right
A bit more about the job hunt adventure:
The advertisement said they were looking for someone with "technical and presentation skills". For the interview, I printed the following articles as my portfolio:
A general handwaving guide to digital photography
The JFE 8555 problem revisited- digital roots
Experimental results on the Panasonic DMC-FZ30’s macro focal distance and magnification factor throughout its zoom range
Floor cleaning algorithms
Intake Horns- an excerpt from the draft of 'Automotive Engines'
“This paper is on pure mathematics, number theory. It proves that digital roots can be obtained by summing digits in any order. And this is one on automotive engineering. It is presented at a level suitable for an interested non-engineer. It also shows my idea presentation skills, where the concepts are incrementally changed to transform intake manifolds into induction horns. And this is a guide to photography written with minimum technicalities [blablabla…]”
I got the job.
(this section is a good example of ‘showing off’)
Interesting reads
Wednesday, November 08, 2006
An SLR of my own
After getting a shock when I went to a used photographic equipment shop, I went onto ebay in seach of better deals.
I got a 1982 Ricoh KR-10 Super for $22, much cheaper than the 1984 Pentax Program-A that was selling for a blood-sucking $225 at the shop.
It came in the mail yesterday afternoon.

Click here for large size image
The 50mm f/2.0 lens that came along with it is a dodgy specimen. I intend to hunt for a better one, something fast, hopefully to the tune of f/1.4 and $70.
Meanwhile, my 28-105mm zoom lens has a mount to call its home.

Click here for large size image

Click here for large size image
This camera will be going to Beijing.
Photographs
I got a 1982 Ricoh KR-10 Super for $22, much cheaper than the 1984 Pentax Program-A that was selling for a blood-sucking $225 at the shop.
It came in the mail yesterday afternoon.

Click here for large size image
The 50mm f/2.0 lens that came along with it is a dodgy specimen. I intend to hunt for a better one, something fast, hopefully to the tune of f/1.4 and $70.
Meanwhile, my 28-105mm zoom lens has a mount to call its home.

Click here for large size image

Click here for large size image
This camera will be going to Beijing.
Photographs
Labels: photographic equipment, photography
Sunday, November 05, 2006
Three Colours, Two Photographs and One new driver on the way

Yellow, Green and Blue
Click here for large size image
Click here for Deviant Art entry

Gold, Barred
Today, a certain learner driver drove without her 'L' plates for more than 100 km. There were winding C-roads, sensuously curvy B-roads, fast A-roads, the dual-carraigeway M79, the traffic-lights speckled city grid and the characterless suburban sprawl.
She even eases off the brake pedal at the last moment. And prefers the handling of the Toyota Corolla to the Holden Viva.
Photographs
Labels: holidays, personal, photography
Friday, November 03, 2006
Wednesday, November 01, 2006
A few days ago, I somehow mentioned to my housemate that Malaysia has a significant minority of Indians. He was surprised, and was curious if they brought their own culture (from India) or assimilated into the existing culture.
He said he was interested because Australia is seeing a lot of Indian immigrants recently, and he is not keen on Melbourne turning into “Little India”.
This coming from a white Australian’s mouth is extremely ironic, because Australia is Little Britannia.
He said he was interested because Australia is seeing a lot of Indian immigrants recently, and he is not keen on Melbourne turning into “Little India”.
This coming from a white Australian’s mouth is extremely ironic, because Australia is Little Britannia.
On another note, I have confirmed and paid for my air ticket back home. I’ll be arriving on the 30th of November and departing on the 3rd of January. This is probably a good time to start collecting reading material for the flight. Wuxia novels sound like a good option- the plots are sufficiently engaging and I read pathetically slowly. Also, downloaded and printed sheets do not take up much space.
The restaurant I work at might be redoing the menus to incorporate photographs of the dishes. And I’ll be doing the photos! Finally, my photography might have some commercial value after all.
Photos tomorrow!
Photos tomorrow!
Interesting reads
Labels: mixed, observations, personal, photography




