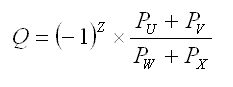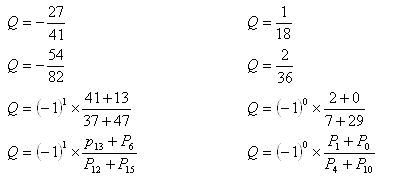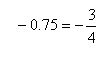Zhuk Cong Yup Si Fat

Zhuk chong yup si fat - catch a worm and put it up the anus (Cantonese); analogous to the phrase "shooting oneself in the foot"


I seem to be persistently creating confusion regarding my sexual orientation. Here is a list of potentially misleading things I’ve done over the past few months.

Experimented with nail buffing, and found that I liked the shine.

Used a cool pink colour scheme for my blog. (Pink will be back when blue goes off on a holiday)

Used the MSN nick “if only I had slimmer legs, I could sit with my legs crossed more elegantly”.

Wrote an ambiguous story about someone kissing a man, which could easily be misinterpreted as me kissing a man.

My nail buffing essay got published in The Voice (a biannual publication of the Melbourne University Overseas Student Union)

My nail buffing essay will be published in the International Engineering Student Society newsletter, entitled something like “Experiments of a (Genderly) Confused Mind”.

To hopefully convince you that I’m still reasonably sure of myself, here is a sample of porn. She’s not properly naked in the picture, to protect your innocent minds. You don’t want to know what sort of things lurks under those clothes between her legs. You really wouldn’t want to know.


Wah, leng lui, please keep your clothes on.

My silly nail polishing essay made it to publication. Twice over. With no effort on my part. A friend with tendrils reaching deep into the MUOSS power circle needed material for the magazine, and he approached me to print that thing. My housemate Adrian who has his own set of tentacles groping at the IESS’s own Kremlin was requested to write something for publication. Being busy/lazy/can’t be bothered, he forwarded my essay instead.



End note:

I actually thought it would be amusing if I put a picture of a muscular yet ‘cute’ man instead of that Japanese girl in that picture, and add another item to my list above. But then, it would create even more confusion. This time around, prudence ruled.

The Kiss

An attempt at micro-fiction.

[May 29 edit: Note the disclaimer above- An attempt at micro-fiction. The contents below did not happen to me. I did not try to kiss a man while trying to promote motor racing. A revised version is in the works to avoid these stupid gender confusions, among other shortcomings.]

The Kiss

by Tan Yee Wei

“You free this Sunday night? The European Grand Prix will be on at 8.00,” I asked him.
“Will it be any good?” He may be a man, but he is not much into cars and motor sports. Unlike me.

“Yes lah. Otherwise I wouldn’t ask you right? Anyway, the qualifying format is now a single 1 lap session, and BAR-Honda will be returning to racing. Circuit should be interesting; some heavy braking and tricky chicanes to promote potential overtaking.”

“Ok ok, I trust you. Dinner before that?” he invited.
“Come over to my place, I’ve got some nice fish.”
“I’ll bring some fruits over. And…and ice cream.”
“Nice.”

I pulled him closer and hugged him. I kissed him on his lips; he opened his mouth slightly. A warm, humid, saliva-ish and distinctly oral-cavity smell came to my senses. Immediately after that, I was hit by a pungent and musty smell of decaying vegetation.

I pushed him away, repulsed by his bad breath. “Tiu nia seng! Never brush teeth is it?”
Quickly gathering myself, I tried to mend the situation. “Sorry… slight over-reaction.”

Bad breath is good for bursting bubbles.

~189 (+/- 3) words

End of the Age of Oil, part 2

End of the Age of Oil

Chapter 2:
Towards 'E'

And thus, in the first decade of the 21st century, a big ominous ‘E’ appeared on the great petrol tank in the ground. Slowly, it became obvious to some that there will be changes to everyone’s lifestyles when the petroleum is finally depleted. Air conditioners run on electric power generated by burning natural gas. Air conditioners are shrouded in plastic, a petroleum by-product. The manufacture of automobiles require a tremendous amount of energy for the cutting, deforming, welding, transportation, painting, heat treating. To say nothing of running the said automobiles.

Without oil, there will be no plastics, no natural gas, no petrol, no kerosene, no diesel fuel, no bitumen. With no plastics, there will be no televisions, ordinateurs, plastic food containers, PET drink bottles, hypodermic syringes. Without natural gas, petrol, kerosene and diesel, there will be no cheap, plentiful energy. With no cheap, plentiful energy, it will be impossible to manufacture automobiles and air-conditioners, operate computers and televisions, run cars and aeroplanes.

More critically, farming and food production of the era was chronically dependent on nitrogen fertilisers, derived from ammonia made from hydrogen extracted out of natural gas. With no oil and natural gas, it will be impossible to generate hydrogen at dirt-cheap price. Consequently, ammonia, nitric acid and ammonium nitrate will not be widely available, causing widespread food shortage in the short term. It was the opinion of some learned individuals that without the aid of fertilisers and diesel powered equipment, food production would decrease by a massive 70%.

With these realisations, the enlightened few came to a collective gasp, followed immediately by “oh, shit!” The transition from a lifestyle of luxury and convenience to the post-oil age will not be an easy one. Whoever held control over the last remaining oil fields would hold power as long as those oil fields remain in working order.

Consequently, the first two decades of the 21st century were marked by a progressively vicious scramble for oil fields. The United States of America made the first move in 2003. Under the dubious pretext of anti-terrorism and liberation, it occupied the state of Iraq, gaining control over Iraqi oil reserve. Deciding to secure their own trophy oil-tanks before the reservoirs were all dominated by the United States, various other players joined the rush for The Last Droplets of Recoverable Oil. The European Federation, China and Russia used their own methods to acquire fresh fields in the Artic Circle, the Pacific Rim and Central Asia. Much to the delight and glee of spectators, the United States discovered at great surprise and expense that the purportedly rich oil fields in Antarctica were already empty.

While there was a frenzied rush for oil, there were also parallel efforts to prepare for the day when fossil fuel supplies were exhausted. Alternative sources of energy were investigated, with great strides made in hydro, tidal, wind, solar, fusion and fission power generation systems. More radical propositions include giant orbiting solar collectors and distributed fusion power generation. Meanwhile, the manufacturing and consumer products industries were preoccupied with developing plastic substitutes and technologies for manufacture of plastics from plant oils. However, this was assuming that there will be fertiliser substitutes to nourish these plants for their oils. One avenue was the use of engineered biological agents to produce the required products for fertiliser manufacture; another was by means of synthesis. Both required large amounts of energy, and thus everything hinged on the success of finding alternate energy sources.

With the rush for The Last Droplets of Recoverable Oil, developments in technologies to wean off society’s addiction to fossil fuels, the developed world marched on towards the great big ‘E’ for empty.


*ordinateur - computer (French)


Read Chapter 1

Autumn sunset photographs

The colours looked promising- freshly fallen autumn leaves, refreshingly green grass, splashes of golden sunset light.

The tree-lined central dividing strip on one of the roads below my apartment was precisely that- promising.

Quickly borrowing a digital camera, I went outside for some fun. Had to be fast- meteorological conditions can change at the drop of a hat, especially when the sun is setting, colours shift from yellow to orange to red while dimming rapidly.

[Click on images for large size photographs]

An ant's view of the situation



Autumn sunset

A partial list of my favourite books

“QED: the strange theory of light and matter”- Richard Feynman
A brilliant transcript of Feynman's QED series of public lectures, it is a must read for anyone interested in non-classical physics. Especially useful as a stepping stone to more detailed readings in quantum physics.


“Sophie’s World”- Jostein Gaarder
An excellent introduction to the history of Western philosophy, with a particularly unique storyline. Unfortunately, the plot sort of falls apart right at the end of the book, but it is of no real consequence; the material has already been presented.


“Prime Obsession: Bernhard Riemann and the greatest unsolved problem in mathematics”- John Derbyshire
Designed with the layperson in mind, but presenting advanced material in number theory. Done in two parallel threads of history and mathematics, it does more than introduce the Riemann Hypothesis and the Zeta function- it builds mathematics up from the ground up for the lay reader with lots of slightly unrelated topics to give the reader a taste of mathematics [1] and builds a very comprehensive biography of Riemann with snippets of details about the people around him and other interesting characters.


“Animal Farm”- George Orwell
A classical satire of dictatorship written in an engaging manner. The following elements are present but not explicitly stated: coup d’état, foreign policy, secret police, exploitation, (white and black) propaganda & communism. Not a bad partial list for such a short book. Mildly depressing plot, but still definitely worth the sadness.


Notes:

[1] The author’s notes from 1 all the way to 140 are definitely worth reading.
[2] I will also add this to my sidebar.
[3] Enough notes!

Constructing rational numbers using zeroes, ones, and prime numbers

[Another mathematics intensive post. Knowledge of lower-secondary mathematics assumed]

Assuming the Goldbach Conjecture is true,



Where Q is any rational number
Z = 0, 1
PN is the N-th prime number, P0 defined as zero.


The Strong Goldbach Conjecture (as re-expressed by Euler) asserts that any even number n >4 can be expressed as a sum of 2 primes. [1] Taking advantage of this statement, if we see an odd number in the numerator or denominator, we can simultaneously multiply them by 2, thus making them both even.

As an illustration, I will reconstruct the following rational number using the procedure highlighted above:



While the Goldbach Conjecture has not been proven since its birth in June 1742, various proofs have demonstrated that the conjecture is valid for small numbers. The latest estimate of this bound is 2 x 10^17 (5th February 2005). [1]

Of course, rational numbers could be simply constructed by taking the quotients of two natural numbers and adding a ‘–’ sign if necessary. For example:



That’s a little boring isn’t it?


References:
[1] Eric W. Weisstein. "Goldbach Conjecture." From MathWorld--A Wolfram Web Resource.

Star Wars Episod II and trigonometry

Of these 2, trigonometry is definitely more interesting.


On Sunday, the second episode of Star Wars was aired on free TV. I was extremely glad I did not bother to pay good money to watch it in the cinema, nor purchase any optical disc (pirated or otherwise) of the said production, nor spend precious time watching the entire film.

The actor for playing the role of Anakin Skywalker was terribly stilted. There were also several clichéd scenes that I thought Lucas should have done without. In a mid-air chase scene, Anakin told his sifu, “Now if you’d excuse me…” and promptly jumped out of the vehicle. The sifu mumbled to himself (and presumably the easily humoured audience), “I hate it when he does that.”

I stopped watching as soon as I was done with dinner. In my defence, I don’t intentionally eat in front of the TV; its just that the living area is in the same room as the dining area AND kitchen. It is plenty of space for 2 students, and not designed for a family with 4 young children.

Back to Star Wars. It appears that almost all vehicular propulsion systems in Star Wars have a certain signature note. This is particularly noticible in the smaller contraptions such as Pod Racers and the vehicle from which stiff Anakin disembarked from.

The signature sound in question consists of a moderate-pitched hum that gets louder and softer in a low frequency.

To try making this sound, start humming. Now, make your humming louder, then soft, then loud, then soft…in a consistent, periodic fashion. (Make sure the pitch does not change) Probably the only difference you will notice is that your hums go up and down much, much slower than what the film shows.

[The following material can get a little intense for individuals who are not mathematically inclined. Knowledge in SPM / O-Level modern mathematics expected.]

Curious about this phenomena, I did some ‘back-of-the-envelope’ calculations by banging some short equations into my favourite GUI (graphic user interface) mathematics problem solver- MathCad.

These are the equations and the corresponding plot:

W1:=200
A1:=5

W2:=201
A2:=6

x(t):=A1*sin(W2*t) + A2*sin(W2*t)
y(t):= cos[(W1-W2)*t]

W is the frequency of oscillation, and A is the corresponding amplitude.


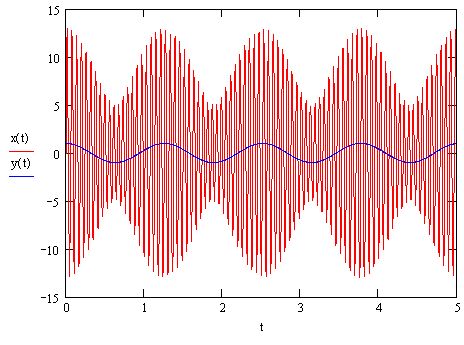The blue line of y(t) is to illustrate the frequency of amplitude change


Combining 2 separate sinusoids of frequencies 200 and 201 yields a signal of frequency between 200 and 201, and which has an amplitude which goes up and down with a frequency of (201-200) = 1.

This can be easily derived from trigonometric identities (which I did not go through).


And now, we return to the fictitious Star Wars propulsion systems. The hum is audible, and assuming it hums at the musical note of C, it will be at 440 Hz. The amplitude changes at a rate of about 3 Hz. Reconstructing the original signals that generated this signature sound, we can guess that it is of the form:

W1:=441 * 2 pi
W2:=438 * 2 pi
x(t):=A1*sin(W2*t) + A2*sin(W2*t)



Okay, that’s enough ‘useful’ information for now. Back to work.

End of the Age of Oil, part 1

I appears that I can't really impose a blanket ban on writing for myself. While taking a break from deriving equations of motion, I started writing something and the exercise blew up. So here is part 1. Subsequent parts will come as and when i take these extended breaks.

End of the Age of Oil

Chapter 1:
The Decadence of the Average 20th Century Dweller of the Developed States

By 2050, almost all of the world’s petroleum reserves have been pumped dry. Energy reserves, accumulated over the preceding 400 million years, had been squandered in a short 200 years.

As early as the 20th century, a small proportion of the population was already aware of the adverse effects of pollution on the planet, and was doing what little they could to help. Some citizens of the planet participated in recycling programmes in hopes of reducing waste generation and resource consumption. A few corporate citizens did their part by making products from recycled materials, and making their products easily recycled. Environmentally friendly products were developed, but were used by few.

These good citizens were the minority rather than majority. Much of the developed world was in a state of high due capitalism and consumption, and was indulging in a lifestyle of plenty and wastefulness. Industrial firms would not have installed costly filtration devices in their smokestacks were it not for government regulations. Individuals were in a state of bliss, driving alone in their luxury cars, getting stuck in traffic snarls, leaving the air-conditioner on while no one was home, throwing out a perfectly working ordinateur every two or three years, cooking enough food for 3 meals and then throwing away the leftovers.

In hindsight, it should not come as any surprise when the big petrol tank in the ground started showing a big ominous ‘E’. However, the ordinary 20th century dweller of the developed states was too absorbed in his quest for more material luxuries such as a bigger television, that he did not notice that the natural resources around him was finite in nature. The life of an average 20th century dweller was far too hectic to consider trivial limitations such as the environment and natural resources. On weekdays, he would be working in an office complex that had its air-conditioning turned too cold. On weekends, he would be preoccupied with enjoying life, after having the spent a good part of the waking week toiling for some promised material benefit that was to come at the end of the month.

Not realising that there was some ticking clock counting to zero, the average 20th century dweller of the developed states continued his decadent consumption. He went on driving alone in a big car, left the lights on upon leaving the room, watered his garden plants in the afternoon heat, and threw away his television for a splendid new plasma TV.


* ordinateur - computer (French)

Be Right Back

I will be writing significantly less frequently until the end of the month. After that, I will be back to my usual self. Ironically, that is when my exam study-break starts, on the first week of June, and then 4 exam papers over the subsequent 3 weeks.

In the shorter term, I will be facing many challenges.

Completed	Item	Due date
30 %	Mechanical Vibrations assignment	16 May
5 %	Engine knock lab report	18 May
5 %	Control Systems assignment2	27 May
40 %	Solid Mechanics assignment	27 May
0 %	Major Project progress report 1	27 May
0 %	Professional Practice summary of seminar lectures	30 May

There are also rumours of an additional Thermodynamics assignment. Drat.

This list does not look as scary as one I constructed a year ago. That particular semester involved many subjects, and most had a few lab sessions and their own assignments. At one point, I had 13 (smallish) documents that were due.


brb (circa 1st June)

Sunsets of Melbourne

I was walking home from the university this evening and noticed the pretty sunset performance. Straight ahead along the road was the city centre, with tall, occasionally majestic buildings sheathed in glass and aluminium. The upper halves of these buildings were illuminated yellow by the setting sun, as if they had each been recently drizzled with a generous ladle of thick, golden and overly sweet syrup.

Melbourne had always been generous with the sunrise and sunset light shows. I attribute this to the generally low humidity found here, reducing the moisture in the atmosphere that might absorb any light. The sunset colours progress from yellow to orange, sometimes even to an intense shade or orange-pink, illuminating progressively higher parts of buildings, lower buildings blotting out the sun as the horizon races up to catch the sun.

When I got back home, the sun was still doing its thing, illuminating the outside in increasingly redder hues. Nearer to the time of sunset, I went outside my balcony for a good look. Over the western horizon, a slight sprinkling of clouds was doing wonders for the scenery. On various boundaries of these tufts of suspended water droplets, light was reflected and diffused, creating an amazing highlight of gold in a sky lit by yellow.

Here is a photograph from 31st of March 2004. Can you find the helicopter?

click to view large iamge

How convenient it would be if I had a digital camera. As a substitute, I used a few frames of photographic film in my trusted Olympus iS-1000.

Post race evaluation of pre-Spanish GP report

The objective of this post is to assess the accuracy of some estimations and predictions made before the race.

Drat…now that we are getting to the accuracy assessment part, it appears that there is not much to evaluate. While processed data was abundant in supply, there were few (if any) predictions and estimates.

Mark Webber did indeed attempt run on a low fuel strategy, as revealed later. The initial plan was to refuel 3 times. However, this plan could not work due to the following reasons:

Mark failed to gain pole position.
Mark was out-accelerated by Fernando Alonso in the drag down to the first corner during the start (this has been attributed to software issues and lack of power by various speculators).
Mark was overtaken aggressively by Ralf Schumacher.

Trapped behind Ralf Schumacher, Mark could not put in the fast laps that his light-weight car would allow him to. The strategy was then changed to a 2 stop strategy, with the car pitting early and filling up on fuel, running a long second stint before the last stop.

Future pre-race reports might take extra factors into considerations:
Acceleration from standing start, affected by track grip, tyre performance, fuel load, speculated engine power and chassis performance.
Projected spread during initial stint due to differences in lap times and being held back by slightly slower cars.
Tyre wear.

Data analysis will hopefully include:
Q1 lap times to consider unfavourable track conditions (case in point: Juan Pablo Montoya).
Sector times to evaluate the effect of fuel load on performance at each sector.



ps- I am aware that most people don't give a damn about motorsports. These Formula 1 related discussions will be limited to 2 each race, races being spaced on average once every fortnight.

Work? Haha...you must be joking... :-(

It’s another of those weekends- there’s work to be done, but none actually done.

The Spanish F1 Grand Prix is due to start very soon has started, but the telecast on free Australian television will be 2 hours late.

I’ve taken the trouble to analyse the qualifying performance of the drivers, and below is a brief summary of my observations.


Pre-Spanish Grand-Prix Report- start line fuel loads

In the first qualifying run (Q1), drivers run on minimum fuel loads, while the second run (Q2) is conducted immediately before the race, and fuel tanks cannot be topped before the race.

Assuming that the drivers do their best on Q1 and Q2, the time difference between Q1 and Q2 will be indicative of the fuel load they are using to start the race. The start position is determined by adding their lap times in Q1 and Q2.

Below is a chart of the time difference (in seconds) between Q2 and Q1. Drivers are arranged by starting order.

If a car has more fuel, it can run longer before having to pit and refuel.


It appears that Kimi, Fernando, Ralf, Jarno and Michael are reasonably well matched in this respect. It is possible that Mark had tried to do a fast Q2 using less fuel, but messed it up and will start the race starting behind Kimi. Juan did not race for the past 2 races, and thus started Q1 very early in the session when the track was comparatively slippery. Hence, it is difficult to judge his car’s initial fuel load.

Rubens and Nick did not run on Q2, and consequently will be starting from the last positions.


ps- a post-race report will inform you on the (in)accuracies here.

How I take my coffee at home

Immediately after being roused in an unceremonious fashion by my loud clock-radio, I usually head straight for the toilet. After that, in a semi-conscious state and in my pyjamas, I would make my way downstairs.

“Morning Ma”, I greet my mother in a mumble. Occasionally, she would try to jump-start my consciousness by making me enunciate the words clearly, although it’s becoming increasingly rare lately. I think she has given up on that.

After obtaining a cup from the cup rack, I fill it with two centimetres of water. With the press of a button, levers unhook the microwave oven’s door. As internal springs propel it open, a dim yellow light illuminates the stark stainless steel interior. My cup, with its 2cm of water, is placed in the middle of the oven’s circular ceramic dish.

Due to my slight preference for symmetry, it had become a habit to put the cup right in the middle of the rotating circular dish. It might also be caused by an article I read reporting that the heating effect of microwave ovens is most prominent in the middle.

Having inserted my cup, I closed the oven’s door with a thump as its sprung levers catch to lock the door and the lamp extinguishes. After 3 button presses in rapid succession, the lamp is on again, accompanied by the dish slowly rotating in the stainless steel chamber and a persistent hum of cooling fans.

It is another habit of mine to heat my coffee-water for one minute and ten seconds. It just happens that in one minute, the cup ends up facing the other way, such that I would have to reach round the cup to find its handle. However, 70 seconds is just nice for the cup to face forward again, saving me from having to grope about or to force the turntable to rotate around.

In a large cup, add one teaspoonful of instant coffee, three quarters of a teaspoon of sugar, 2cm of hot water, and top up with cold milk. My day starts here.

Buzz Buzz Buzz!

After an extended leave of five months from narrative fiction, I decided to do a short story. It turns out that I’ve been away for far too long. Instead of reasonably pleasant and varied sentences, they now come as terse, monotonous and one dimensional fragments that resemble my works 2 years ago. While these simple sentences work wonderfully in explaining technical material (I’ve been working exclusively on automotive engines for 3 months during my holidays), they absolutely suck when applied to narration.



After half a day of overly challenging lectures, I finally arrived at the front of my apartment building. Interrupting an invisible beam of infra-red light, I prompted an automated glass pane to slide aside, allowing me entry into the apartment’s tiny front area.

Here in this restricted space, an array of 32 aluminium faced mail boxes completely covered one side wall. On the opposing wall were a magnetic card reader and an intercom device. Another sliding glass door allowed restricted access into the apartments. Without a magnetic card or an explicit ‘open’ command from an occupant, the door will not budge.

I fumbled in my wallet for my magnetic card. Drat! Where was it? After searching through the various card pockets of my wallet, I finally concluded that it was not here. Using the intercom device, I rang a friend’s apartment unit. Fortunately, he was home to remotely open the second set of doors.

The rest of the day progressed without incident, being a normal day of web surfing, blog writing, online chatting and little real work. My day ended at 1.00am when I decided it was time to sleep.


Like a tiny but persistent itch, a buzzing sound penetrated the dark mist of my sleep to pierce into my consciousness. Initially, it was not a significant disturbance, only barely noticeable and easily ignored. Gradually, this violation began to make itself felt by breaching more of my hazy cloak of sleep.

As a reflex action, I tried to ignore it, but it was becoming increasingly difficult. By now, I was conscious enough to realise that it was my intercom buzzing rudely. Not thinking quite rationally, I continued to lie, hoping the person might go away. Two more impertinent buzzes later it became apparent that the early-morning ringer was not intent on leaving.

Finally rousing to answer the call, I realised that it was barely 4.30 in the morning. The caller better had a good reason to wake me up!

Picking up the intercom receiver, I listened without making a sound. The other side would not be aware that I was tuning in unless I made a sound that would be transmitted. I heard a man’s voice, slurred and mumbling. He appeared to be begging for entry.

“Drunk idiot,” I concluded.

He had stopped buzzing my intercom. Either he had given up, or realised that he had been pushing at the wrong key.

I went back to sleep.

At a more proper 10am, I left my apartment unit to head for the university. Descending in the lift, I contemplated the events earlier in the morning. I was particularly miffed at being roused for no real reason, at 4.30 too.

With a slight shudder and a few creaks from the aged Otis mechanism, the lift came to a halt. After a short pause, the doors slid open, revealing a busy scene.

Outside the apartment, several police cars were perked with their blue lights still flashing. A few officers were crowded about the apartment entry area, pointing and taking notes. A police photographer was snapping images of the intercom, the glass panes and the floor tiles.

As I went through the area, I noticed there were numerous bloodstains splattered on various surfaces. There was a substantial puddle of dried blood on the floor just below the mailboxes, and various smaller but nonetheless disturbing smears and marks on the glass doors and walls.

On the intercom’s panel, I saw several bloodstained fingerprints. In particular, my apartment unit’s button was smeared in many overlapping layers of bloodied prints. “Oh shit…what have I done?”

“Excuse me sir. Which apartment are you from?” a youngish police officer stepped up to me. Without a word, I pointed at the bloodiest intercom button. “What happened?” “Someone died here. We would like you to help with ongoing investigations.”



The above narration (up to the lift descend) is based on my personal experiences. Someone actually rang at 4.30am. Fortunately, there was no blood the subsequent morning.

More advertisement, among other things

I’ve got another blog here. It’s a joint effort between Vic and me. Topics of discussion range from theoretical to applied science. While many of the titles are horribly intimidating, some of the materials are actually quite friendly to read.

Indirect perception of time-derivatives
Some thoughts on the 4d problem
Automotive braking loads and the occupants' perception of it
On postulates of quantum physics
Real materials as opposed to rigid bodies
On Entropy
Rigid Bodies violate Special Relativity

We go a long way back in terms of joint writing projects. We started out in a rather impromptu fashion in August 2002*, when we wrote a short story (at a friend’s expense) in 20 minutes. More stories followed. Initially, the works were based on common jokes among the readers. Later stories incorporated more of our own (toilet) humour. Compositions began to show some semblance of plot development.

We moved away from writing for a very small niche market of about 10 to write general material for anyone who might be interested. In February 2003, a public portfolio was created at writing.com. With university upon us, there was significantly less time to write fiction. Several were started, but sputtered and stalled due to lack of development time.



Personally, my favourite method to introduce an unfamiliar city was by its transportation networks (maps easily obtained via the web). I can tell you that the Kakhovskaya line is the shortest line in the Moscow Metro network, spanning 3 stations. The Kakhovskaya is used to connect two parallel lines, the Zamoskvoretskaya and Serpukhovsko-Timiryazevskaya lines. To visit the Kremlin, stop at the Kitay Gorod or Teatralnaya stations.

Knowledge about the transportation details seem to convince the reader that the setting IS Moscow instead of some imaginary city pretending to be Moscow (minus the Moscow River and its tributary the Yauzza River.


* Prior to this, I had never written anything on a voluntary basis.