The JFE 8555 problem revisited- digital roots
Note: Familiarity of the concept of congruence is expected. Failing that, a concise introduction can be found here.
A rethink of the original problem has prompted a much neater (although not necessarily any easier to read) and a more general solution.
To generalise the situation, the number involved will be written as abcd with each letter representing one digit. This number abcd can be in any base n. For sake of simplicity this number is represented with only 4 digits, but can be extended to as many digits as desired.
Separating the digits of abcd:
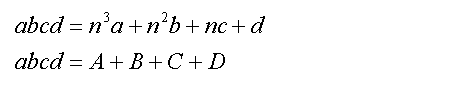
Equations (1)
Remember that the notation is generalised for any base-n, hence the powers of n are used instead of thousands, hundreds and tens as used in base-10.
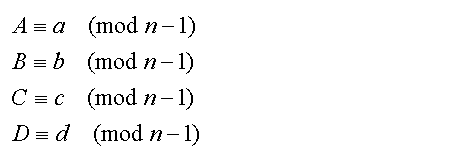
Equations (2)
Equations 2 are valid statements. To illustrate, we will use n=10 with B:
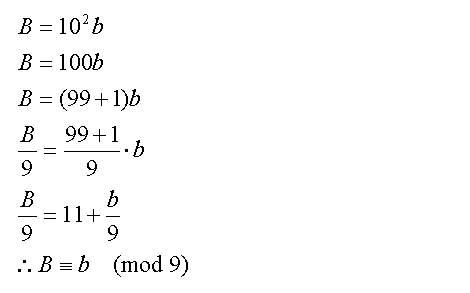
Equations (3)
Now, on to a bit on the properties of congruence:
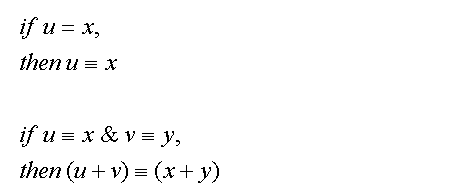
Equations (4)
Applying these rules to the number abcd:
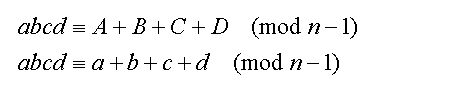
Equations (5)
Now, suppose we cluster the digits into groups of two and summing the elements in each group. This is illustrated using abcd= 1534, base-10.
5734
5+7; 3+4
12; 7
1+2;7
3;7
3+7
10
1+0
1
The digital root of 5734 is 1.
Returning to the general case,
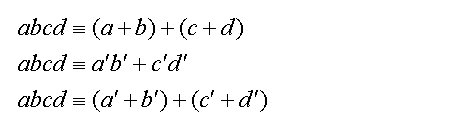
Equations (6)
The last step taken is exactly the same those presented in equations (5). Continuing on, the sum of the digits in each bracket is only one digit (for all cases of n greater than 2, the trivial case). This is because both digits are smaller than n, and the sum of two digits, both smaller than n, result in number than when its digits are added, result only in one digit.
Illustrating using base-10, the sum of 2 digits: 9 and 9:
9+9 = 18
1 + 8 = 9
At the limit, n (in this case, n=10) digits may be added and the result remains as one digit:
9+9+…+9=90
9+0=9
To continue from equations (6), the sums of the bracketed numbers result only in one digit each:
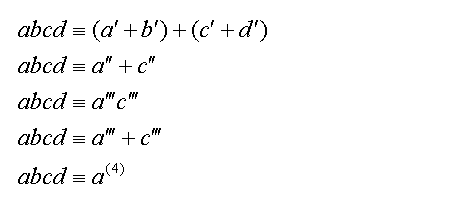
Equations (7)
In equations 7, the digits are further added and finally reduced to the resultant digital root a''''.
Now, to show that the grouping order of the addition operations do not matter, the grouping of ab and cd will now be reordered to abc and d.
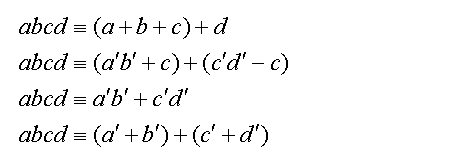
Equations (8)
Which gives the same result as the grouping of ab and cd.
In conclusion, the digital root of a number in base-n is congruent to the number, mod n-1. The digital root is independent on the summation order of digits.
End note: Now, the interesting question is, who would read this? Yuan Harng, most probably. Michelle Chong, maybe. Everyone else just hits the big red x on the top right of the window.
So why did I do this? Because I needed a mental workout.
Mathematics
A rethink of the original problem has prompted a much neater (although not necessarily any easier to read) and a more general solution.
We will attempt to add the digits together in any arbitrary manner, repeating till we reach one digit.
35897
-> 3 + 5 + 8 + 9 + 7 = 32
-> 3 + 2 = 5
(35) + (897) = 932
-> 9 + 3 + 2 = 14
-> 1 + 4 = 5
(3+5) + (8 + 9) + 7 = (8) + (17) + 7
-> 8 + (1+7) + 7 = 8 + 8 + 7
-> 8 + 8 + 7 = 23
-> 2 + 3 = 5
3 + 58 + 97 = 158
-> 15 + 8 = 23
-> 2 + 3 = 5
The flabbergasted reader might want to try a few other addition combinations for amazement’s sake, and to show that the result is always 5.
To generalise the situation, the number involved will be written as abcd with each letter representing one digit. This number abcd can be in any base n. For sake of simplicity this number is represented with only 4 digits, but can be extended to as many digits as desired.
Separating the digits of abcd:
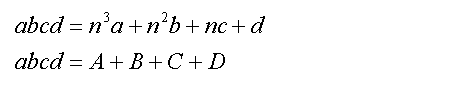
Equations (1)
Remember that the notation is generalised for any base-n, hence the powers of n are used instead of thousands, hundreds and tens as used in base-10.
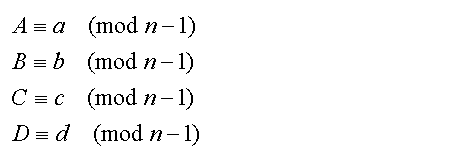
Equations (2)
Equations 2 are valid statements. To illustrate, we will use n=10 with B:
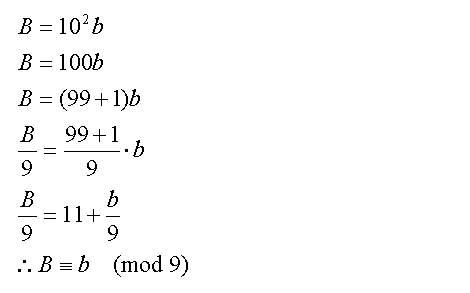
Equations (3)
Now, on to a bit on the properties of congruence:
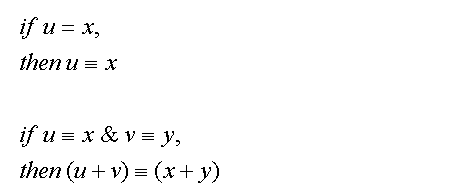
Equations (4)
Applying these rules to the number abcd:
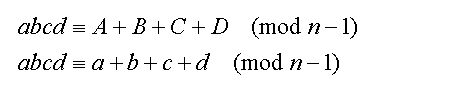
Equations (5)
Now, suppose we cluster the digits into groups of two and summing the elements in each group. This is illustrated using abcd= 1534, base-10.
5734
5+7; 3+4
12; 7
1+2;7
3;7
3+7
10
1+0
1
The digital root of 5734 is 1.
Returning to the general case,
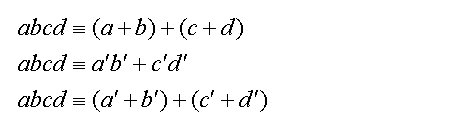
Equations (6)
The last step taken is exactly the same those presented in equations (5). Continuing on, the sum of the digits in each bracket is only one digit (for all cases of n greater than 2, the trivial case). This is because both digits are smaller than n, and the sum of two digits, both smaller than n, result in number than when its digits are added, result only in one digit.
Illustrating using base-10, the sum of 2 digits: 9 and 9:
9+9 = 18
1 + 8 = 9
At the limit, n (in this case, n=10) digits may be added and the result remains as one digit:
9+9+…+9=90
9+0=9
To continue from equations (6), the sums of the bracketed numbers result only in one digit each:
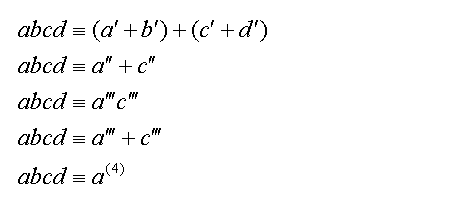
Equations (7)
In equations 7, the digits are further added and finally reduced to the resultant digital root a''''.
Now, to show that the grouping order of the addition operations do not matter, the grouping of ab and cd will now be reordered to abc and d.
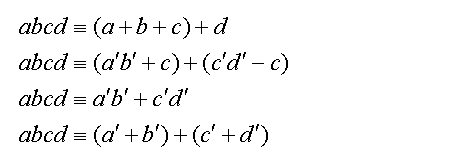
Equations (8)
Which gives the same result as the grouping of ab and cd.
In conclusion, the digital root of a number in base-n is congruent to the number, mod n-1. The digital root is independent on the summation order of digits.
End note: Now, the interesting question is, who would read this? Yuan Harng, most probably. Michelle Chong, maybe. Everyone else just hits the big red x on the top right of the window.
So why did I do this? Because I needed a mental workout.
Mathematics
Labels: mathematics, milestones and such, number theory

<< Home