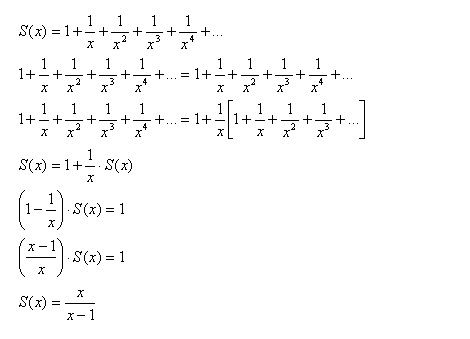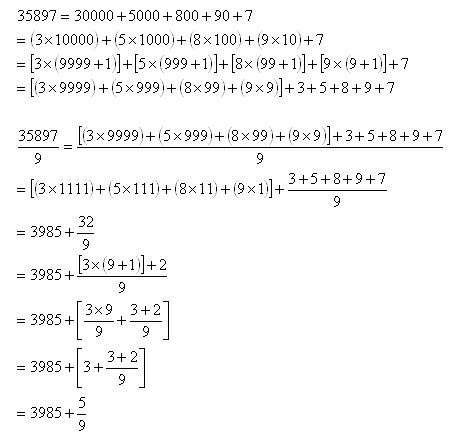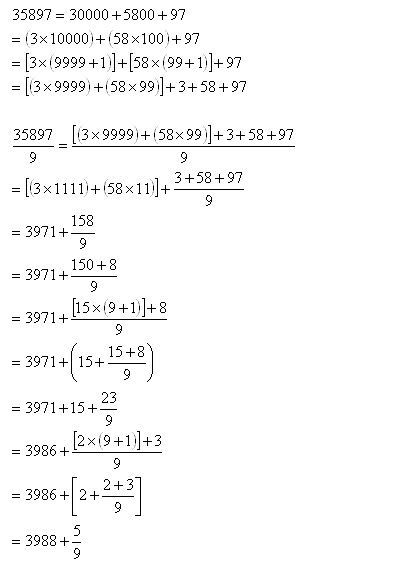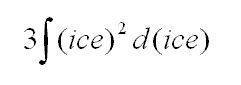Kongkek faraj...BM saya menyedut

Seperti yang dijanjikan semalam, hari ini saya akan membelog dengan Bahasa Malaysia bersama dengan banyak orang lain. Mula-mula, saya fakir saya akan menulis karangan ini dengan Bahasa Ingerris, dan menterjemahkan kepada Bahasa Malaysia. Tidak susahlah, kerana terdapat banyak perkataan BM yang berasal dari Inggeris.

Strategi penulisan ini senang- saya akan menggunakan banyak perkataan Inggeris yang bombastik, seperti bombastik, innovatif, inisiatif, integerasi, bajet, iterasi dan posisi. Lepas tu, saya akan ejakan dengan ejaan BM. Ada kemungkinan terdapat beberapa perkataan yang tidak sah, tetapi banyak buku revisi PMR dan SPM sering mengguna perkataan bombastik untuk meningkatkan imeg buku tersebut.

Selepas sedikit pemikiran, nampaknya strategi ini tidak baik sangat. Ini hanya akan menindaskan BM. Akan tetapi, saya rasa saya telah menulis terlalu banyak, dan penterjemahan kepada BM akan menjadi kesakitan dalam punggung. Saya akan berhenti di sini.

Kongkek faraj...BM saya menyedut.

Kod sumber Bahasa Inggeris di bawah.

As promised along with many other people, I will be making an entry in BM for today. Initially, I thought I would write the entire paragraph in English, then translate it to BM. I should not be too difficult, since many BM words are derived from English words.

I would only need to use many bombastic sounding English words like bombastic, innovative, initiative, integration, budget, iteration, investigation and position. Then, I can simply spell them in a BM fashion, and viola! Of course, some might not be legit words, but then, revision books that try to portray an image of progressiveness tack on many English adjectives on their covers anyway.

After some thought , it seems to be a bad strategy that will do nothing more than insult a language. But then I think I have written too much and the translation will be a pain in the ass, so we will leave it as that.

Fuck chi bai...my BM sucks.

The English source code is available below.

Blogging in Malay, because everyone is doing it

Among my many traits, I am sometimes a weak minded person. Without a rational mind to think ideas through in an objective manner, I usually end up making weird choices.

I also have a strong inclination to be in the ‘in’ group. I have a tendency to do things just so I am not left out. Thus, I am an easy prey of mass hysteria.

As a consequence of the above two qualities, I am opinion-less like a hopeless strand of lalang in the brutal embrace of Katrina. If digital pets are the thing to have, you will see me with several of them beeping around my pockets.

As a direct effect of the above three attributes, I will be blogging in BM tomorrow (31 August). I am doing it because almost every other person is doing it. I want to be cool. I want to be accepted.


Do not take the above paragraphs seriously.

Since it’s our National Day tomorrow, since it would be interesting to write in Malay for a change, and since everyone else is doing it anyway, tomorrow’s entry will be in Malay.

My linguistic skills are not top notch. As such, do not expect anything of decent quality at all tomorrow.

How I got owned in a sparring match

Yesterday I went for a martial arts competition with the Melbourne University Karate Club (MUKC).

The competition was organised by the Lion Bushido Karate Academy, and subject to their rules. A few remarkable points about their sparring rules:

Light contact
Minimal contact to head
Kicks must not follow through (basically a fast, light tap instead of a friendly bang)
No axe/chopping kicks [wtf...]
No spinning kicks (reverse swing/ hook kick/ spinning hook) [WTF!!!]

I woke up at 7.45 on a Sunday morning, took a long tram ride to St Kilda, met with other team members and went in one of the guy’s car. The venue was a long way away from Melbourne city centre.

7.45am!

At about 12 or 1pm, the chief instructor from MUKC (who was also helping with refereeing and judging) approached me and asked me into the officials (and competitors) only area. It seems they were short on referees and would need me to be the corner judge for a sparring event. Something like they were temporarily short of black belts to judge. What he probably meant was that most of the black belt holders floating about the venue have not had their uniform on yet, and I’m the only one he knows that looked presentable.

Like a fish suddenly yanked out of the water, I was quite surprise at the abrupt turn of events.

“Huh? Corner judge?”
“Don’t worry, it’s not difficult.”
“But I don’t any have experience in this.”
“You just subjectively judge which competitor fights better. And give the winner 10, and the loser 8 or 9. If they are evenly matched give them both 10s”

I know it’s damn easy to judge. I could just give the Red competitor the win by a 10-9 margin every time, and no one would know. It’s just an ethics problem. 3 judges give a score, and the numbers are tallied to determine the winner. What if it is so evenly matched that my vote will be the swing vote? Then my pseudo-random function will determine the outcome of the competition. Which is not all that good, really. When they say ‘may the best (wo)man win’ (cliché), it actually means that the best person wins. This is a competition, not a casino.

Attempting to judge fairly is not easy. If the mind strays, one must yell at it to get back here. Also, a conscious attempt must be made to pay equal attention to both competitors. I sort of learned the mental approaches to judging along the way, so I can only hope that I did not swing the vote unfairly in the first couple of matches.

Much later in the day, at about 3.30pm, I was due for my sparring event. I lost so badly that the magnitude of the loss itself was an eye-opener. Cliché: you learn something new everyday.

From past experience, if anyone got too near for comfort and started punching, I can simply unwind with a back-thrust. The resulting momentum transfer would ensure that they no longer remain near, and probably think twice about coming near again.

Unfortunately, this is a ‘friendly’, no-contact sparring. It’s impossible to impart any momentum without decent contact, so I was flooded with punches. It was not funny.

There were a few satisfying turning kick head shots, but I was mostly submerged in punches anyway. The punches don’t really hurt, but they are scored. So they do hurt a lot actually, in a different way.

And then reverse swing and chopping kicks allowed. That was a major avenue of technical tricks closed off.

In hindsight (cliché: hindsight has 20/20 vision), it should have been ok to tackle. If the short range attacks kept coming, it would have been possible to slide backwards with a turning kick, another 2 steps back, a side kick to stop progress, advance forward to counter attack.

Hindsight...I can only blame my lack of composure and quick thinking. That’s inexperience for you.



Personal

The infinite geometric series and inflation

Assumed knowledge: elementary manipulation of equations (lower secondary mathematics)
Difficulty: 3/5
Tedium: 3.5/5
Insight: 3/5


Table of contents:
Amendments
An infinite amount of money
The infinite geometric series
Inflation and the present value of future cash
Connecting the two ideas
Which prize to choose?
Cite this article
Appendix: geometric proof of S(2)=2



Amendments
__earth has pointed out a flaw in my economics:

actually, inflation and present/future value are two different but related idea.

What you've explained is present/future value of money. The rate is not inflation but instead, it's nominal interest rate.

In fact, in economics, when real rate is r and nominal rate's i with inflation's pi, the equation is approximately,

r = i - pi.

But then, you could assume real interest rate is zero and hence nominal insterest rate is equal to inflation.

JFE 8555 has highlighted an assumption that was not declared:

[I'll take] 25 bucks now, coz i may not see tomorrow.

The assumption is that $1 in your great-great-grandchild's wallet has the same value as the present value of that same dollar now, in your hand.



An infinite amount of money
Suppose you have been awarded a prize for being the tidiest person in your school/institute/company. For your prize, you can pick one of the following choices:
$25 now
$1 annually, indefinitely.

By now, alarm bells should be ringing in your head. Infinity?!
We’ll have try to make some sense of this mess.



The infinite geometric series
Consider the following series:



Each subsequent term in S(2) is half of the previous term. We can have S(3), and that would give us a series that has each subsequent term as one third of the previous term.

To calculate S(2), it would entail adding an infinite number of terms, and hope that it does not blow up in our faces. Observe:



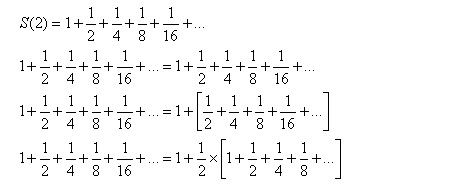
I’ve written that S(2) is equal to S(2), which makes perfect sense. Subsequently, I have separated the first term from the others by the use of a bracket.

I then multiplied each term in the bracket by 2, and divided them all by 2. Nothing has changed- its only multiplication by one.

This is the elegant bit: the infinite geometric is now expressed as 1 + half of itself.



Repeating the same exercise for a general S(x):





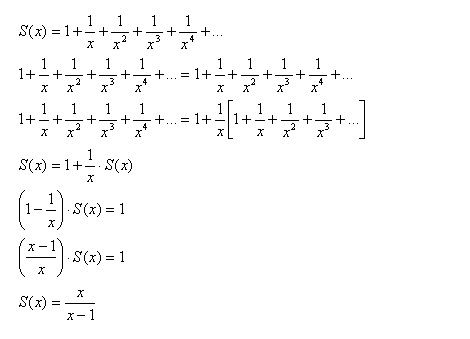Inflation and the present value of future cash

In the economy we are currently stuck in, there is a trend of increasing prices. Often, $1 will not buy you the same amount of goods $1 did back in ‘those days’. Suppose we are in a very messed up economy which sees an inflation rate of 100%- every year, prices increase by 100%. A bar of chocolate which costs $10 today will cost $20 next year. In other words, today, $10 will buy one bar of chocolate. Next year, $10 will only buy you half a bar. Another year later, the chocolate price will have doubled yet again to $40 a bar. $10 can only get you a quarter bar.

This brings us to the problem of concept of net present value. Suppose you know that you will obtain $10 in 2 years time. You would be able to buy a quarter bar of a chocolate.

Today, the same quarter bar of chocolate will cost you $2.5. Thus, the value of $10 in 2 years time is $2.5 now, for a case of 100% inflation.

With a more sedentary case of 5% inflation would mean prices go up by 5% per year. What used to cost $10 would cost $10.50 the next year, and $11.025 the subsequent year.

In 2 years time, when the price of a bar of chocolate is $11.025, $10 can only buy you 0.907 of a bar. Currently, 0.907 of a bar would cost 0.907 x $10 = $9.07. Thus, the value of $10 in 2 years time is $9.07 now, for a case of 5% inflation.



Connecting the two ideas

Having seen the infinite geometric series and the present value of future cash, we can connect the ideas to the concept of indefinite payments (as presented as an option in the prize).

Suppose you are in a horrible economy where the inflation rate is 100%. Every year, the price of goods double; every year, the value of money halves.

In other words, $1 next year is can only buy you as much as $0.50 now. $1 two years later is only equivalent to $0.25 now. $1 three years later is only $(1/8) now.

Now, we get paid $1 every year, indefinitely. Taking the net present value, we calculate how much each $1 in the future would be worth now. It turns out to be the infinite geometric series S(2):



Note that because we are having an inflation of 100%, prices double every year. This doubling is reflected in the 2 found in S(2).

In an economy with 5% inflation, every year, prices are 105% that of last year. In this case, the net present value of the indefinite $1 annually is S(1.05).



In general, the net present value of an indefinite annual payment of $1 (starting this year), in an economy with inflation of i, can be expressed as S(1+i).



Which prize to choose?

The choice offered is either $25 now, or $1 annually.

Here, we make a drastic simplification: the economy’s inflation stays constant indefinitely.

At what inflation rate does the choice become irrelavent- the net present value of the payments ($1 annually) equal to the current payment ($25)?



When the inflation rate is at 4.1666%, there is no monetary gain by choosing one over the other. If the inflation is greater than 4.16667%, then it would make sense to choose the $25 now rather than $1 every year. Just to highlight the point, 100% inflation will give a net present value of only $2, definitely less than $25.

If, on the other hand, inflation is less than 4.16667%, it would make sense to choose the annual payments. For example, if there was no inflation, the present value of every $1 in the future stays at $1, and the indefinite sum would explode into an infinite amount of money.

The choice is thus dependent on the constant predicted inflation rate for the economy.



Cite this article

Tan Yee Wei(2005), "The infinite geometric series and inflation", from "Snippets of This and That"
http://tanyeewei.blogspot.com/2005/08/infinite-geometric-series-and.html



Appendix: geometric proof that S(2)=2
Proof given by Lee Yuan Harng

This is a geometric proof of the following:



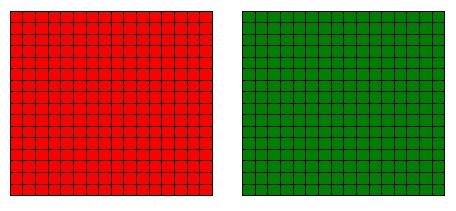
We first draw a square of size 1, as represented by the red square.
To add 1/2, we add the yellow rectangle, which is actually half a square.
To add 1/4, we add the grey square, which is actually a quarter of the red square, or half of the yellow rectangle.
To add 1/8, we add the green rectangle, which is half of the grey square.



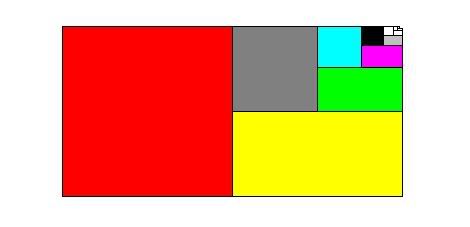
This addition goes on indefinitely, and each subsequent shape is exactly half of the previous shape.

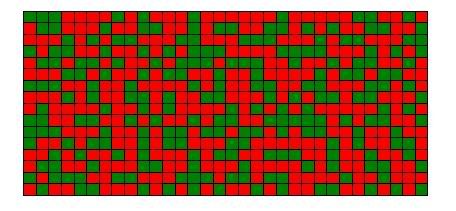
The first few terms in the infinite geometric series S(2) correspond to the red, yellow, grey, green, blue, fuchsia, black, silver elements.

All subsequent terms are small enough to be shoved into the white unfilled area at the top right corner. In earlier additions, each new term only occupied half of the existing unfilled area. When we only had the red square, the right side portion was unfilled. Adding the yellow rectangle only filled that space up by a half. The next addition, the grey square, only filled up the remaining space by a half, and so did the subsequent addition.

From another point of view, the unfilled space decays by a half for every new term added. At the limit, the space decays to an infinitesimal area of about zero. The filled space thus occupies 2 units.







Mathematics

The Red Army Through Snow

The theme of today’s photography session was red.

It was about 2pm, with direct, intense sunlight through the windows.

On impulse I splashed some milk onto the photography subject of the moment- a sparkling ruby of a strawberry. It was a bad idea- milk droplets clung onto the indentations of the berry, giving it an appearance of illness.

I gave up on that milk afflicted berry and grabbed a new one. This time, milk was poured into a wide plate before the berry placed into the puddle. A chilli was added later into the session.







The Red Army Through Snow

Click here for large size image
Click here for Deviant Art entry



The good thing about having a thin (1mm) film of milk in the plate was that milk diffuses light very well. As such, the original harsh glare of porcelain is completely diffused by the milk. Also, the milk has a slight pearlescent texture due to diffusion of light, and shadows appear to be a little warmer in hue.

Another interesting quality about milk arises from the fact that it is a liquid, and thus forms a perfectly smooth surface. Unfortunately, being liquid has a drawback in that it is subject to surface tension forces. A meniscus forms around anything that happens to be in contact with the liquid, thus the surface is not flat at the edges of the liquid body.

Upon loading the images onto my hard disc and opening the folder, I was confronted by this splash of red.





Click here for large size



Photography

Daft engineer jokes

Slightly past midnight and I was feeling a little empty inside. I need food.

As I spread the peanut butter onto my freshly toasted bread, the thick paste began to melt, and slowly seeped into the pores of the bread’s surface.

Adrian saw me preparing to eat, and he decided to have a supper of toasted bread too.

We I talked rubbish for a while before he turned serious.

“Hey, ask you something…”
“Mmm?” My mouth was full of toast and melting peanut butter.
“I’m designing a tank farm [for my project]. Where do you think the control room should go? Should it be near the loading area, the pumps or the tanks themselves?”

We discussed the various possible locations before implicitly agreeing that it should be located away from the tanks, pumps and loading point.

“Yea, just locate the control room remotely. Like put it in Bangkok or something…”
“Or I could say that since it doesn’t matter, I’ll design the control room as a submersible and put it underwater, offshore.”

I then made a suggestion:

[The following has been adapted to fit a text format]

Since you do not want the control room to be near the tanks, pumps nor loading point, you should aim to put the control room at a location that as equally apart from each facility.

The most obvious way to do this would be to arrange the tanks, pumps and loading point in a circle, and put the control room in the middle. The illustration shows the control room as the square in the centre of a circle of facilities. Clearly, this is an impractical arrangement.



The other solution would be to place the control room infinitely far away. This way, the distance to each of the tanks, pumps and loading point would be the same.




Personal

The JFE 8555 problem explained

Continuing from the previous entry:

We will attempt to add the digits together in any arbitrary manner, repeating till we reach one digit.

35897
-> 3 + 5 + 8 + 9 + 7 = 32
-> 3 + 2 = 5

(35) + (897) = 932
-> 9 + 3 + 2 = 14
-> 1 + 4 = 5

(3+5) + (8 + 9) + 7 = (8) + (17) + 7
-> 8 + (1+7) + 7 = 8 + 8 + 7
-> 8 + 8 + 7 = 23
-> 2 + 3 = 5

3 + 58 + 97 = 158
-> 15 + 8 = 23
-> 2 + 3 = 5

The flabbergasted reader might want to try a few other combinations for amazement’s sake, and to show that the result is always 5.

The key to unravelling this problem lies in the number 9. What is so special about this number?

We’ll first consider the numbers 10, 100 and 1000.
10 = 9 +1
100 = 99 + 1
1000 = 999 + 1

Divide the numbers by 9:



The interesting point about this division operation is that there is a remaining fraction 1/9.

The following example (using 35897) should make it obvious that this division by 9 is analogous to digit extraction where we extract digits out of a multi-digit number.



And out of this mess comes 5 as the numerator in the fraction.

So the above case was an illustration of
35897
3 + 5 + 8 + 9 + 7 = 32
-> 3 + 2 = 5


Can we do it for the following?
35897
3 + 58 + 97 = 158
-> 15 + 8 = 23
-> 2 + 3 = 5

This time, the digits have been arbitrarily condensed into groups.



Again, 5 appears at the end of the digit summation operation. 5 always appears, because the digit summation operation is simply showing part of the divide by 9 process. And, 35897 divide by 9 will always give 3988 + 5/9 no matter how you express the individual components.




Mathematics

Adaptive (sort of) comments tag- code

Continued from here.

I can't get the HTML code to be displayed. The instructions saved as a *.txt file available here.

[Yvy has highlighted a problem: the code cannot be shown by certain browsers because IE will automatically read the stuff and execute the instructions given in the code. Firefix users should be fine. Solution: switch over to Firefox lar...what are you guys waiting for? For your 4 grilled chicken wings? Anyway, IE users, "Save target as..." and save codingexercise.txt to your hard disc as a txt file. Make sure you change it from HTML to txt format. IE is fiddly. I'll see if i can get browsers to display the code. Maybe tonight... Also, come to the dark Firefox side.]

The variable a represents the number of comments. The various if conditions are such that if (condition) is true, {do something}. If (condition) is not true, proceed to next (condition). The last one is a simple else {do this}.

I have not tried these, but it might be possible to design more complicated conditions, such as:

if (a%2==0)
-> If a divided 2 has remainder zero (implies that a is an even number)

if (a!=5)
-> If a is not equal to 5

if (a==3 || a==7)
-> If a is 3 or 7
-> With ||, at least one of the conditions must be satisfied

if (a>=10 && a<20)> if a is greater than or equal to 10 AND smaller than 20 (for a = 10, 11, 12... 19)
-> with &&, both conditions must be satisfied

For more information.

Adaptive (sort of) comment tags

I've modified the java code (presumably its java...) to adapt to the number of comments, n.

n=0 -> No food ordered
n=1 -> 1 bowl of laksa
n=2 -> 2 glasses of teh tarik
n=3 -> 3 cups of coffee
n=4 -> 4 grilled chicken wings
n=5 -> 5 bowls of rice
:
:

The current version is a purely experimental one, and only runs up to ## (I'm not disclosing my limitations. Yet)

The code will be coming shortly.

And no, I am no glutton. It's just that most readers are Malaysians, and most Malaysians have a thing (or two) for food.

The JFE 8555 problem

The Sum of Digits:


On the 28th of July, blogger JFE 8555 highlighted an interesting phenomenon to do with the digits of numbers.

See this for the original version by the author himself itself.

Below is an example done using a 5-digit number, 35997.

We will attempt to add the digits together in any arbitrary manner, repeating till we reach one digit.

35897
-> 3 + 5 + 8 + 9 + 7 = 32
-> 3 + 2 = 5

(35) + (897) = 932
-> 9 + 3 + 2 = 14
-> 1 + 4 = 5

(3+5) + (8 + 9) + 7 = (8) + (17) + 7
-> 8 + (1+7) + 7 = 8 + 8 + 7
-> 8 + 8 + 7 = 23
-> 2 + 3 = 5

3 + 58 + 97 = 158
-> 15 + 8 = 23
-> 2 + 3 = 5

The flabbergasted reader might want to try a few other combinations for amazement’s sake.

Tomorrow, the explanation!




Mathematics

The spirit summoner needs help

One of my engineering subjects involves a sub-subject called “Professional Practice”. Part of it entails participation in debates.

Unlike certain parliaments, the debates do not involve any fist fights nor chair throwing stunts. Neither have I heard of participants shedding tears during a session.

***
The night was silent. Silent, by his definition, was an absence of people sounds. The complex was silent- no intrusive footsteps along galvanised steel walkways, no chatting plant engineers, no annoying nasal sniffles.

The whining of electric motors, rumbling of drive belts, periodic chattering of worn bearings, continuous whoosh of exhaust fans, and interminable roar of turbulence in pipes did nothing to detract from the silence of the night.

The fact that the area is continuously lit by the harsh glow energy saving tubes regardless of day or night, and the fact that it has never seen natural light for 25 years anyway, did not detract from the nightliness of the moment.

It was a silent night. He treaded mindfully, careful not to break the silence with the sounds of his contaminating footsteps. Arriving at a secluded area between two grinding mills, he prepared the scene. It was time to summon the spirits.

From his breast pocket, he extracted a pair of pink coloured candles. Standing them on the floor, he lit one of them. The each of the candles represented one of the Holy Cardinal Numbers of Deterministic Computing: One and Zero. The lit candle, with its flickering flame of carbon yellow, was One. The unlit candle and its pristine wick was the incarnation of Zero.

His fetishes set up, he then proceeded to boot up his notebook computer and connected to the plant’s wireless network. With that done, he chanted the following verses, his rich tenor voice overlaid by the grinding mill’s granulated song.

“By the power vested in me by the ADSL connection, I summon the sentient spirits of the blogosphere to come to my aid.”

He always felt a tinge of stupidity at that ADSL bit, in an era where asymmetric digital subscriber lines are mere playthings of juveniles and college students. This was the age of the fibre optic connection. Still, traditions remain, and ADSL is the phrase to use.

“Spirits of the blogosphere, come forth. Come forth, I implore you, to improve the overall lead time of my task. With your noble aid, the efficiency of completing this task would be improved dramatically. Spirits of the blogosphere, come forth!”

At the end of the proceedings, he was standing between the binary candles, hands high up in the air, reaching for the spirits.

***
Sorry I got a bit distracted. Anyone can help add to the following half-list of arguments? Thanks.

[A small country] should just make a few things well and import the rest.

For:
The local industry will have lots of people experienced in the relevant areas
Improve efficiency- all parties involved are well versed in the tasks involved
Reduce cost- juicier profit margin for the workers and local economy

Against:
Not all citizens share the passion for work in the specialised fields
Overly dependent on external factors
Local industry inexperienced in other areas

Narration

Why is there an orange in my coffee press?

In the parlance of televised motorsports, this blog entry would probably be called a 'splash and dash'. In other words, a quickie. I'm stressing over some stuffy HR Mgmt essay due in 9 hours, with lots to work out.

Yesterday night, a digital camera was floating about in the aether of my apartment. I decided to unwind (from HR research) by taking some still life images. Owner (Mr. BZY) needed it for his academic work, so I had to stop playing after 10 minutes.




Orange Crush
Why is there an orange in my coffee press?




6.43am
I've finally finished that ass of an essay and submitted it electronically. Good thing I have Mondays off, else I'll be turning up in lectures in a fuzzy state of consciousness.



Photography

Taekwondo videos

[patience: 2 video files at 2.9Mb each]

I borrowed a digital camera and used it to aid my pattern training for the upcoming martial arts competition. Having an instant replay of sorts is extremely useful for pointing out potential trouble spots- an inaccurate stance, an impotent block, a clumsy kick, ad infinitum.

You might have been unfortunate enough to hear me going on about the new pattern I picked up some weeks ago from a book. This is it, Jitae, the 6th-dan WTF pattern. Simple, concise, but very technical and with an apparent emphasis on the stances.


Duration: 1:13

I’m still quite hesitant at many parts.

This is a more familiar one, Taebaek, the 3rd-dan WTF pattern. I almost know this like the back of my hand (pardon the pun). More fancy details found in this compared to the Jitae, but one can sometimes fudge the stances without really looking stupid.


Duration: 1:10

Like a writer too familiar with his own paragraphs and blind to his own errors, I would greatly appreciate it if someone helps proofread the patterns.


Personal

Here's a puzzle

Here’s a really horrible puzzle to keep you on the edge of your seats. If/when you know the solution, don't spoil it for others. Thanks.

Three men share a hotel room, each paying his fair share of $10 for the room rate of $30.

Later in the night, management calls the reception to say that the room rates have been reduced from $30 to $25. A bellhop is sent to refund the $5 difference to the men.

Deciding that $5 would be difficult to split among three men, the dishonest bellhop decides to keep $2 for himself, and return $3 to the occupants.

Having been returned $1, each of the three men actually paid $9 for their lodging. Collectively, they have paid $27. The bellhop only took $2. What happened to the other $1?

The solution will not be published here. After Sunday 1.00am (+10 GMT), you can request for a solution to be sent via email.

Have fun, and hopefully you will get sleepless nights pondering the missing $1.



Mathematics

The thermodynamics of waste

On the irreversibility and entropy generation of mixing and wastage


We would start by considering waste material. Waste is typically ‘unusable or unwanted material’ (Oxford). Unusable in that any potential good it might have is already practically exhausted; unwanted when a it is no longer deemed beneficial, although possibly still of some benefit.

An example of waste would be an empty ice-cream tub. While it still contained ice-cream, it was useful because it protected the ice-cream from external elements. When the ice-cream is eaten, the container can still serve its function of separating the inside from the outside. However, the end user does not need another container, and the ice-cream manufacturer would rather commission someone to make new tubs than to retrieve empty ones.

Consider the typical route the unwanted ice-cream tub would take on its way to the landfill. It would first be dumped into a household rubbish bin, where a previously clean ice-cream tub would come into contact with other waste materials such as fruit peel, vegetable roots, decaying leftovers and sanitary pads.

Very loosely, one could say that the entropy of the ice-cream tub has increased. To return it to its original, clean, condition, one would need to give it a vigorous scrub to remove unpleasant substances such as fermenting banana skins and menstrual discharge. The very act of mixing the materials together in a common bin has irreversibly created a dirty tub. Yes, you can clean the tub, but it will cost you some work. Thus the irreversibility.

The reader familiar with entropy as approached by Boltzmann might want to consider the number of possible microstates for each of the following case: tub and other domestic refuse separated; tub and other domestic refuse mixed.

At some point in the waste disposal process, the rubbish would be crushed and compressed. What was previously an intact but dirty tub would be deformed and possibly ruptured. This is yet another irreversibility in the process- after stomping on the tub, you could possibly restore it to the pre-stomped state, but at the expense of a lot of restoration work. Again, one could say that the entropy of the tub has increased.


So, what are the implications of increasing the entropy of a certain system? Well, the most important point is that it has become less useful. To demonstrate the point, we will have to clean ourselves of the rank of rotting rubbish, and subject ourselves to the culinary delights of a kitchen.


Suppose we have a kilogram of green beans, and a kilogram of red beans. At the moment, the two kinds of beans are separated in individual bowls. The chef can make red bean soup, green bean soup or a two-bean soup.

The grid below is a very simplified representation of beans in two bowls. Each cell represents a bean, and its colour represents if it’s a green or red bean. At the moment, the reds are clustered with the reds, and the greens with the greens.



Then suppose an idiot comes along and pours the two different beans together into a big bowl, thoroughly mixing them. Upon seeing this mess, the chef would curse passionately in various languages.



While the chef did lose any beans, he did gain a great deal of entropy. He still can make a two-bean soup, but to make either the red bean or green bean soup would requite some additional effort to remove entropy from the mixed beans. That is, it would mean sorting the beans into reds and greens. Thus, we see the usefulness of the mixed beans has diminished greatly compared to the separated case.


Returning to Boltzmann’s definition of entropy, “entropy is a measure of the number of possible microscopic states (or microstates) of a system, consistent with its macroscopic properties (or macrostate)”. (Wikipedia) What this implies is for our bean mixing exercise is that you can rearrange the individual beans while not changing the overall picture.

For example, consider the unmixed beans. You can take 2 red beans and swap their positions. You have changed the microstate of the system, but on the large scale, nothing has changed- the red beans are still separate from the green beans. Referring to the grid model above, you can swap the positions of any pair of red beans and the system would not change. Our model is a 16 by 16 ‘bowl’ with 256 beans. You can reposition the 256 red beans in 256! = 8.5 x 10^506 unique arrangements, and the system remains the same- red beans in one bowl, green beans in the other. Similarly, you can rearrange the 256 green beans in 256! = 8.5 x 10^506 unique arrangements and the system would stay the same. Collectively, you can rearrange the red and green beans in 256! x 256! = 7.4 x 10^1013 ways and the different beans still remain separate.

What happens when the 2 separate bowls of beans are mixed into a large heap of 512 beans? This time, there is no such thing that the reds have to stay in their half of the system and the greens stay in their own half. Like a diverse nation, they are free to intermingle. Now, you can pick any bean irrespective of colour, and swap their positions without changing the system’s macrostate- the red and green beans remain mixed. How many possible microstates are there in this mixed system? We can reposition 512 beans in 512! = 3.5 x 10^1166 unique positions.

This might not look light much compared to the initial unmixed system, but do bear in mind that the exponent 10^116 implies 1166 trailing zeroes in the figure. The number of possible microstates in the mixed system is larger than the unmixed system by 103 digits.

And we are only talking of 512 beans, not really enough to quell anyone’s hunger.


On a final note, the generation of the mixed grid posed an interesting problem. It was done on Excel’s grids, and I did not really fancy having to click on 256 random boxes and replace their colours. The approach taken was to dot a small region with a random pattern. A wide rectangular section was copied from the region and pasted all over the ‘bowl’ in an arbitrary fashion, with some overlap. Then, a tall rectangular section was copied and pasted randomly over the bowl. The approach took advantage of the fact that random structures are in fact more uniform than orderly structures. If you look at a mixed bowl of beans, they would look the same from all directions. If the beans were separated by some partition, from some directions the green would be on the left; from the other direction, red would be on the left.


References:
Concise Oxford English Dictionary, Tenth Edition
Entropy, Wikipedia
http://en.wikipedia.org/wiki/Entropy


Cite this article as:
Tan Yee Wei(2005), "Thermodynamics of waste", from "Snippets of This and That"
http://vapour-trail.blogspot.com/2005/08/thermodynamics-of-waste.html


Mathematics

Yet another silly orange story

As implied in the previous entry, I have a bundle of small mandarin oranges at home. After dinner, Adrian and I took a few and started eating them in our own ways. Adrian peeled them the normal way with his fingers while I used a knife.

At one point, I held the knife in my fist and made some cutting gestures, as (badly) illustrated below.



“It would be interesting if I toss one of these oranges into the air and while they are falling I can cut them in two.”
At that moment I fleetingly recalled horror stories of the Japanese occupation of Malaya during the Second World War whereby soldiers throw babies into the air and bayonet them on their way down.

“Yea, come come come lets do it,” Adrian said. “I’ll throw it to you and you cut it.”

I rummaged in the box and found one that was going soft and on its way to decay. “This would do.”

“I’ll just throw once first and then you can see where it will go.”
“Ok.”
The first throw was too low.
“Higher.”

The next one was perfect, with lots of air time and nearly overhead. No need for further testing, I figured.

Take a half step forward, and raise the blade upwards and forward. The blade, advancing up and forward in a slanted fashion, caught the falling fruit.

At first, the knife was approaching the falling mandarin.
Then, the falling orange and the knife were already past each other, the fruit cut cleanly in two halves.



Back to work.

The orange eater

It was not a very good day.

In the evening, I packed my stuff to go for karate training. Upon entering the changing room, I discovered that I forgot my attire. “Fark CB!” I said in full.

It is impossible to do anything realistic with my jeans, so I gave up and headed home.

To add to my problems, today is also Bad Nose Day, whereby my nose continuously generates a trickle of dilute mucus. It’s so watery that it dribbles out of the nostrils, thus I have to be continuously sniffling and wiping.
[explosion]
And sneezing.

All this sniffling and blowing over the course of the day has given rise to a minor headache, sinus cavities overflowing with watery discharge and fuzzy vision. It is extremely annoying, to say the least.


Early in the night, I gathered a few small mandarin oranges. They are similar to the (expensive) kind we get during CNY that go by fancy names such as wong dai kat (emperor citrus/lime). I then took a knife, and polished its cutting edge for several seconds using a smooth silicon carbide brick. With a sharp knife and several mandarins, I sat at my study desk and started removing the peel.

I leaned back in my tilting chair, feet propped up on the desk, sharp blade in one hand, helpless fruit in the other. I made an equatorial incision around the mandarin, then 8 longitudinal cuts across the equator from stem to ‘butt’. That done, I pried the skin loose with the blade’s tip, starting at the equator and working them loose towards the ends.

Finally, the skin came loose of the flesh in two circular sheets. They look a bit like orange coloured, many-petalled daisies. The fruit was free!

I then ate the fleshy segments. Juicy…


For some bizarre reason, I found peeling mandarins just as, if not more, therapeutic than eating the delicious fruit itself. I suppose it’s the satisfaction of cutting just enough to penetrate the skin, but not enough to damage the flesh. It might be the pleasure of seeing rejected peel generated in elegant, geometric designs. It could be the joy of wielding an obedient blade, sharp but cooperative.


ps. Chi bai headache...

A general guideline to executing strikes and blocks with power without damage to skeletal joints

Allow me to boast a little.

I’ve learned the Taekwando 6th-dan pattern in its entirety. Just as a reference, 5th-dan black belt holders are referred to as ‘Master’. No, I’m nowhere near number six; I’m still loitering at the first rung after 4 years.

[Truncated: uninteresting bit about how I enjoy pattern routines]


A general guideline to executing strikes and blocks with power without damage to skeletal joints. Also a general guide to producing strikes that generate an impressive ‘foop’ sound as seen in fung fu films.

Many beginning practitioners face a problem when attempting to exert force when punching air. Say one is attempting to execute a demonstration punch. If great force is used to drive the fist outwards, it will naturally by moving at high speeds.

At the end of the arm’s reach, the fist will be suddenly stopped by constraints in the skeletal joints. One major shock load occurs in the elbows- when a fist is hurled outwards, the elbow joint unfolds rapidly while rising upwards. At the limit of extension, the elbow can no longer unfold further- it’s straightened to it’s maximum and will bend no more. Unfortunately, the upper and fore arms are still moving rapidly with a general upward direction. The elbow’s constraint causes a severe shock load that stops all motion.

This repeated shock load will be painfully felt if one performs repeated punching drills without sufficient care.

The way to circumvent this impact stopping is to use your muscles to retard the movements just before the punch comes to the limit of extension. Try a very quick strike, where upon impact you withdraw the fist from the impact surface. Notice the muscles drawing the limb backwards. We are interested in using this set of muscles.

Instead of drawing the fist backward as in the previous case, we now want to stop the fist just a slight bit before the impact site. The same muscles will need to tense up abruptly at the stopping point.

The magnificent ‘foop’ sound that appears to convey an impression of forceful execution is generated when stopping the fist. Of course, a proper uniform of sufficiently thick material is necessary. To generate the noise, one would need to execute a very fast strike, and decelerate it very abruptly using the aforementioned muscles. Attempting to use the skeletal joint constraints to do the same will only result in serious injury.

A failing cable; a collapsing relationship

As Euclid walked along the ancient roadway, he noted that forests on both sides of the road were already reclaiming the strip of land. Roots continually growing below the paved surface formed bulges and cracks, and what used to be a continuous surface of black bonded gravel had been reduced to grainy light grey coloured tectonic plates. Grass sprouted up in cracks between individual slabs of tarmac, demarcating the roadway with streaks of green. Where several cracks meet to form a larger gap, under-nourished saplings struggle to grow.

The ancient road came to a wide, lazy looking river spanned by an equally ancient cable-stayed bridge. The bridge’s concrete towers were heavily weathered by carbon dioxide in rain water, and bore ugly smear marks as evidence of the acid rain. Many of the supporting cables had their protective coatings worn away, and some of the cables themselves had worn through. At places where many cables were no longer load bearing, the bridge’s deck sagged visibly. Ages ago, these cables were woven from thousands of fine steel wires, braided into cables that were strong yet slightly flexible.

As he approached a supporting cable near the middle of the bridge’s span, he saw that a portion of the steel wires making up the cable had failed, unravelling parts of the braided cable into a frizzly mess. The remaining fibres that were intact supported a great proportion of the bridge’s load, putting the surviving fibres under high tension.

Looking at the failing cable, Euclid thought of his two friends who were together at the moment. While they were very nice and likable people, these two just did not go very well together. To Euclid’s eye, their relationship was fraying like the braided steel cable. A broken strand would cause the strands to take a greater load, and might aggravate the failure of further strands, thus accelerating the demise of other strands. One day, the tensile loads would exceed the fibres’ limits, and they would snap with exponentially increasing frequency until the entire cable disconnected.

He sighed. Nothing he could do but watch the unravelling situation, both for the failing relationship and the fraying cable.

As he watched the cable, a fibre snapped. Suddenly unloaded from the tremendous tension, both broken ends contracted away from each other with a sharp metallic ping, whipping backwards as the fibre unravelled itself from the main cable. The flying strand contracted into the existing mass of curly wires, causing the loose agglomeration to quiver in a stiff, springy fashion. Anyone whose finger got hit by that wire flying at the speed of sound would no longer be owner and master of that finger.

He sighed again. It’s really coming apart. He could only hope that the inevitable collapse does not injure anyone.



[Do not try too hard to find out who I am referring to. If you try hard enough, you might just find traces of yourself, just like finding your house number from a thousand numbers]

The anatomy of an eye

Yesterday, I had 2 lessons- Optimisation and HR Management. There was a short break between the classes, so I replied a few emails, and explored the biomedical library for interesting books. I found “Prime Mover- a natural history of muscle” by Steven Vogel. The first chapter looks promising enough.

I then went into my lecture theatre, only to see a guest lecturer introducing himself. He then started to discuss the anatomy of the human eye. Shit… this does not look like Human Resources Management. Ruffling through my feathers papers, I found my timetable and realised I was an hour early. So I sat and listened about the human eye.

No wonder the eye is used as an argument for proof of a supreme being’s existence!

Stepping back from theology, here are some key points (minus the correct jargon) that I remember (not with 100% accuracy):

Tears consist of 3 secretions- an oily component, mucus, and the watery bit. Eyelids do not slam shut straight downwards. Instead, the edges furthest from the nose shuts first, and the upper lid sort of comes down like a guillotine. As such, a wiping action is developed upon blinking, pushing the tear film towards the middle of the face. At the ‘inner’ tip of the eye is a little hole which drains the tears into the nasal cavity. Ladies (and some gentlemen) who use eye-liner are advised not to colour that little hole.

The optical nerve carrying visual information out of each eye consists of two channels, one for the left half of the field of vision. Optical nerves from both eyes meet somewhere before arriving at the two half-brains, and they cross over. As such, the right brain received signals from both eyes, but only information about the left half from each eye. Similarly, the left brain receives signals from both eyes, but only information from the right half of each eye.

If you cut a nerve between the eye and the crossing point, the entire eye becomes blind since the information cannot be sent out.

If you cut the crossing point, to sever the crossing nerves, you would blind the patient’s victim’s periphery vision. The right eye can only see left, and the left eye can only see right.

If you cut a nerve after the crossing, the patient cannot see to one side. For example, cutting the nerves leading into the right half brain would cause the victim to be blind to objects on the left side.

I’ll be there next week.

Minum?

If you drop by to visit me in Melbourne, I’ll probably invite you to take a seat. Once comfortably seated, I might inquire with a condescending jerk of my head, “minum?”

“What do you have?”
“The usual.”
“Which is?”

To which I’d abruptly turn around and saunter towards my drinks storage cabinet. I fling open the doors, declaring “7 kinds of tea infusions, 8 bottles of coffee, honey, cocoa, and instant herbal tea.”


OMGWTFLOL
Click for larger image

Actually, a few of the boxes of tea are very nearly empty. Also, several of the coffee bottles are very nearly empty. I’m not entirely to blame.

[12 August 2005 addition]
The count has since increased to “7 kinds of tea infusions, 10 bottles of coffee, honey, cocoa, and instant herbal tea.” Adrian was running out of his usual coffee, thus he purchased a bottle of Nescafe Kenjara. I was also scraping the bottom of my espresso barrel bottle, so I got another espresso. It's an orgy!

Portrait of a sulking girl

[From a sight I saw on 10/7/05, on the ferry from Kangaroo Island, South Australia, back to the mainland.]

After parking our rented car in the ferry’s vehicle hold, I meandered through various corridors, bulkheads and stairways to arrive at the main passenger deck.

A small counter operated at the rear end of the passenger lounge selling candy, coffee, pastries and drinks. Around it, a loose clump of passengers lingered- some waiting for their lattes, others contemplating the pastries on display in their display case, yet others simply tagging along with someone else. A coffee machine hummed as it percolated shots of espresso, and hissed as its steam jet helped froth a mug of milk. The cash register’s drawer rolled back and forth with rumbles and clicks as transactions progressed. Cappuccinos, pies, sausage rolls, beers, lollipops and juices went over the counter; cash came in return. Wallets folded and purses zipped, coins clinked, notes rustled.

I found my friends seated at the front row of the passenger lounge, facing several large windows that looked out onto the fore deck and the sea.

At a window nearby, a young girl of about 7 sat on the window sill with her back leaning against the reassuringly thick glass pane. She appeared to be brooding with a slight hint of annoyance, sulking slightly at some minor irritation. Her father leaned forward from his seat to speak to her. She turned to look at him, listening with a distant expression, and gentle shook her head once. He made another attempt to convince her to sit on the seats, and she rejected him with the same serenely concise shake of her head. After a while, the father decided to let her annoyance mellow out, and he turned to tend to his other children.

The girl continued sitting on the window sill, hands resolutely crossed over her chest, observing passenger activity in the lounge. She appeared to be reluctant to look at her father, but instead stared alternately at the fuzzy TV images, the coffee counter and out into the cloudy morning sky.

Passengers continued boarding the ferry. As they entered the passenger lounge, they would slow down with their eyes looking this way and that as they evaluate the desirability of various available seats. Is it near the window? The man next to that seat doesn’t look pleasant. I do not want to be near to the toilets. I prefer a forward facing seat to a backward facing one. There’s a pretty girl! I don’t want to sit unnecessarily close to strangers.

At that moment, the dull and water sodden clouds stirred, parting to reveal the morning sun. The sun’s rays painted the cabin with elongated strokes of rich yellow shafts that came through numerous windows, suffusing the entire cabin in a light golden tincture. The mood in the cabin appeared to lighten considerably.

Sunlight entered the girl’s window obliquely, illuminating her wavy blonde-brunette tresses from the side, highlighting some, shadowing others. Something caught her eye, and she turned her head slightly towards it. Golden rays from the sun shone on her eyes at an acute angle, too slanted to enter her pupils. Nonetheless, the light did hit her irises, illuminating their brown colouration with a brilliant wash of gold. In the sunlight, her brown eyes shone with a colour of light wood gently coated with diluted caramel.

She continued looking, her face set in that same expression of calm mild annoyance, hands still crossed over her chest, the sun highlighting her hair, and eyes shining with a golden brown light. Beside her on the window sill, a toy stuffed horse lay in a limp heap, not entirely forsaken but temporarily ignored.


* * *

It would have been a dramatic portrait if one could capture the image without disrupting the lass’s facial expressions. Of course, that would be extremely difficult. So I had to be content with taking occasional glances at the extremely rare scene in front of me. Staring would not do- it could possibly freak the girl out and she would… who knows what she might do. For all we know, she might hop down from the window sill, goosestep march towards me and give my shin a good hard kick with her steel-toed sandals, transferring all her momentum through the steel-toe.

About 15 minutes into ferry ride, the girl softened up and moved from the window sill to the proper seats next to her father, which happened to be next to my seat.

I turned to her, and greeted her with a cursory “hi”. When the surprise melted from her face, she smiled brightly and waved in return.

Kitchen accident results in loss of blood.

Recently I cut myself with the one of the sharp knives I have in the kitchen. Disturbingly, it’s the second time in about 5 weeks. I haven’t been cut by a knife in many years, and getting slit twice is plain humiliating.

The first accident happened a few days after I boasted about my knife sharpening skills. While making myself dinner, the knife somehow fell off the counter. I was not so stupid as to try catching the falling knife; as had become instinct, I quickly realigned by feet to snap them away from danger. Unfortunately, my thumb was near the falling scene, and the knife’s cutting edge happened to strike my thumb.

The cut itself was not painful, but it was very deep. Sharp blade ma. The bleeding continued long after I applied a bandage to the laceration, soaking the plaster with a messy red fluid.

Yesterday, I was slicing mushrooms. All was going fine- the knife had adopted a sure rhythm, and mushroom slices were being generated at a steady pace. A slight mismatch in relative velocity resulted in the knife moving before the fingers had relocated properly, causing the blade to come onto the left index finger.

If I did not have fingernails, it is conceivable that the blade would cut through soft tissue and tendons all the way to the bone. If I did not have bones in my finger, the last 15mm of finger would probably have dropped off.

Getting cut is embarrassing. Having played with for knives almost daily for two years already, this should not have happened. I ought take better care, and lose some of that overconfidence.

Happy Birthday to Mom

Today (9 August) is my mother's birthday. I don't think she'll read this, but nonetheless,

Happy Birthday Ma!

Love,
Wei.

[mathematics] From another point of view...

Assumed knowledge: minimal
Difficulty: 2/5
Tedium: 1/5
Insight: 3/5


Content adapted from “The Beauty and Zen of Mathematics” seminar by the Melbourne University Mathematics and Statistics Society (MUMS).

The problem presented below is used to highlight an elegant approach to solving a particularly nasty mathematical problem.

a + b + c =100; a, b & c are natural numbers (integers greater than zero)
How many possible solutions are there?

To answer the question, we can try counting the number of solutions.
Fix a = 1:
1 + 1 + 98 = 100
1 + 2 + 97 = 100
1 + 3 + 96 = 100
:
:
1 + 98 + 1 = 100

For a = 1, there are 98 possible solutions. What about for a = 2?

Fix a = 2:
2 + 1 + 97 = 100
2 + 2 + 96 = 100
2 + 3 + 95 = 100
:
:
2 + 97 + 1 = 100

For a = 2, there are 97 possible solutions. What about for a = 3, 4, 5, 6 ... 98?


Without crunching numbers for all possible values of a, the semi-enlightened soul might notice that the number of solutions is
98 + 97 + 96 + … + 2 + 1 = 4851.
There are 4851 solutions.


There is an easier approach.
Consider 100 dots arranged in a line:
o o o o o o o o o o o o … o o

-The ellipse shows that the series has been truncated to save on space

1 + 1 + 98 = 100 (a = 1; b = 1; c = 98) can be represented by grouping the dots into groups of 1, 1 and 98, where the first group is for a, the second for b, and the third for c. The grouping will be done by partitioning the dots:
o | o | o o o o o o o o o o … o o

Similarly, 5 + 2 + 93 = 100 (a = 5; b = 2; c = 93) can be represented by grouping the dots into groups of 5, 1 and 94 as shown:
o o o o o | o o | o o o o o … o o

The problem is now reduced to counting how many ways the 2 partitions can be inserted into the 99 gaps between our hundred dots.
The answer is simply 99 C 2 (read “99 choose 2”) = 4851



Finally, some weird word games from the MUMS magazine:


and

The volume of a circular pizza of thickness a and radius z is simply pizza.

It's sleep paralysis, not a ghost

[started writing on Thuesday]

For the past 10 to 15 years, I have scoffed at afternoon naps just like I ignore the horoscopes, fortune telling or chain mail. Napping was (and still is) deemed a waste of good consciousness.

Over the last year, I finally saw the power of the nap. In the absence of lectures and parental nagging, my sleeping time tends to migrate toward an equilibrium position of 6am to 1.30pm. However, when a 9.30am exam pops out of the quantum foam into existence, the sleep times have to be modified drastically to allow this deformed piece into the jigsaw puzzle. Naps of varying durations could be inserted into the ‘day’ to lengthen the waking hours, thus helping make 9am to 12pm a non-sleeping period. That is the power of the nap.

I took a nap this afternoon due to a prolonged lack of sleep, but it was not very fruitful. My brain kept snapping into consciousness and would erupt into an irrelevant hive of activity before abruptly winking back into nothingness. Not the slightest bit conductive to restful sleep.

I woke up to yet another spurt of mental activity.

I could not move.

I tried to twitch my hands but they seemed to be restrained by some force.

I imagined that some sort of phantom hand was pinning me down. A panic starts to come.

I strained to move my hands again, this time instinctively trying to exhale at the same time as shoving.

I noticed my mouth was firmly in ‘half-open’ position. I could not get it to go to ‘close’. It felt as if the jaw had been rigidly bonded to the skull.

The panic had multiplied many-fold; it was overwhelmingly distressing.

The imaginary loads suddenly disappear, and I could move.

I found that I was still disoriented from the experience.

All of the above lasted less than 2 seconds. Despite the short duration, it was a frightful experience. It is very likely that one would immediately point the source of the phenomena at a kuai or succubus. However, a few minutes of post-trauma pondering convinced me that it was not the result of paranormal activity.

My hand did not feel any force clamping it down.

My muscles did not tense.

Hence my hand was not moving to my command not because something was resisting my muscles’ contractions, but because there were no muscle contractions in the first place.

The same argument can be applied to the jaw.

In general, it appears that the skeletal muscles were not responding.

These appear to be in agreement to something I have read in the past about sleep paralysis.




The below is a cursory introduction to sleep paralysis:

Sleep paralysis consists of a period of inability to perform voluntary movements either at sleep onset or upon awakening.

Symptoms of sleep paralysis:
A complaint of inability to move the trunk or limbs at sleep onset or upon awakening
Presence of brief episodes of partial or complete skeletal muscle paralysis
Episodes can be associated with hypnagogic hallucinations or dream-like mentation (act or use of the brain)

There is no known explanation why some people experience this paralysis. It is not harmful, although most people report feeling very afraid because they do not know what is happening, and within minutes they gradually or abruptly are able to move again; the episode is often terminated by a sound or a touch on the body.

In some cases, when hypnogogic hallucinations are present, people feel that someone is in the room with them, some experience the feeling that someone or something is sitting on their chest and they feel impending death and suffocation. That has been called the “Hag Phenomena” and has been happening to people over the centuries. These things cause people much anxiety and terror, but there is no physical harm.

-Sleep Well

The condition is characterized by being unable to move or speak. It is often associated with a feeling that there is some sort of presence, a feeling which often arouses fear but is also accompanied by an inability to cry out. The paralysis may last only a few seconds. The description of the symptoms of sleep paralysis is similar to the description many alien abductees give in recounting their abduction experiences. Sleep paralysis is thought by some to account for not only many alien abduction delusions, but also other delusions involving paranormal or supernatural experiences (e.g., incubus and succubus).

-Skeptic's Dictionary

Macro photography of green stuff

Set up:
Borrow digital camera.
Sharpen knives.
Brew a good cup of coffee.
Slice fruit.
Cut 1/8 of a mooncake.
Clean and polish window pane using detergent, sponge, cloth and old newspaper.


The fruit used was kiwi fruit. I like kiwi for its translucence, details in the seed arrangements, slightly textured flesh and the unmistakable vibrant green. I planned to cut a thin slice (1.5 to 2.0mm) and slap it on the very clear window pane, and let sunlight illuminate the slice while I get the skyline in the background. It turned out to be a bad idea- my apartment’s balcony is made of ugly galvanised steel sections and did not do the composition any good.


Click to enlarge

It was a fine day, with minimal cloud cover and very clear air. The sunlight was very bright and direct. It’s my first attempt at taking photos with such strong light, and I’m actually quite happy with the results.


Click to enlarge

The mooncake in question is one of a Golden Pandan flavour. It sounds very weird compared to more pedestrian variants like red bean or lotus seed paste.


Click to enlarge

Look, its bloody green! The degree of greenness did give me a surprise. Upon eating, it tastes similar to a kaya puff with the pandan filling and the surrounding pastry material.


Click to enlarge

The very smooth cut surface of the mooncake was achieved with a sawing motion using a very sharp blade. Without the sawing motion, and only exerting pure compression, the paste will part away with a grainy texture at the surface instead of the smooth sheen seen here, and the pastry would crumble unevenly.

This was my work surface early in the activity with a mug of coffee to keep me happy and tissue paper to pat dry the fruit slices- wet, juicy slices do not reveal their details easily. By the end of the shooting session, the entire fruit was decimated into thin slices drying in the sun and little bundles of kiwi juice moistened tissue paper were strewn over the table.


Click to enlarge

The galvanised steel balcony railings are visible outside the glass doors, and the ugly square section steel column for the balcony is just visible at the edge of the window.

The apparent ease of divisibility of numbers using different bases: a graphical approach

Most, if not all of us are familiar with the base-10 notation of numbers, where ten symbols are used to represent numbers. These tem symbols are as follows:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9

With only ten symbols, we need the represent the infinitely many numbers that we can possibly come across. Hence, several symbols are strung together to represent larger numbers. After nine (‘9’), we are already out of symbols, so we add an additional digit (‘1’) and return the first digit to ‘0’. Thus, the number after nine is represented by ‘10’. The last symbol is then incrementally advanced until we run out of symbols, and the next digits advanced by one symbol. When the second digit reaches the last symbol ‘9’, a third digit is added, and thus the number after ninety-nine (‘99’) is represented using three digits (‘100’).

The natural numbers expressed in base-10 would look like:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22…

History is such that the base-10 system spread to Europe and persisted. In other early cultures, base-5 (one for each finger), base-12 (one for each finger-bone excluding the thumb) and base-60 (the Babylonians used base 60, and this is why the minutes and seconds are in odd 60s.)

If we used base-12, we would need twelve symbols. We shall use
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b

The same set of natural numbers expressed in base-12 would look like:
1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1a…


Returning to the more commonplace base-10 notation, it is easy to see that 6558 can be divided by 2. It is also trivial to see that 6558 cannot be divided by 5. However, it is not as trivial to tell if the same number can be divided by 3.

Using base-10 notation, we can write the numbers in a grid form, such that the width of the grid is ten columns wide.



To show the ease of divisibility by two, we will collect the numbers into groups of twos. Numbers that can divide by 2 are marked in red. As the diagram below would clearly show, all the red numbers occur in the same columns. The conclusion is that in base-10, all numbers that end with the symbol of ‘0’, ‘2’, ‘4’, ‘6’ or ‘8’ can be divided by two.



The same can be said of division by five, as the next illustration will show. All base-10 numbers ending with ‘0’ or ‘5’ can be divided by five.



However, three is a tricky one. All numbers that divide by three are spread out over the grid. As such, divisibility cannot be confirmed from the last digit alone.



Repeating the same exercise for base-12:
Write the numbers in a grid.



Group numbers together in pairs to check for division by 2.



Group numbers together in pairs to check for division by 3.



Group numbers together in pairs to check for division by 5.



We have seen that divisibility is easy to confirm if the last digit can be used to judge the divisibility. From the above examples, using the last digit as a means of evaluating divisibility is only valid only if the groups of numbers stack exactly on top of one another.

If we write the number in base-n, and wish to divide the number by k, then the stacking occurs if and only if n can be divided by k. For example, 10 can be divided by 2, such that at every new row, the number groupings start from the first number instead of continuing from the previous row (like that seen in base-10, division by 3).

Happy Birthday

Yesterday (Thursday 4/8/05) was a friend TMC’s 21st birthday. Today (Friday 5/8/05) is housemate Adrian’s 20th birthday.

The couple’s mutual friends brought them out for dinner yesterday in celebration of their popping into existence 2 decades (and a year) ago. Most of us used to stay in the same apartment complex- that’s how we knew each other. Most of us having moved out earlier this year, and we rarely get together for dinner anymore. It was nice to meet up again.

We purchased some beer after dinner. In the 7948 days or so since my birth, I don’t think I’ve ever had a beer. Surprising? Don’t really find alcoholic drinks appealing- they are always too ‘dry’ for my liking.

So TMC’s 21st birthday was also the day I had my first ever beer. It was a bottle of Mexican Corona with a sliver of lemon shoved down the bottle opening. Wouldn’t say I liked it, but it was very bearable, unlike most wines and hard liquor.

Actually, the photography was more interesting that the beer. Pity I did not have my tripod with me; had to stabilise the camera against the table top, thus limiting the positions I could shoot from.


Click for large image


Click for large image

They are all in portrait orientation. Landscape will not do- attempting the capture the bottles would entail capturing the person sitting just right of the frame, or the horrible mess on the table just left of the frame.

By the way, I’ve got this thing for taking macro shots through bottles, half filled wine goblets, water surging into a glass, thin slices of fruit and other (semi) transparent medium.

Once again, a happy birthday to TMC and Adrian.

Postcard

It’s particularly advantageous to learn specialised arts from different experts to get a wider view of the entire situation.

While in college in Malaysia, my mechanics lecturer was a Dr Gowda, an Indian national. Gowda writes his vectors in this form: r = xi + yj. The vectors are marked by underlining them with a squiggle ~. For cross products of unit vectors, this little relationship is used:
i, j, k, i...
If the two unit vectors come one after another, then the product is the third vector: i x j = k or k x i = j.
If they go backwards, then the product is negative: j x i = -k.

At Melbourne, the lecturer who handles all dynamics courses is a Dr Krodkiewski of Polish origin. He writes his vectors in this form: r = ix + jy and the vectors underlined with a squiggle. He never needed any tricks to obtain the cross products of unit vectors: everything is done in full, by expressing them as a sum of i j k and doing the cross product via the matrix determinant. While the style is tedious at times, but mechanical and not prone to errors due to brain fade. The same could be said of Krodkiewski’s approach to derivations and calculations- all the procedures are done precisely, step by step, very formal and easy to proofread.

Recently, the university pawned a Prof Pandy from Texas A&M for a position in biomechanics. He does things a bit differently. Instead of ΣF = ma, Pandy uses D’Alembert’s approach of ΣF – ma = 0. An extra vector is added into each object, the inertia force ma. The problem is then solved like in statics. For the cross product of unit vectors, he uses the right handed screw to visualise the problem. I can illustrate hand motions with text, so we’ll not talk about that. He underlines his vectors using a straight line instead of a squiggle.

Enough rubbish for today.


Just for fun, the third person to email his/her full postal address to bare_proton[at] yahoo.co.uk will get a postcard from Melbourne, Australia. Open to everyone, even if I do not know you, wherever you are. Enter "Postcard" in the subject line. [event closed]

Profit margin > 1500%

About a year ago, the student union library was cleared out a less popular chunk of their collection. All books were piled into boxes and marked A$2 each, or $7 for four. After giving them a quick glance, it did not come across as surprising to see that no one loans these books.

An image of a race car caught my eye; race cars always get my attention. The book was an Autocourse book, the definitive Grand Prix annual book. I dug around, and found 3 more of these. Going on their reputation alone, I decided to buy all four of them. $7 is a decent price to pay for a few infrequently loaned, library maintained books.

They were 4 books from the late 80s, the era of Niki Lauda, Alain Prost and Nelson Piquet. It was also the start of the turbo era, where 1.5 litre engines were turbocharged to produce up to 1500 bhp (BMW).

Today, I had a sudden impulse to approximately valuate these 4 books. Ebay was used to give me a rough guide.

These same books are going for US$ 30 each.

At another site, which probably sells stocks of brand new books, these editions sell for US$95 to US$150. Muahaha!

Bad Writing

A friend sent me a link with the remark, “I have a feeling this is something you might write.”
http://news.yahoo.com/[address truncated]/odd_badwriting_dc
Note the bad writing.

LOS ANGELES (Reuters) - A Microsoft analyst has won an annual contest celebrating bad writing by comparing fixing carburettors to fondling a woman's breasts.

"As he stared at her ample bosom, he daydreamed of the dual Stromberg carburettors in his vintage Triumph Spitfire, highly functional yet pleasingly formed, perched prominently on top of the intake manifold, aching for experienced hands, the small knurled caps of the oil dampeners begging to be inspected and adjusted as described in chapter seven of the shop manual," went Dan McKay's winning entry in the Bulwer-Lytton Fiction Contest.

McKay, 43, of North Dakota was said by organizers on Thursday to be visiting China "perhaps to escape notoriety for his dubious literary achievement." He wins $250.

-view full article here

I’m actually quite flattered that someone compared me to this work of art. Realistically, I’m nowhere close (yet).

On another note, I’m having trouble with reading material; there is simply too much of them at the wrong times. During the semester, when I have the odd hour between lectures, I often dig around the libraries, finding more interesting books than I have the time to read. During the winter holidays, I sort of rotted at home whiling away my time with unimportant activities.

Current reading list that does not include stuff from my course:

Global Governance and International Relations essay
Foreign Policy of Developing States essay
From One to Zero- a universal history of numbers
Zero- the biography of a dangerous idea
Accounting (a text book that somehow landed in my lap)
Mass Communication Theory- foundations, ferment, & future

Oh, why am I doing this? Does anyone need to know? No. Can my time be better spent? Yes.