The number of elementary operations to calculate the determinant of a real, k-by-k matrix
The pleasure of (self) discovery is great.
This post is a hedonistic repetition of something I played with on Thursday night. There are no jokes in today’s entry.
Contents:
Introduction- the matrix determinant
Counting the number of elementary operations needed to find the determinant
Expressing the number of elementary operations as a non-recursive function
Proof by induction that the two expressions are equivalent
Cite this article
End note
Introduction- the matrix determinant
The determinant of a matrix A can be expressed as the following:

Where Cij is the cofactor of aij, and Mij is the minor of A formed by removing row i and column j.
The number of elementary operations required to calculate the determinant of a k-by-k matrix will be denoted by f(k).
Counting the number of elementary operations needed to find the determinant
As the definition shows, |A| is a sum of k terms. Each term consists of a multiplication of an element with its cofactor. To count the operations required: summing k terms would require (k-1) addition operations; there are k multiplication steps, and there are k different cofactors to determine. Each cofactor is the determinant of a (k-1) by (k-1) matrix. Note that the step (-1)^(i+j) in the cofactor has been neglected because it is a computationally simple operation of sign flipping.
Thus f(k) = (k-1) + k + k*f(k-1)
f(k) = k[2+f(k-1)] -1.
The trivial case for this recursive equation starts at f(1)=0. Knowing this, all other values of f(k) can be determined by recursion.
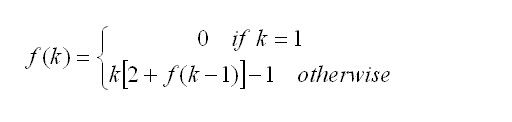
Expressing the number of elementary operations as a non-recursive function
Calculating f(k) algebraically for several cases of k, it appears to take the following non-recursive form:
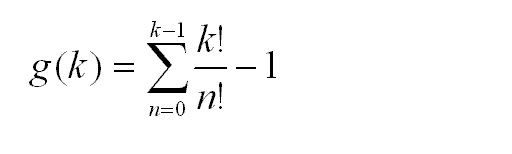
Proof by induction that the two expressions are equivalent
To show that g(k) is an alternative representation of f(k), g(k) = f(k) will be proven by induction. The first case g(1) = f(1) will be proven. Then, assuming that g(k)=f(k) is true, g(k+1) = f(k+1) will be proven. By showing that g(1)=f(1), the second argument can be applied to show that since g(1) = f(1), then g(2) = f(2). Applying the second argument again, it can be shown that since g(2) = f(2), then g(3) = f(3)…
First, show that g(1) = f(1).
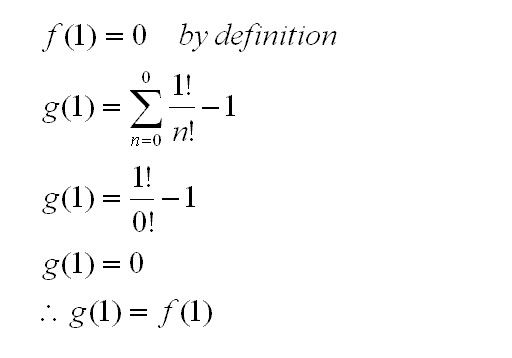
*Note that 0! is defined to be 1.
Now prove that if g(k)=f(k), then g(k+1)=f(k+1).
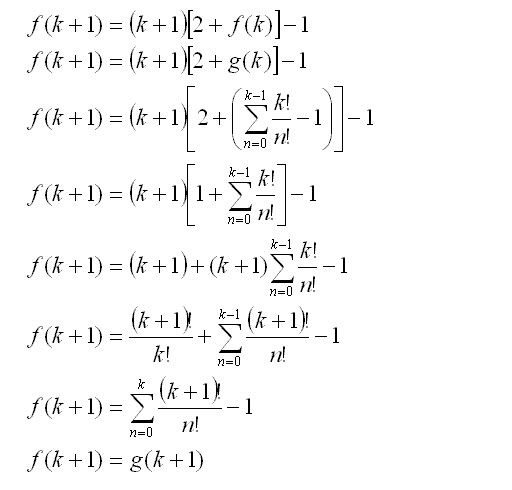
*Pay attention to the factorial signs. They are sometimes not quite visible.
Thus the number of elementary operations required to calculate the determinant of a k-by-k matrix is shown to be
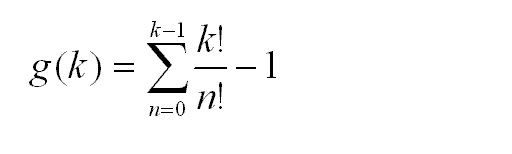
Cite this article
Tan Yee Wei(2005), "The number of elementary operations to calculate the determinant of a real, k-by-k matrix", from "Snippets of This and That"
http://tanyeewei.blogspot.com/2005/10/number-of-elementary-operations-to.html
End note:
A mathematician, a physicist, and an engineer were trying to show that all odd numbers greater than 1 are prime numbers. The mathematician says, “3 is a prime, 5 is a prime, 7 is a prime. By mathematical induction, it follows that all odd numbers greater than 1 are prime.”
The physicist gives his explanation, “3 is a prime, 5 is a prime, 7 is a prime, 9 is an experimental error, 11 is a prime.”
The engineer then says, “3 is a prime, 5 is a prime, 7 is a prime, 9 is a prime, 11 is a prime, 13 is a prime, 15 is a prime.”
Mathematics
This post is a hedonistic repetition of something I played with on Thursday night. There are no jokes in today’s entry.
Contents:
Introduction- the matrix determinant
Counting the number of elementary operations needed to find the determinant
Expressing the number of elementary operations as a non-recursive function
Proof by induction that the two expressions are equivalent
Cite this article
End note
Introduction- the matrix determinant
The determinant of a matrix A can be expressed as the following:

Where Cij is the cofactor of aij, and Mij is the minor of A formed by removing row i and column j.
The number of elementary operations required to calculate the determinant of a k-by-k matrix will be denoted by f(k).
Counting the number of elementary operations needed to find the determinant
As the definition shows, |A| is a sum of k terms. Each term consists of a multiplication of an element with its cofactor. To count the operations required: summing k terms would require (k-1) addition operations; there are k multiplication steps, and there are k different cofactors to determine. Each cofactor is the determinant of a (k-1) by (k-1) matrix. Note that the step (-1)^(i+j) in the cofactor has been neglected because it is a computationally simple operation of sign flipping.
Thus f(k) = (k-1) + k + k*f(k-1)
f(k) = k[2+f(k-1)] -1.
The trivial case for this recursive equation starts at f(1)=0. Knowing this, all other values of f(k) can be determined by recursion.
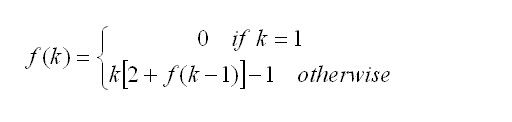
Expressing the number of elementary operations as a non-recursive function
Calculating f(k) algebraically for several cases of k, it appears to take the following non-recursive form:
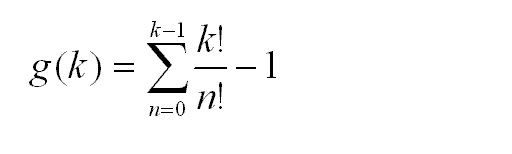
Proof by induction that the two expressions are equivalent
To show that g(k) is an alternative representation of f(k), g(k) = f(k) will be proven by induction. The first case g(1) = f(1) will be proven. Then, assuming that g(k)=f(k) is true, g(k+1) = f(k+1) will be proven. By showing that g(1)=f(1), the second argument can be applied to show that since g(1) = f(1), then g(2) = f(2). Applying the second argument again, it can be shown that since g(2) = f(2), then g(3) = f(3)…
First, show that g(1) = f(1).
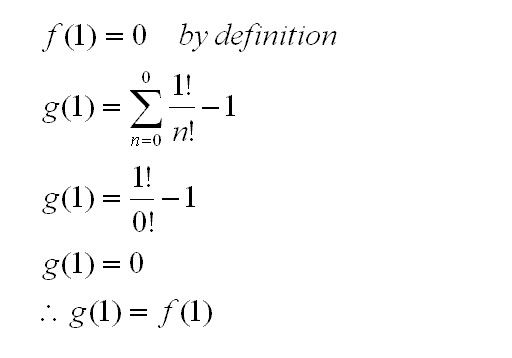
*Note that 0! is defined to be 1.
Now prove that if g(k)=f(k), then g(k+1)=f(k+1).
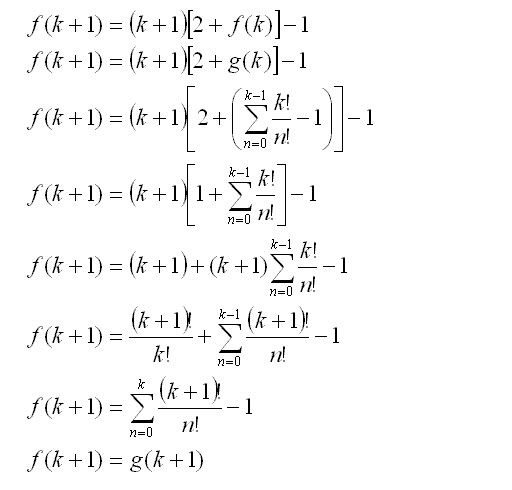
*Pay attention to the factorial signs. They are sometimes not quite visible.
Thus the number of elementary operations required to calculate the determinant of a k-by-k matrix is shown to be
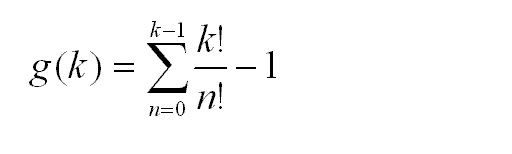
Cite this article
Tan Yee Wei(2005), "The number of elementary operations to calculate the determinant of a real, k-by-k matrix", from "Snippets of This and That"
http://tanyeewei.blogspot.com/2005/10/number-of-elementary-operations-to.html
End note:
A mathematician, a physicist, and an engineer were trying to show that all odd numbers greater than 1 are prime numbers. The mathematician says, “3 is a prime, 5 is a prime, 7 is a prime. By mathematical induction, it follows that all odd numbers greater than 1 are prime.”
The physicist gives his explanation, “3 is a prime, 5 is a prime, 7 is a prime, 9 is an experimental error, 11 is a prime.”
The engineer then says, “3 is a prime, 5 is a prime, 7 is a prime, 9 is a prime, 11 is a prime, 13 is a prime, 15 is a prime.”
Mathematics
Labels: mathematics, number theory

<< Home