Should you replace your car with a newer model with lower fuel consumption?

Contents
1. Introduction
2. Method of analysis
Choice of test cases
Valuation of cases
Cost function
Optimum solution
3. Sample problem
Available options
Cost functions
Solution method
Choosing a non-optimum choice



Introduction

Advancements in automotive power plants have produced cars with ever improving fuel efficiency. In some instances, it may be a better choice to trade in an old fuel guzzler for a newer vehicle. Other times, it may not be a financially sound move. This paper will show how some variables will affect the decision making process.

Method of analysis

Choice of test cases

The available set of test cases is preselected by the user to account for personal preferences. For example, a user may choose to consider buying a Honda Accord, a Nissan Cefiro, or stay with the current vehicle. While there are numerous other choices available in the market, these are may not be included in the test because the user deems these unfit for consideration, based on price and preference.

Valuation of cases

Each case is valued based on purchase price and fuel consumption. Depreciation/resale value is not considered as this is not easy to predict for people unfamiliar with the used-car market. Cost of maintenance and repairs is also not considered as reliable records are difficult to obtain.

Valuation is performed on a cost per month basis, where the costs consist of:
Fuel- dependent on expected driving distance in a month, fuel consumption of the car and cost of fuel
Opportunity cost (lost of potential investment income)- dependent on money invested in obtaining a new car (after accounting for the resale price of the current vehicle) and the expected rate of return in the capital market

Cases are compared on basis of cost, and the case which presents the least cost is the optimum choice.

Cost function

The cost of fuel is the product of distance driven per month, the quantity of fuel used per km, and the price of fuel.

Z = dηp + c[(1+i)1/12 - 1]

Where:
Z is the total cost per month
d is the expected distance driven in a month
η is the fuel consumption per km
p is the price of fuel
c is the cost of obtaining a new car
i is the rate of return in the capital market

The term c[(1+i)^1/12 - 1] indicates the returns from investing in the capital market that would be had if the money had been invested rather than being spent on the new car.

Optimum solution

The optimum solution is the choice which results in the lowest cost per mont.


Sample problem

Available options

Suppose our protagonist currently owns a Mitsubishi Pajero. He drives approximately 1500 km in a month, and a car salesperson has quoted him a resale value of $3,000 for the car. This car consumes 0.11 liters of petrol per km travelled. (Case 1)

He is considering buying a used Toyota Prius, which sells for $10,000 and has a published fuel consumption rate of 0.05 liters of petrol per km travelled. (Case 2)

Alternatively, a Honda Accord is available for $4500, and consumes 0.08 liters of petrol per km travelled. (Case 3)

The capital market rate of return, i, and the price of fuel, p, is not known.

Cost functions

Z₁ = 1500×0.11p
Z₂ + (10000-3000)[(1+i)^1/12 - 1]
Z₃ = 1500×0.08p + (4500-3000)[(1+i)^1/12 - 1]
As discussed above, the cost function for each case is the cost of fuel and the lost opportunity to invest in capital markets. Case 1 does not involve opportunity cost as no additional outlays are required.

Solution method

A brute force approach will be used here, as this method allows a large number of cases to be considered. It goes without saying that a spreadsheet program will be most helpful.
The cost functions for all cases are evaluated for a set of possible values of p and i.


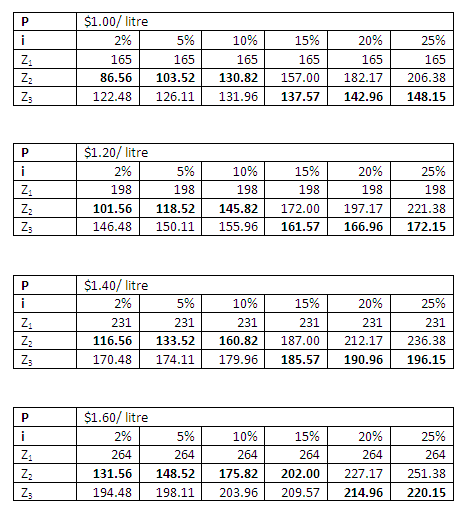
The series of tables show the cost of making each choice for different combinations of fuel price and market rate of return. In this solution, the optimum choice (least expensive) is Case 2 if the market rate of return is expected to be low, and Case 3 if the market rate of return i is expected to be high.


Choosing a non-optimum choice

In some cases, the user may have non-monetary preferences. For example, the protagonist may have a slight dislike for the Toyota Prius because of the perception that only hippies and tree hugging Hollywood-types will want one of these cars.

As it turns out, the Toyota Prius (case 2) was found to be least costly in situations where i is low. In such situations, choosing case 3 instead of case 2 means the user will have to spend more than absolutely necessary.

How much extra are you willing to pay to choose a non-optimal choice? If p = 1.60 and i = 5%, the cost Z₂ is 149 while the cost Z₃ is 198. Are you willing to pay an extra $49 per month just to escape the tree-hugging image of a Toyota Prius?

Good grief, I am getting fat!

No more walking to work/ camera mall/ wet market/ supermarket/ train station/ dinner, a well stocked fridge at home, lots of Milo at work¹ and easily accessible good food are contributing factors to this worryingly tightening waistline. Which is bad, because new pants cost money.

I need more physical activity than what my weekly 2 hours of prancing-about at taekwondo offers.


***

Over the weekend, I dropped by in Singapore (again). I've visited more malls in Singapore than I have in Malaysia and China combined². As a naïve and impressionable person, I was thoroughly in awe of the variety atriums I saw. Most memorable were the 6-storey high and irregularly shaped atrium at Raffles City topped by a seemingly open-air retail space at the top level, and the squarish triple-height atrium at Marina Square was beautifully lit with numerous white coloured deep concrete beams spanning the space diffusing direct sunlight that came in through the glass roof.

On Saturday, we had brunch with 2 of my mother’s schoolday friends, and dinner with my godsister and aunt's family. As is typical for dinners at this aunt's place, it was mind blowing- this uncle is really, really into cooking. Starter was a course of carbonara linguine, followed by a salad with feta cheese and chorizo. This was then followed by a break from eating, after which was the main course. Baked cod fillet wrapped with a thin slice of bacon, served with a dollop of wasabi-tinged mashed potato and portobello mushrooms. Another short break later, we had dessert consisting of D24 durian, jam tarts and cup cakes. The entire process was lubricated with 2 bottles of white wine and talk about food.

Mind blowing indeed.


Notes:
1 I might be over exploiting the free beverages at work. I typically make a very potent cup of Neslo consisting of 4 heaped teaspoons of Milo, 1.5 heaped teaspoons of instant coffee and 1.5 heaped teaspoons of creamer.
2 Likely because most spots of interest are located in, or need to be accessed via an MRT station under a mall of some sorts.

I have resumed taekwondo training after six years of enforced abstinence. Of course, it was not complete deprivation from martial arts through those years. Until a couple of years ago, I had been dabbling in aikido, karate and pseudo-boxing (the fitness kind with no killing intent) to keep myself busy.

On re-entry a month ago, I was pleasantly surprised to find that despite a nasty decline in speed and stamina, I still had a decent grasp of the fundamental skills. In other words, I can still kick, slowly.

On hearing of an upcoming test in November, I asked the instructor if I would be able to make it. “Train for it first, then see if you’re ready later.” Sounds good. I got my black belt in late 2000, 2.5 years after starting as a white belt. My nine-year interval between 1st dan and 2nd dan tests is nine times the wait for a typical practitioner.

For the breaking part of the test, I’m leaning towards using the chopping kick for one of the techniques. Inherently less powerful than a sidekick¹, it will be a suboptimal choice if not for the fact that it’s quite satisfying.



Notes:
1. A sidekick is potentially powerful because it is a very linear kick, with the kicker’s body, the kicking direction, and the target all arranged in a straight line. The reaction force of the kick thrusts horizontally against the kicker’s body, therefore allowing the kicker to use his/her body mass to great advantage.

Hydrodynamics for noobs

Seeing that my work load is particularly low today, I’ll attempt to clarify some fundamental concepts regarding the flow of water¹ through pipes and fittings.

A very fundamental notion to understand in hydraulics is the relationship between flow speed and pressure. A partially blocked pipe will be used to illustrate this relationship.



In this example, the pressure on the left, P_L, is greater than the pressure on the right, P_R. This pressure difference will accelerate water through the blockage, from left to right. As the speed of water flow increases, friction also increases. This friction force is proportional to the square of velocity: doubling the velocity results in four times the friction; tripling the velocity results in nine times the friction.
The flow of water will continue to increase until such a flow speed where the pressure difference, P_L - P_R is balanced by the friction of water rushing through the narrow blockage.

Instead of expressing the friction/ flow resistance as a friction force, it is commonly expressed as a pressure difference between the upstream and downstream areas, as a function of flow speed.

ΔP = kV²

This approach to expressing flow resistance is very convenient for practical problems. For example, one may wish to pump a certain volume of water through a valve into a water tank. If the desired flow speed V is known, and the valve’s value of k is known, the pressure difference between the valve’s front and back can be determined. Knowing the pressure inside the water tank, the pressure before the valve needs to be greater than the tank’s pressure by ΔP. This approach also can be used if there are several valves: the pressure difference across the valves can be added together to find out the total pressure loss that occurs when water flows through the system.


What happens when you open a valve in a water tap?

For simplicity, we will assume the water source for a tap is at a constant pressure, and the tap opens out to atmospheric pressure. This is quite a reasonable assumption, especially if the tap is connected directly to a water tank with very minimal lengths of piping.

As is the case for water taps, opening the valve allows water to flow out of the tap. Water flows from the high pressure side through the valve and out to the low pressure side. The flow speed is limited by the tap’s flow resistance k.

As shown above, the flow speed and pressure difference is related by ΔP = kV². Given that the pressure difference does not change, the only way to regulate the quantity of water coming out of the tap is by changing k. This happens when the valve is opened or closed. When the valve is closed, k increases (completely closed, the value of k is infinity- there is zero flow even when pressure difference is a finite quantity). When the valve is opened, k decreases.

Notes:
1. or any other viscous and incompressible fluid