An alternative interpretation of the measurement problem found in quantum mechanics
Assumed knowledge:
Some familiarity with Young’s double-slit experiment and quantum mechanical implications of the results.
One very fundamental problem in quantum mechanics is the ‘measurement problem’, in which the act of measurement itself is destroys interesting quantum effects.
The simplest example is using the two-slit experiment. The wave-like nature of light means that constructive and destructive interference result in the familiar fringes of light and dark bands.
If the light source’s intensity is reduced such that only photon is in the system at anyone time, as photon hits accumulate on the detector, the same fringes emerge. The obvious questions at this point are, "how is one photon interfering with itself? Did it go through both slits at the same time?"
Light detectors are then installed behind each of the slits, the objective being to identify which slit the photon actually went through. Unfortunately, and mysteriously, the interference pattern disappears.
Oftentimes, the explanation for this phenomenon is presented by invoking the Heisenberg Uncertainty Principle. On the other hand, Von Neumann and Weigner believed that it was the conscious observation that resulted in the collapse of a wavefunction. Still other interpretations claim that the experimental apparatus itself is part of the experiment, and the results show what the apparatus was designed to show: the wave-like or particle-like nature of light. The many-worlds interpretation raised by Everett is so radical that it is difficult for me to write his proposition succinctly.
However, I personally feel that these do not address the problem satisfactorily, and have developed a handwaving interpretation of my own, based on interactions and wavefunction collapse and reformation.
It would be appropriate to first describe the wavefunction in a general manner. In a handwaving way of explaining it, the wavefunction of a particle is a function that describes the probability of finding the particle in a particular location in space(time).
A wavefunction is said to collapse when the particle's position is 'revealed', so that it's position is no longer a probability distribution, but a definite point in space(time). At that moment, the probability of finding that particle is zero everywhere except where the particle is located.
We will now construct the experimental apparatus by considering the simplest case and incrementally adding elements of complexity to it to finally arrive at the double-slit set up with photodetectors.
A light source, an opaque card (of sufficient thickness to prevent tunnelling effects) and a detector screen are arranged as in the double-slit experiment. However, the opaque card has no slits. All the light that is directed towards the card falls on the card’s surface.
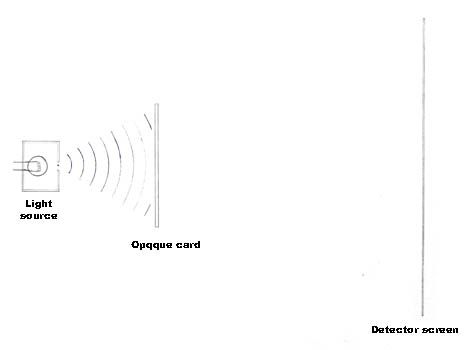
Figure 1: No slits in the card; all light falls on the card’s surface.
From a wavefunction point of view, the wavefunction gives a probability of a photon striking a particular area of the card. When the photon strikes the (interacts with) card, it does so at one point, and the wavefunction has collapsed into a point at that location.
Also note that the presence of the opaque card has modified the wavefunction such that the probability of the photon striking the detector screen is zero.
A slit is then cut in the card, and we see that while most light falls on the opaque card, some of it hits the detector screen.
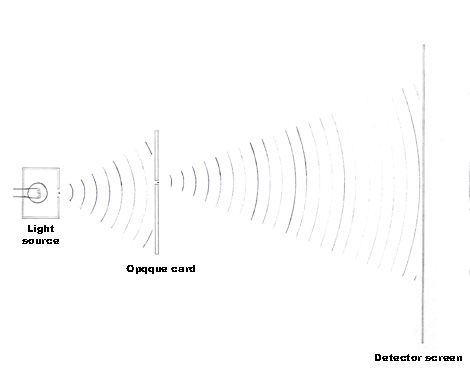
Figure 2: One slit in the card; most light falls on the card's surface, but some reach the detector screen.
As one can see, the probability of finding the photon on the detector screen is no longer zero.
A second slit is cut into the card, and the detector screen shows the typical interference patterns that have become associated with the double-slit experiment.
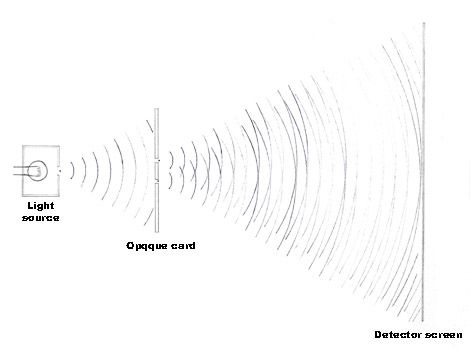
Figure 3: Two slits in the card; most light falls on the opaque card's surface, but the light that falls on the detector screen has alternating light and dark bands that are characteristic to interference.
Photodetectors are then installed at the slits to observe which slit the photon 'actually' went through. The function of these detectors is to alert the experimenter when a photon passes through one of the slits. How the photodetector works is not of interest to us, but we can be sure that the photodetector has to interact with the photon if it is to send a signal that "yes, a photon has passed through."
And here comes the crux of my argument- interactions requires the whole photon’s participation (not merely the probability waves). Thus, only a wavefunction that had collapsed in the detector can produce an entire photon which is capable of interacting with the detector.
Name the photodetectors A and B. If A had sent a signal indicating the passage of a photon, this means that the photon had interacted with A (assuming that A is not faulty). The interaction means that the photon's wavefunction had collapsed into a point in the detector, manifested as the photon (a particle). The wavefucntion's collapse means that the probability of finding this photon on the opaque card or in photodetector B is zero- the photon is definitely in A, and thus definitely not in B nor on the opaque card's surface.
However our photodetectors are designed to allow the photon to proceed on its way to the screen, which means a new wavefunction is produced upon the old one’s collapse. The new wavefunction describes the propogation of a photon from detector A towards the screen. Since the wavefunction of a photon heading towards the screen comes from one source (detector A), there is no interference.
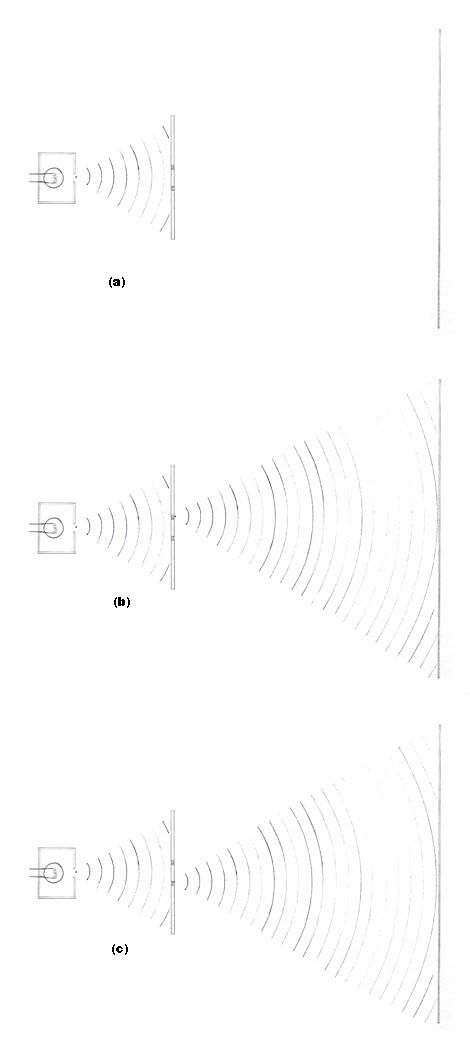
Figure 4:
(a) The photon strikes (interacts with) the opaque card, and the wave function collapses. This photon will never make it to the detector screen.
(b) The photon interacts with photodetector A, and the wavefunction collapses into the detector. The photon then continues on towards the screen, propagating as a new wavefunction originating from detector A.
(c) The photon interacts with photodetector B, and the wavefunction collapses into the detector. The photon then continues on towards the screen, propagating as a new wavefunction originating from detector B.
The interference pattern can also be made to disappear by using only one photodetector behind a slit. In this case, the initial wavefunction is such that there is a probability for the photon to strike the opaque card, strike the detector in the slit, or strike the screen. Any one of these interactions will cause the photon to exist as a particle, and the wavefuction to collapse.
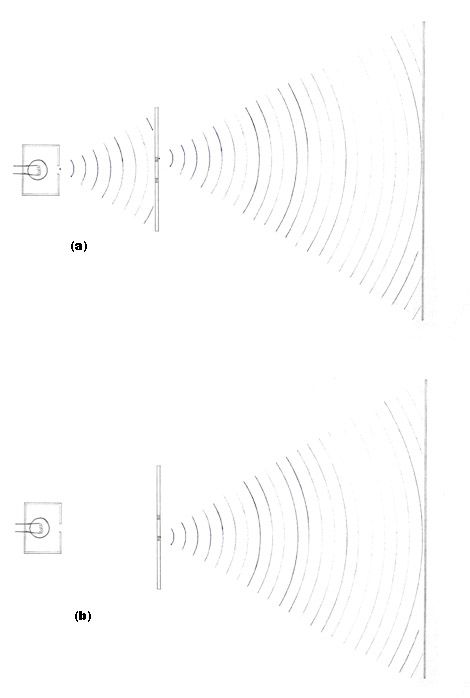
Figure 5:
(a) The initial wavefunction shows that there is a probability for the photon to strike te opaque card's surface (which is not exciting), strike the detector screen (which is interesting) or interact with the photodetector hidden behind the lower slit (which is even more exciting).
(b) If the photon did interact with the photodetector in the lower slit, the initial wavefunction collapses, and a new wavefunction is formed. Note that there is no interference.
Thus the double-slit experiment and measurement problem has been explained by using the argument that an interaction requires the whole particle's presence, which means that the original wavefunction has to collapse, and a new wavefunction to propagate from that point.
It must be noted that the photodetectors behave similarly to the opaque card: it does not allow the wavefunction to have a non-zero value behind it. Hence, a photodetector absorbs photons, just like the opaque card. The difference lies in the fact that the photodetector then spits out that photon after having detected its presence. This new emission event corresponds to a new wavefunction.
Author's note:
Some feedback on the workability of this proposition please? Thank you.
Mr Lee, I'm counting on some sort of response from you.
Mathematics & Applied Sciences
Some familiarity with Young’s double-slit experiment and quantum mechanical implications of the results.
One very fundamental problem in quantum mechanics is the ‘measurement problem’, in which the act of measurement itself is destroys interesting quantum effects.
The simplest example is using the two-slit experiment. The wave-like nature of light means that constructive and destructive interference result in the familiar fringes of light and dark bands.
If the light source’s intensity is reduced such that only photon is in the system at anyone time, as photon hits accumulate on the detector, the same fringes emerge. The obvious questions at this point are, "how is one photon interfering with itself? Did it go through both slits at the same time?"
Light detectors are then installed behind each of the slits, the objective being to identify which slit the photon actually went through. Unfortunately, and mysteriously, the interference pattern disappears.
Oftentimes, the explanation for this phenomenon is presented by invoking the Heisenberg Uncertainty Principle. On the other hand, Von Neumann and Weigner believed that it was the conscious observation that resulted in the collapse of a wavefunction. Still other interpretations claim that the experimental apparatus itself is part of the experiment, and the results show what the apparatus was designed to show: the wave-like or particle-like nature of light. The many-worlds interpretation raised by Everett is so radical that it is difficult for me to write his proposition succinctly.
However, I personally feel that these do not address the problem satisfactorily, and have developed a handwaving interpretation of my own, based on interactions and wavefunction collapse and reformation.
It would be appropriate to first describe the wavefunction in a general manner. In a handwaving way of explaining it, the wavefunction of a particle is a function that describes the probability of finding the particle in a particular location in space(time).
A wavefunction is said to collapse when the particle's position is 'revealed', so that it's position is no longer a probability distribution, but a definite point in space(time). At that moment, the probability of finding that particle is zero everywhere except where the particle is located.
We will now construct the experimental apparatus by considering the simplest case and incrementally adding elements of complexity to it to finally arrive at the double-slit set up with photodetectors.
A light source, an opaque card (of sufficient thickness to prevent tunnelling effects) and a detector screen are arranged as in the double-slit experiment. However, the opaque card has no slits. All the light that is directed towards the card falls on the card’s surface.

Figure 1: No slits in the card; all light falls on the card’s surface.
From a wavefunction point of view, the wavefunction gives a probability of a photon striking a particular area of the card. When the photon strikes the (interacts with) card, it does so at one point, and the wavefunction has collapsed into a point at that location.
Also note that the presence of the opaque card has modified the wavefunction such that the probability of the photon striking the detector screen is zero.
A slit is then cut in the card, and we see that while most light falls on the opaque card, some of it hits the detector screen.

Figure 2: One slit in the card; most light falls on the card's surface, but some reach the detector screen.
As one can see, the probability of finding the photon on the detector screen is no longer zero.
A second slit is cut into the card, and the detector screen shows the typical interference patterns that have become associated with the double-slit experiment.

Figure 3: Two slits in the card; most light falls on the opaque card's surface, but the light that falls on the detector screen has alternating light and dark bands that are characteristic to interference.
Photodetectors are then installed at the slits to observe which slit the photon 'actually' went through. The function of these detectors is to alert the experimenter when a photon passes through one of the slits. How the photodetector works is not of interest to us, but we can be sure that the photodetector has to interact with the photon if it is to send a signal that "yes, a photon has passed through."
And here comes the crux of my argument- interactions requires the whole photon’s participation (not merely the probability waves). Thus, only a wavefunction that had collapsed in the detector can produce an entire photon which is capable of interacting with the detector.
Name the photodetectors A and B. If A had sent a signal indicating the passage of a photon, this means that the photon had interacted with A (assuming that A is not faulty). The interaction means that the photon's wavefunction had collapsed into a point in the detector, manifested as the photon (a particle). The wavefucntion's collapse means that the probability of finding this photon on the opaque card or in photodetector B is zero- the photon is definitely in A, and thus definitely not in B nor on the opaque card's surface.
However our photodetectors are designed to allow the photon to proceed on its way to the screen, which means a new wavefunction is produced upon the old one’s collapse. The new wavefunction describes the propogation of a photon from detector A towards the screen. Since the wavefunction of a photon heading towards the screen comes from one source (detector A), there is no interference.

Figure 4:
(a) The photon strikes (interacts with) the opaque card, and the wave function collapses. This photon will never make it to the detector screen.
(b) The photon interacts with photodetector A, and the wavefunction collapses into the detector. The photon then continues on towards the screen, propagating as a new wavefunction originating from detector A.
(c) The photon interacts with photodetector B, and the wavefunction collapses into the detector. The photon then continues on towards the screen, propagating as a new wavefunction originating from detector B.
The interference pattern can also be made to disappear by using only one photodetector behind a slit. In this case, the initial wavefunction is such that there is a probability for the photon to strike the opaque card, strike the detector in the slit, or strike the screen. Any one of these interactions will cause the photon to exist as a particle, and the wavefuction to collapse.

Figure 5:
(a) The initial wavefunction shows that there is a probability for the photon to strike te opaque card's surface (which is not exciting), strike the detector screen (which is interesting) or interact with the photodetector hidden behind the lower slit (which is even more exciting).
(b) If the photon did interact with the photodetector in the lower slit, the initial wavefunction collapses, and a new wavefunction is formed. Note that there is no interference.
Thus the double-slit experiment and measurement problem has been explained by using the argument that an interaction requires the whole particle's presence, which means that the original wavefunction has to collapse, and a new wavefunction to propagate from that point.
It must be noted that the photodetectors behave similarly to the opaque card: it does not allow the wavefunction to have a non-zero value behind it. Hence, a photodetector absorbs photons, just like the opaque card. The difference lies in the fact that the photodetector then spits out that photon after having detected its presence. This new emission event corresponds to a new wavefunction.
Author's note:
Some feedback on the workability of this proposition please? Thank you.
Mr Lee, I'm counting on some sort of response from you.
Mathematics & Applied Sciences
Labels: natural science, physics

<< Home