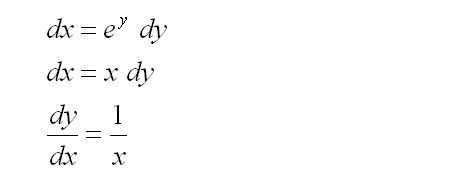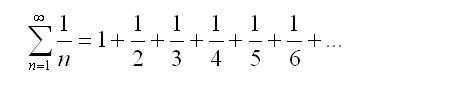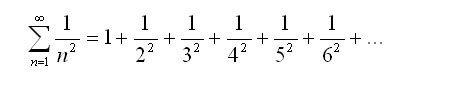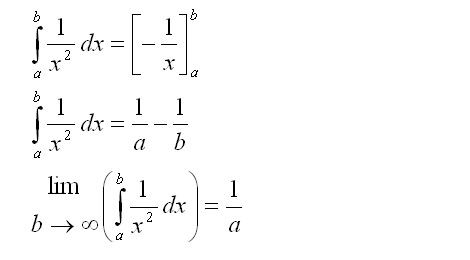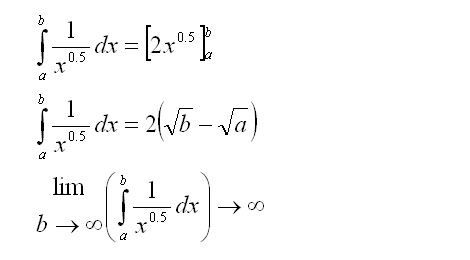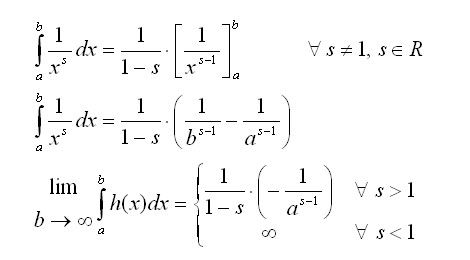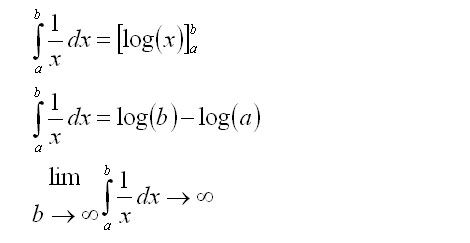The family of series in consideration today is of the following form:

For
s = 1, the series is the harmonic series, which is a (slowly) divergent series.
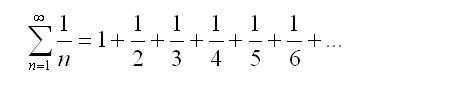
For
s = 2, it is the Basel Problem, named after the Swiss city where Jakob Bernoulli published the problem. Interestingly enough, the Basel problem was originally raised by Professor Pietro Mengoli at the University of Bologna. Regardless, it is referred to as the Basel Problem and not as the “Bologna Problem”. In particular, the Basel Problem is a convergent series, but to exactly what number it converges to, no one knew. 46 years after it was raised, Leonhard Euler found the closed form to the Basel Problem, as well as an algorithm for the closed form for all even numbers of
s. Up to now, there is no known closed form for odd numbers of s.
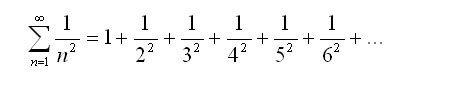
In his investigations of prime numbers, Bernhard Riemann used the above family of series, and called it the Zeta function in his 1859 paper.

The convergence or divergence of the Zeta function can be easily proven using the power of calculus. In particular, the series for a particular
s can be compared to the integral of a suitably chosen function.
Consider the Basel Problem. To show that it is a convergent series, the elements of the series are compared to a continuous function
f(
x).

The comparison itself will consider the area bounded by the series, and area bounded by the function
f. The area of the function
f is simply its integral, while the area of the series is the sum of rectangles of width 1, and of the same height as the series elements.
To show that the series in the Basel Problem is convergent, we first show that
f(
x) is convergent, then fit the series to be always under the function
f(
x), such that the series is always less than or equal to the function
f(
x). Thus if
f(
x) converges, the series converges.
Firstly, show that the integral of
f(
x) to infinity converges.
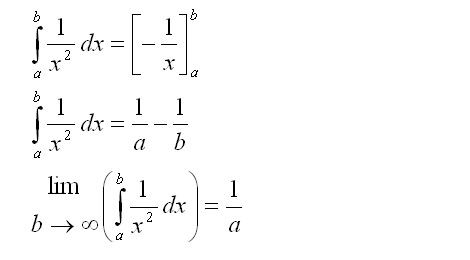
Then, fit the series below the function
f(
x) such that it is always less than or equal to
f(
x).
Integrate from 1 to ∞, and the integral turns out to be one, a finite number.
Note that the integration was not taken from 0 to ∞ because
f(
x) is singular at 0, and we already know that the first term of the series is one, a finite value.
The sum of all terms after the first is strictly less than the integral of
f(
x), since the series is always less than or equal to
f(
x). The integral to infinity is one, and the first term is one. The series should converge to a number less than 1 + 1 = 2. As Euler discovered, it converges to 1.64493…

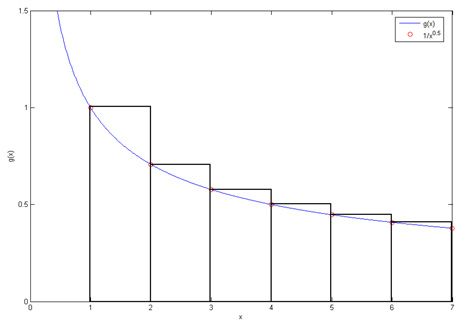
click here for larger imageSimilarly, to show that the Zeta of
s = 0.5 is divergent, all that needs to be done is to compare it to a suitably chosen function
g(
x), and show that the integral of
g(
x) to infinity is divergent. Fit the series so that it is always greater than or equal to
g(
x), so that if the integral of
g(
x) diverges, the series diverges.
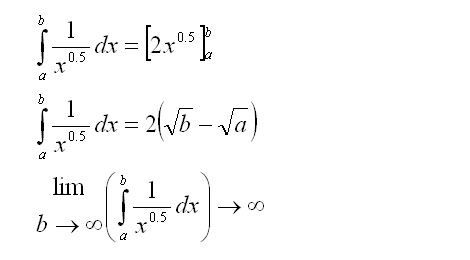
click here for larger imageThe problem is of determining the convergence of the series simply becomes an exercise in integration. For what values of
s does the series converge?
Define a general function to represent the continuous function:

Integrating the
h(
x) from a finite value to infinity, at what values of
s does the integral diverge?
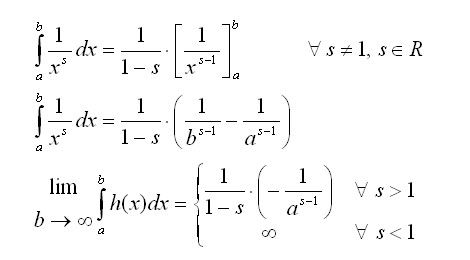
The inverted A symbol represents "for all"
The rounded E symbol represents "is an element of"
The symbol R represents the field of all real numbers
To determine convergence or divergence, the most important criteria is the power of
b (which is the variable that approaches infinity). If
b is raised to a positive power, and then inversed, the value approaches zero and all is well. However, if
b is raised to a negative power and inversed, the value approaches infinity and the series diverges.
Now we know that the series diverges for all
s less than one, and converges for all
s greater than one. And for
s exactly equal to one, the harmonic series:
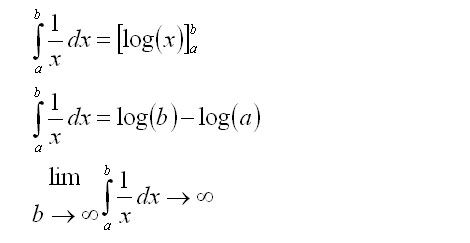
The harmonic series (and the natural logarithm) diverges so amazingly slowly that this phenomenon itself deserves an article.
MathematicsLabels: mathematics, number theory