Saturday, June 28, 2008
Tuesday, June 24, 2008
Random images from Guangzhou
The Chen Clan Academy is a very well preserved home of a well-to-do family bearing the same surname as myself.
It's a huge place, with elaborately sculpted architectural features, large halls, long corridors and spacious courtyards.
A huge rock carving with fantastic 3D detailing was set in the front wall of the mansion.


Click here for large size image
There were many long corridors and doorways:


Click here for large size image

The weather was terrible in Guangzhou. With daytime temperatures of 30 - 36 degrees C and relative humidity of 60 - 90%, we felt like fishes being steamed in a clear, sweaty broth.

Do not be deceived by the pretty rays of sunlight, tufts of clouds and clear blue sky; this is far from heaven.
We got our nails manicured for 20 RMB each. I was extremely disappointed with it. The nails were trimmed, filed and rounded. The cuticles were pushed back and trimmed with a cuticle cutter. A layer of polish was then applied (which I did not opt for).
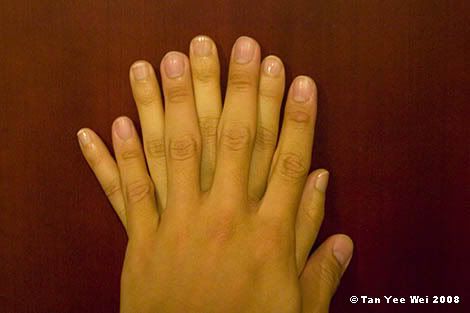
So I paid 20 RMB to get my nails trimmed. Pfft. Where's the emery board and multi-stage buffing? Why aren't my nails ground smooth and then polished to the shine of a brand new PVC bottle?
For RM5 (~10 RMB), I can get myself a nail buffing kit and do it for everyone.
:(
It's a huge place, with elaborately sculpted architectural features, large halls, long corridors and spacious courtyards.
A huge rock carving with fantastic 3D detailing was set in the front wall of the mansion.


Click here for large size image
There were many long corridors and doorways:


Click here for large size image

The weather was terrible in Guangzhou. With daytime temperatures of 30 - 36 degrees C and relative humidity of 60 - 90%, we felt like fishes being steamed in a clear, sweaty broth.

Do not be deceived by the pretty rays of sunlight, tufts of clouds and clear blue sky; this is far from heaven.
We got our nails manicured for 20 RMB each. I was extremely disappointed with it. The nails were trimmed, filed and rounded. The cuticles were pushed back and trimmed with a cuticle cutter. A layer of polish was then applied (which I did not opt for).

So I paid 20 RMB to get my nails trimmed. Pfft. Where's the emery board and multi-stage buffing? Why aren't my nails ground smooth and then polished to the shine of a brand new PVC bottle?
For RM5 (~10 RMB), I can get myself a nail buffing kit and do it for everyone.
:(
Labels: China, holidays, personal, photography
Sunday, June 22, 2008
Beijing Capital International Airport/ Dinner with Jolene Lai/ Guilin photographs
I'm back online!
My absence over the past three weeks can be attributed to a fortnight-long visit back home (to sort out my working visa, not a holiday) and then a week-long holiday in Guangzhou and Guilin with Jean.
From Tianjin, I flew to Kuala Lumpur via Beijing. The new Terminal Three of the Beijing Capital International Airport is mind boggling, jaw droppingly huge. I have seen images and articles about the new terminal, but nothing can prepare one for the shock of actually entering that structure.


Click here for large size image
These two photos were taken about midway along the length of the departure hall.
 \
\
Gate E09 within the satellite building.
I was trying to be cute and hoped to get a photo of E6, but it was E06 so that was not as fun
ps. E-6 is the process used to develop colour slide film.
To get to the boarding gates, passangers take a short train ride to a satellite building (just like in the KLIA). This building is another exercise in collosality.
In the klang valley, I finally met Jolene! She is every bit as interesting as her blogging persona. We took a drive to Klang for some seafood (deep fried butter prawns and peppered clam soup).
For my brother's 21st birthday, mom made some strawberry tarts. A light buttery cup, with a bit of dark chocolate spread around the bottom, then filled with frech custard (home made- not stirred from milk and custard powder; the real stuff is GOOD), and topped with sliced strawberries. The shiny liquid on top is a bit of strawberry jam just to give it a bit of a sheen.

They were heavenly... *swoons*
Last Thursday on the 12th, I took a bus to Singapore (where I managed to persuade a 2 year old with a fearsome reputation for not letting strangers touch him to let me carry him *prouds*), then took a flight to Guangzhou. After a few days in Guangzhou, it was a 45-minute trip in the air and we were in Guilin.

Look at the mountains!
Click here for large size image
Guilin is beautiful. The air is clean, there is lush greenery everywhere (even the grass on the kerbs are beautifully green). Guilin is also famous for its karst landscape, the stuff you see in paintings. It is a little like our own Ipoh (clean and surrounded by lumpy mountains), but much, much more beautiful.

Click here for large size image
Guilin has plenty of fantastic scenery due to the abundence of mountains, greenery and rivers. Unfortunately, it was drizzly and rainy while we were there so we missed out on a lot of those sights. In a way we were fortunate- if we were there one or two days earlier it would not be mere drizzles but torrential downpours. The river's water level rose a good 1.5 m or so those days.
One of the rock formations within Guilin town resembles an elephant dipping its trunk into the river. Not surprisingly, it's named Elephant Trunk Rock.

Click here for large size image
A large, fantastically maintained park surrounds the rock, and the theme of the park is elephant (duh!). There are cute elephant statues you can do all manner of things with:

Click here for large size image

Click here for large size image
Steps are cut into the rock to allow tourists a safe climb up that thing:

There were a few other attractions in Guilin, but with no photographs and a lazy brain (i've lost my muse), we'll just skip those.

Plane(s) of symmetry
Click here for large size image
When we left for Guangzhou, the flight was delayed by about 2 hours due to bad weather in Guangzhou.
My absence over the past three weeks can be attributed to a fortnight-long visit back home (to sort out my working visa, not a holiday) and then a week-long holiday in Guangzhou and Guilin with Jean.
From Tianjin, I flew to Kuala Lumpur via Beijing. The new Terminal Three of the Beijing Capital International Airport is mind boggling, jaw droppingly huge. I have seen images and articles about the new terminal, but nothing can prepare one for the shock of actually entering that structure.


Click here for large size image
These two photos were taken about midway along the length of the departure hall.
 \
\Gate E09 within the satellite building.
I was trying to be cute and hoped to get a photo of E6, but it was E06 so that was not as fun
ps. E-6 is the process used to develop colour slide film.
To get to the boarding gates, passangers take a short train ride to a satellite building (just like in the KLIA). This building is another exercise in collosality.
In the klang valley, I finally met Jolene! She is every bit as interesting as her blogging persona. We took a drive to Klang for some seafood (deep fried butter prawns and peppered clam soup).
For my brother's 21st birthday, mom made some strawberry tarts. A light buttery cup, with a bit of dark chocolate spread around the bottom, then filled with frech custard (home made- not stirred from milk and custard powder; the real stuff is GOOD), and topped with sliced strawberries. The shiny liquid on top is a bit of strawberry jam just to give it a bit of a sheen.

They were heavenly... *swoons*
Last Thursday on the 12th, I took a bus to Singapore (where I managed to persuade a 2 year old with a fearsome reputation for not letting strangers touch him to let me carry him *prouds*), then took a flight to Guangzhou. After a few days in Guangzhou, it was a 45-minute trip in the air and we were in Guilin.

Look at the mountains!
Click here for large size image
Guilin is beautiful. The air is clean, there is lush greenery everywhere (even the grass on the kerbs are beautifully green). Guilin is also famous for its karst landscape, the stuff you see in paintings. It is a little like our own Ipoh (clean and surrounded by lumpy mountains), but much, much more beautiful.

Click here for large size image
Guilin has plenty of fantastic scenery due to the abundence of mountains, greenery and rivers. Unfortunately, it was drizzly and rainy while we were there so we missed out on a lot of those sights. In a way we were fortunate- if we were there one or two days earlier it would not be mere drizzles but torrential downpours. The river's water level rose a good 1.5 m or so those days.
One of the rock formations within Guilin town resembles an elephant dipping its trunk into the river. Not surprisingly, it's named Elephant Trunk Rock.

Click here for large size image
A large, fantastically maintained park surrounds the rock, and the theme of the park is elephant (duh!). There are cute elephant statues you can do all manner of things with:

Click here for large size image

Click here for large size image
Steps are cut into the rock to allow tourists a safe climb up that thing:

There were a few other attractions in Guilin, but with no photographs and a lazy brain (i've lost my muse), we'll just skip those.

Plane(s) of symmetry
Click here for large size image
When we left for Guangzhou, the flight was delayed by about 2 hours due to bad weather in Guangzhou.
Labels: China, holidays, photography
Friday, June 06, 2008
It seems that I have made a difference in the universe. While not a massive feat, it's definitely non-trivial.
The god-sister wrote:
The god-sister wrote:
As I plump myself into the back seat of my friend’s car on the way home from tuition and with my left cheek touching the cold surface of the car’s window, I thought about the boring-to-you-yet-interesting-to-me identity numbers. This was passed down to me by my great mathematics teacher who also happens to be my god brother, Tan Yee Wei (aka the Pink Man).
[Future reference for self when I get amnesia: Identity numbers are numbers that leave another number unchanged when an operation is applied. Yeah, I think that’s what he said. It seems so much less magical now that I’ve learnt in school. But a few years back when algebra was foreign to me, it was simply fascinating. He told me that the identity of addition (and subtraction) operations is 0 whereas the identity number for multiplication (or division) is 1. It’s simple really, if you add any number by 0, or subtract for that matter, you get the same number, thus 0 is the identity. And if you multiply or divide a number by 1, you’d also find yourself with the same number you started off with. Cool eh? Yes. I’m a dweeb. And come to think about it, I still find it quite fascinating. I mean, who would ever think about that sort of things?]
Well, that gave me a jump-start and got my mind churning. I realise that I have this hunger for knowledge. I love to inquire as I feast on information. As a matter of fact, I tend to be in favour of self-realizations. Likewise, I find myself always wanting to be the best that I can be.
Labels: mathematics, personal
Monday, June 02, 2008
Beauty in an ordered set plantation
When driving along large, well ordered plantations, one often notices that the trees appear to line up in straight lines when one looks in different directions. The simplest example will be using a square grid as follows:
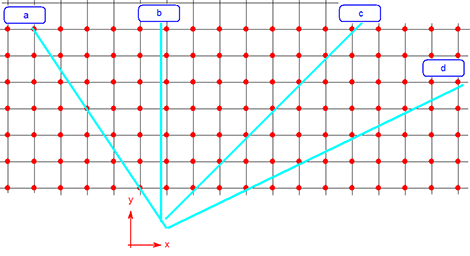
As the observer looks along the directions a, b, c, and d, he sees neat rows where tree trunks lined up. The directions a, b, c and d can start to make more sense when we express the gradient of the lines-of-sight:
We start with line d, for that is the simplest to explain:

This is derived by observing that y increases by one step when x increases by 2 steps. Similarly, the gradients for the other lines are:
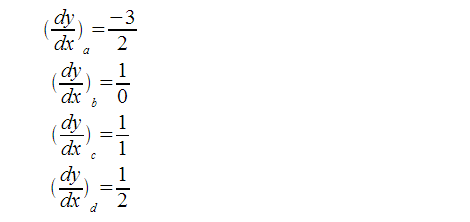
The above shows that lines of sights with integer numerators and integer denominators will have ordered rows of trees. However, it should be noted that 2/2 is equal to 1/1, thus some integer-pairs need to be eliminated. This can be done by dividing both the numerator and denominator by all their common factors. In other words, the numerator and denominator is to be relatively-prime.
At this point, the argument is starting to look remarkably similar to the well known problem of “how many rational numbers are there?” The answer is infinity.
Thus, in an infinitely large plantation with trees of infinitesimally narrow trunks (this is a necessary condition to prevent other trees' trunks from blocking the line of sight), there are infinitely many lines of sights that result in orderly lines. Of course, it is naturally assumed that in this odd plantation, the spacing and arrangement of trees are perfectly regular.
The strength of the visible trend line of lined-up trees depends on how far one needs to move along the line of sight before another tree is sighted. In other words, the visibility of the trend line is dependent on the linear density of the trees along the line of sight.
The packing density can be inferred by the numerator and denominator of the gradient (when already expessed as relatively-prime numbers). The separation distance of trees along the line of sight is simply the hypotenuses of the triangle consisting of the perpendicular sides of lengths [numerator] and [denominator]. The separation distance is thus:

Thus, for a line of sight to be a very obvious one, both x and y must be small to result in more trees occurring along the line of sight. This is consistent with general observations in the field that the line of trees along the line of sight b is more obvious than the line along c, which is more obvious than along d, which is more obvious than along a.
This approach to analysis can apply to non-orthogonal layouts as well. For example, if the grid was deformed as follows, the analysis above still applies.
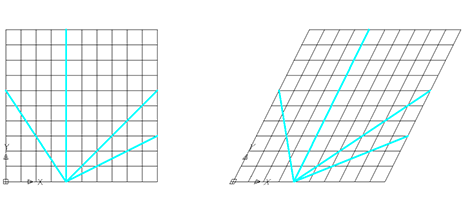
However, inference of the strength of the trend line requires explicit coordinate manipulation to determine the exact inter-tree spacing (the equation of s=sqrt (x^2 + y^2) does not apply for non-orthogonal x and y).
If the plantation was arrayed in a hexagonal/triangular layout (which allows the greatest packing density of trees), the above analysis can still be used. (note: in this arrangement, trees can be the vertices of the triangles, of the the centres of hexagons. This is illustrated below)
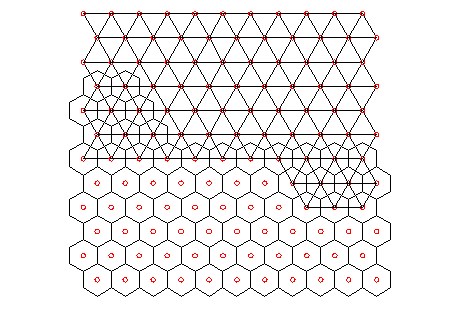
The hexagonal/triangular layout can be recast as a deformed square (properly called a parallelogram), as shown below:
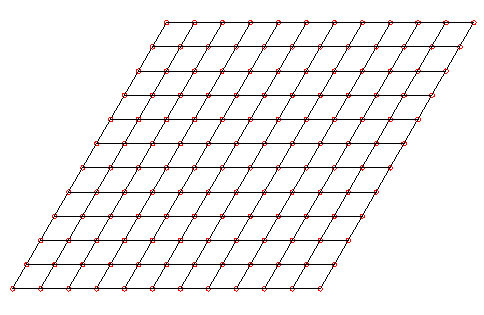

As the observer looks along the directions a, b, c, and d, he sees neat rows where tree trunks lined up. The directions a, b, c and d can start to make more sense when we express the gradient of the lines-of-sight:
We start with line d, for that is the simplest to explain:

This is derived by observing that y increases by one step when x increases by 2 steps. Similarly, the gradients for the other lines are:
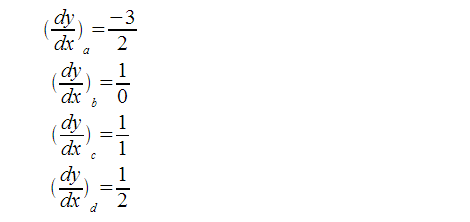
The above shows that lines of sights with integer numerators and integer denominators will have ordered rows of trees. However, it should be noted that 2/2 is equal to 1/1, thus some integer-pairs need to be eliminated. This can be done by dividing both the numerator and denominator by all their common factors. In other words, the numerator and denominator is to be relatively-prime.
At this point, the argument is starting to look remarkably similar to the well known problem of “how many rational numbers are there?” The answer is infinity.
Thus, in an infinitely large plantation with trees of infinitesimally narrow trunks (this is a necessary condition to prevent other trees' trunks from blocking the line of sight), there are infinitely many lines of sights that result in orderly lines. Of course, it is naturally assumed that in this odd plantation, the spacing and arrangement of trees are perfectly regular.
The strength of the visible trend line of lined-up trees depends on how far one needs to move along the line of sight before another tree is sighted. In other words, the visibility of the trend line is dependent on the linear density of the trees along the line of sight.
The packing density can be inferred by the numerator and denominator of the gradient (when already expessed as relatively-prime numbers). The separation distance of trees along the line of sight is simply the hypotenuses of the triangle consisting of the perpendicular sides of lengths [numerator] and [denominator]. The separation distance is thus:

Thus, for a line of sight to be a very obvious one, both x and y must be small to result in more trees occurring along the line of sight. This is consistent with general observations in the field that the line of trees along the line of sight b is more obvious than the line along c, which is more obvious than along d, which is more obvious than along a.
This approach to analysis can apply to non-orthogonal layouts as well. For example, if the grid was deformed as follows, the analysis above still applies.

However, inference of the strength of the trend line requires explicit coordinate manipulation to determine the exact inter-tree spacing (the equation of s=sqrt (x^2 + y^2) does not apply for non-orthogonal x and y).
If the plantation was arrayed in a hexagonal/triangular layout (which allows the greatest packing density of trees), the above analysis can still be used. (note: in this arrangement, trees can be the vertices of the triangles, of the the centres of hexagons. This is illustrated below)

The hexagonal/triangular layout can be recast as a deformed square (properly called a parallelogram), as shown below:

Labels: applied mathematics, mathematics
