The JFE 8555 problem explained
Continuing from the previous entry:
The key to unravelling this problem lies in the number 9. What is so special about this number?
We’ll first consider the numbers 10, 100 and 1000.
10 = 9 +1
100 = 99 + 1
1000 = 999 + 1
Divide the numbers by 9:
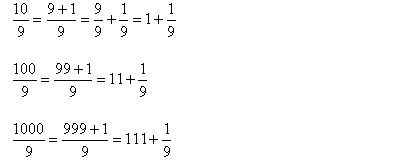
The interesting point about this division operation is that there is a remaining fraction 1/9.
The following example (using 35897) should make it obvious that this division by 9 is analogous to digit extraction where we extract digits out of a multi-digit number.
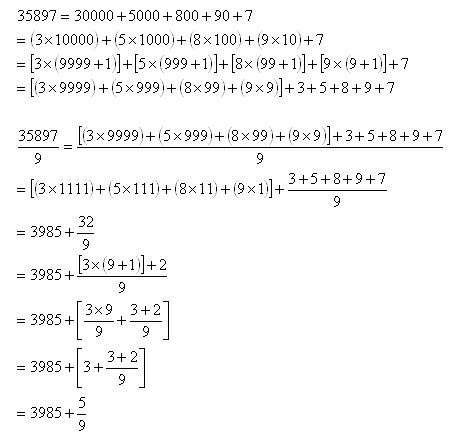
And out of this mess comes 5 as the numerator in the fraction.
So the above case was an illustration of
35897
3 + 5 + 8 + 9 + 7 = 32
-> 3 + 2 = 5
Can we do it for the following?
35897
3 + 58 + 97 = 158
-> 15 + 8 = 23
-> 2 + 3 = 5
This time, the digits have been arbitrarily condensed into groups.
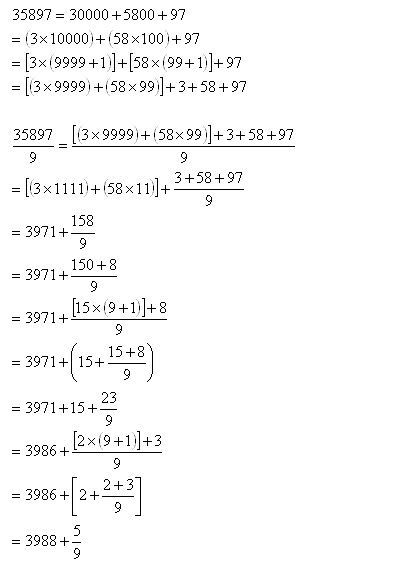
Again, 5 appears at the end of the digit summation operation. 5 always appears, because the digit summation operation is simply showing part of the divide by 9 process. And, 35897 divide by 9 will always give 3988 + 5/9 no matter how you express the individual components.
Mathematics
We will attempt to add the digits together in any arbitrary manner, repeating till we reach one digit.
35897
-> 3 + 5 + 8 + 9 + 7 = 32
-> 3 + 2 = 5
(35) + (897) = 932
-> 9 + 3 + 2 = 14
-> 1 + 4 = 5
(3+5) + (8 + 9) + 7 = (8) + (17) + 7
-> 8 + (1+7) + 7 = 8 + 8 + 7
-> 8 + 8 + 7 = 23
-> 2 + 3 = 5
3 + 58 + 97 = 158
-> 15 + 8 = 23
-> 2 + 3 = 5
The flabbergasted reader might want to try a few other combinations for amazement’s sake, and to show that the result is always 5.
The key to unravelling this problem lies in the number 9. What is so special about this number?
We’ll first consider the numbers 10, 100 and 1000.
10 = 9 +1
100 = 99 + 1
1000 = 999 + 1
Divide the numbers by 9:
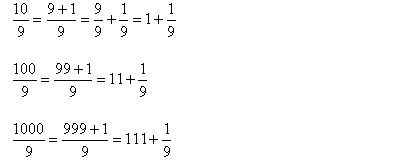
The interesting point about this division operation is that there is a remaining fraction 1/9.
The following example (using 35897) should make it obvious that this division by 9 is analogous to digit extraction where we extract digits out of a multi-digit number.
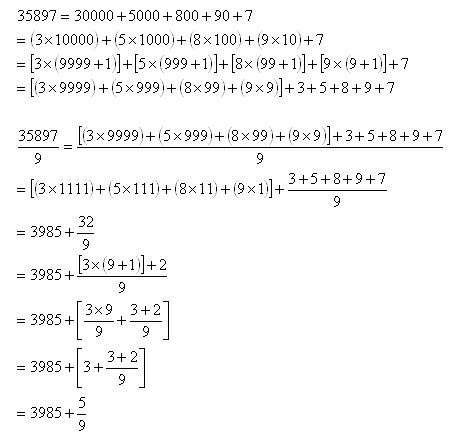
And out of this mess comes 5 as the numerator in the fraction.
So the above case was an illustration of
35897
3 + 5 + 8 + 9 + 7 = 32
-> 3 + 2 = 5
Can we do it for the following?
35897
3 + 58 + 97 = 158
-> 15 + 8 = 23
-> 2 + 3 = 5
This time, the digits have been arbitrarily condensed into groups.
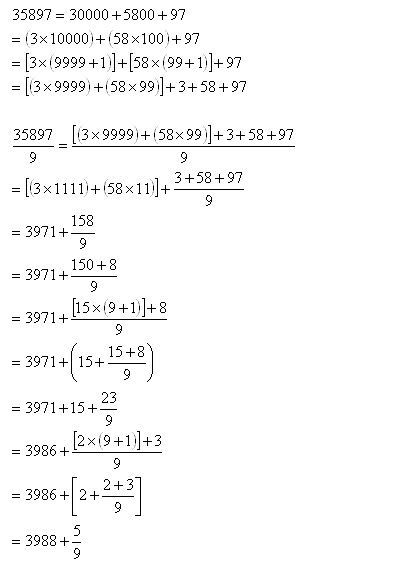
Again, 5 appears at the end of the digit summation operation. 5 always appears, because the digit summation operation is simply showing part of the divide by 9 process. And, 35897 divide by 9 will always give 3988 + 5/9 no matter how you express the individual components.
Mathematics
Labels: mathematics, number theory

<< Home