The apparent ease of divisibility of numbers using different bases: a graphical approach
Most, if not all of us are familiar with the base-10 notation of numbers, where ten symbols are used to represent numbers. These tem symbols are as follows:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
With only ten symbols, we need the represent the infinitely many numbers that we can possibly come across. Hence, several symbols are strung together to represent larger numbers. After nine (‘9’), we are already out of symbols, so we add an additional digit (‘1’) and return the first digit to ‘0’. Thus, the number after nine is represented by ‘10’. The last symbol is then incrementally advanced until we run out of symbols, and the next digits advanced by one symbol. When the second digit reaches the last symbol ‘9’, a third digit is added, and thus the number after ninety-nine (‘99’) is represented using three digits (‘100’).
The natural numbers expressed in base-10 would look like:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22…
History is such that the base-10 system spread to Europe and persisted. In other early cultures, base-5 (one for each finger), base-12 (one for each finger-bone excluding the thumb) and base-60 (the Babylonians used base 60, and this is why the minutes and seconds are in odd 60s.)
If we used base-12, we would need twelve symbols. We shall use
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b
The same set of natural numbers expressed in base-12 would look like:
1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1a…
Returning to the more commonplace base-10 notation, it is easy to see that 6558 can be divided by 2. It is also trivial to see that 6558 cannot be divided by 5. However, it is not as trivial to tell if the same number can be divided by 3.
Using base-10 notation, we can write the numbers in a grid form, such that the width of the grid is ten columns wide.
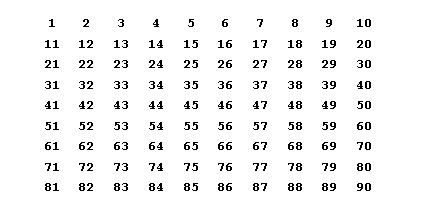
To show the ease of divisibility by two, we will collect the numbers into groups of twos. Numbers that can divide by 2 are marked in red. As the diagram below would clearly show, all the red numbers occur in the same columns. The conclusion is that in base-10, all numbers that end with the symbol of ‘0’, ‘2’, ‘4’, ‘6’ or ‘8’ can be divided by two.
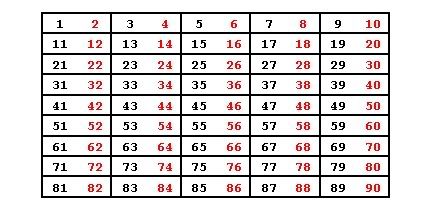
The same can be said of division by five, as the next illustration will show. All base-10 numbers ending with ‘0’ or ‘5’ can be divided by five.
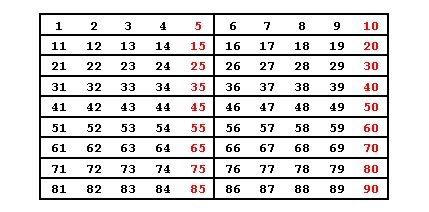
However, three is a tricky one. All numbers that divide by three are spread out over the grid. As such, divisibility cannot be confirmed from the last digit alone.
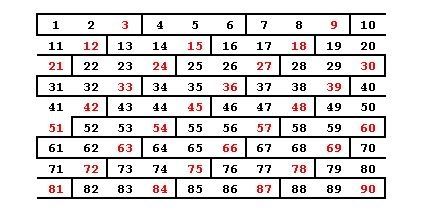
Repeating the same exercise for base-12:
Write the numbers in a grid.

Group numbers together in pairs to check for division by 2.
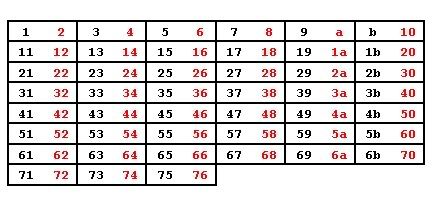
Group numbers together in pairs to check for division by 3.
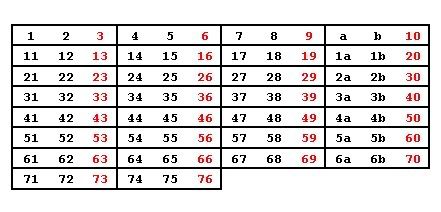
Group numbers together in pairs to check for division by 5.
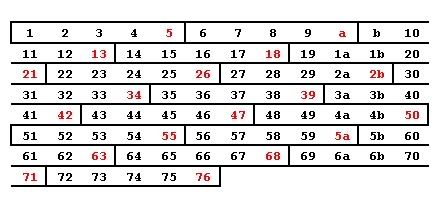
We have seen that divisibility is easy to confirm if the last digit can be used to judge the divisibility. From the above examples, using the last digit as a means of evaluating divisibility is only valid only if the groups of numbers stack exactly on top of one another.
If we write the number in base-n, and wish to divide the number by k, then the stacking occurs if and only if n can be divided by k. For example, 10 can be divided by 2, such that at every new row, the number groupings start from the first number instead of continuing from the previous row (like that seen in base-10, division by 3).
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
With only ten symbols, we need the represent the infinitely many numbers that we can possibly come across. Hence, several symbols are strung together to represent larger numbers. After nine (‘9’), we are already out of symbols, so we add an additional digit (‘1’) and return the first digit to ‘0’. Thus, the number after nine is represented by ‘10’. The last symbol is then incrementally advanced until we run out of symbols, and the next digits advanced by one symbol. When the second digit reaches the last symbol ‘9’, a third digit is added, and thus the number after ninety-nine (‘99’) is represented using three digits (‘100’).
The natural numbers expressed in base-10 would look like:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22…
History is such that the base-10 system spread to Europe and persisted. In other early cultures, base-5 (one for each finger), base-12 (one for each finger-bone excluding the thumb) and base-60 (the Babylonians used base 60, and this is why the minutes and seconds are in odd 60s.)
If we used base-12, we would need twelve symbols. We shall use
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b
The same set of natural numbers expressed in base-12 would look like:
1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1a…
Returning to the more commonplace base-10 notation, it is easy to see that 6558 can be divided by 2. It is also trivial to see that 6558 cannot be divided by 5. However, it is not as trivial to tell if the same number can be divided by 3.
Using base-10 notation, we can write the numbers in a grid form, such that the width of the grid is ten columns wide.

To show the ease of divisibility by two, we will collect the numbers into groups of twos. Numbers that can divide by 2 are marked in red. As the diagram below would clearly show, all the red numbers occur in the same columns. The conclusion is that in base-10, all numbers that end with the symbol of ‘0’, ‘2’, ‘4’, ‘6’ or ‘8’ can be divided by two.

The same can be said of division by five, as the next illustration will show. All base-10 numbers ending with ‘0’ or ‘5’ can be divided by five.

However, three is a tricky one. All numbers that divide by three are spread out over the grid. As such, divisibility cannot be confirmed from the last digit alone.

Repeating the same exercise for base-12:
Write the numbers in a grid.

Group numbers together in pairs to check for division by 2.

Group numbers together in pairs to check for division by 3.

Group numbers together in pairs to check for division by 5.

We have seen that divisibility is easy to confirm if the last digit can be used to judge the divisibility. From the above examples, using the last digit as a means of evaluating divisibility is only valid only if the groups of numbers stack exactly on top of one another.
If we write the number in base-n, and wish to divide the number by k, then the stacking occurs if and only if n can be divided by k. For example, 10 can be divided by 2, such that at every new row, the number groupings start from the first number instead of continuing from the previous row (like that seen in base-10, division by 3).

<< Home