The thermodynamics of waste
On the irreversibility and entropy generation of mixing and wastage
We would start by considering waste material. Waste is typically ‘unusable or unwanted material’ (Oxford). Unusable in that any potential good it might have is already practically exhausted; unwanted when a it is no longer deemed beneficial, although possibly still of some benefit.
An example of waste would be an empty ice-cream tub. While it still contained ice-cream, it was useful because it protected the ice-cream from external elements. When the ice-cream is eaten, the container can still serve its function of separating the inside from the outside. However, the end user does not need another container, and the ice-cream manufacturer would rather commission someone to make new tubs than to retrieve empty ones.
Consider the typical route the unwanted ice-cream tub would take on its way to the landfill. It would first be dumped into a household rubbish bin, where a previously clean ice-cream tub would come into contact with other waste materials such as fruit peel, vegetable roots, decaying leftovers and sanitary pads.
Very loosely, one could say that the entropy of the ice-cream tub has increased. To return it to its original, clean, condition, one would need to give it a vigorous scrub to remove unpleasant substances such as fermenting banana skins and menstrual discharge. The very act of mixing the materials together in a common bin has irreversibly created a dirty tub. Yes, you can clean the tub, but it will cost you some work. Thus the irreversibility.
At some point in the waste disposal process, the rubbish would be crushed and compressed. What was previously an intact but dirty tub would be deformed and possibly ruptured. This is yet another irreversibility in the process- after stomping on the tub, you could possibly restore it to the pre-stomped state, but at the expense of a lot of restoration work. Again, one could say that the entropy of the tub has increased.
So, what are the implications of increasing the entropy of a certain system? Well, the most important point is that it has become less useful. To demonstrate the point, we will have to clean ourselves of the rank of rotting rubbish, and subject ourselves to the culinary delights of a kitchen.
Suppose we have a kilogram of green beans, and a kilogram of red beans. At the moment, the two kinds of beans are separated in individual bowls. The chef can make red bean soup, green bean soup or a two-bean soup.
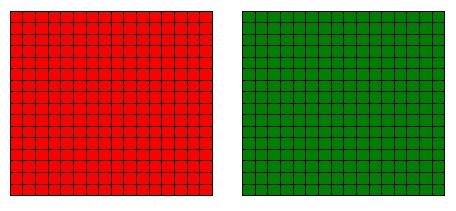
The grid below is a very simplified representation of beans in two bowls. Each cell represents a bean, and its colour represents if it’s a green or red bean. At the moment, the reds are clustered with the reds, and the greens with the greens.
Then suppose an idiot comes along and pours the two different beans together into a big bowl, thoroughly mixing them. Upon seeing this mess, the chef would curse passionately in various languages.
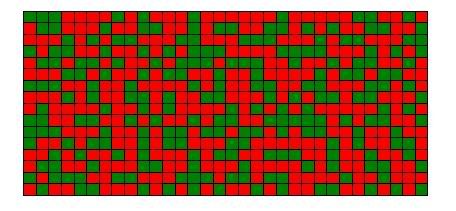
While the chef did lose any beans, he did gain a great deal of entropy. He still can make a two-bean soup, but to make either the red bean or green bean soup would requite some additional effort to remove entropy from the mixed beans. That is, it would mean sorting the beans into reds and greens. Thus, we see the usefulness of the mixed beans has diminished greatly compared to the separated case.
Returning to Boltzmann’s definition of entropy, “entropy is a measure of the number of possible microscopic states (or microstates) of a system, consistent with its macroscopic properties (or macrostate)”. (Wikipedia) What this implies is for our bean mixing exercise is that you can rearrange the individual beans while not changing the overall picture.
For example, consider the unmixed beans. You can take 2 red beans and swap their positions. You have changed the microstate of the system, but on the large scale, nothing has changed- the red beans are still separate from the green beans. Referring to the grid model above, you can swap the positions of any pair of red beans and the system would not change. Our model is a 16 by 16 ‘bowl’ with 256 beans. You can reposition the 256 red beans in 256! = 8.5 x 10^506 unique arrangements, and the system remains the same- red beans in one bowl, green beans in the other. Similarly, you can rearrange the 256 green beans in 256! = 8.5 x 10^506 unique arrangements and the system would stay the same. Collectively, you can rearrange the red and green beans in 256! x 256! = 7.4 x 10^1013 ways and the different beans still remain separate.
What happens when the 2 separate bowls of beans are mixed into a large heap of 512 beans? This time, there is no such thing that the reds have to stay in their half of the system and the greens stay in their own half. Like a diverse nation, they are free to intermingle. Now, you can pick any bean irrespective of colour, and swap their positions without changing the system’s macrostate- the red and green beans remain mixed. How many possible microstates are there in this mixed system? We can reposition 512 beans in 512! = 3.5 x 10^1166 unique positions.
This might not look light much compared to the initial unmixed system, but do bear in mind that the exponent 10^116 implies 1166 trailing zeroes in the figure. The number of possible microstates in the mixed system is larger than the unmixed system by 103 digits.
And we are only talking of 512 beans, not really enough to quell anyone’s hunger.
On a final note, the generation of the mixed grid posed an interesting problem. It was done on Excel’s grids, and I did not really fancy having to click on 256 random boxes and replace their colours. The approach taken was to dot a small region with a random pattern. A wide rectangular section was copied from the region and pasted all over the ‘bowl’ in an arbitrary fashion, with some overlap. Then, a tall rectangular section was copied and pasted randomly over the bowl. The approach took advantage of the fact that random structures are in fact more uniform than orderly structures. If you look at a mixed bowl of beans, they would look the same from all directions. If the beans were separated by some partition, from some directions the green would be on the left; from the other direction, red would be on the left.
References:
Concise Oxford English Dictionary, Tenth Edition
Entropy, Wikipedia
http://en.wikipedia.org/wiki/Entropy
Cite this article as:
Tan Yee Wei(2005), "Thermodynamics of waste", from "Snippets of This and That"
http://vapour-trail.blogspot.com/2005/08/thermodynamics-of-waste.html
Mathematics
We would start by considering waste material. Waste is typically ‘unusable or unwanted material’ (Oxford). Unusable in that any potential good it might have is already practically exhausted; unwanted when a it is no longer deemed beneficial, although possibly still of some benefit.
An example of waste would be an empty ice-cream tub. While it still contained ice-cream, it was useful because it protected the ice-cream from external elements. When the ice-cream is eaten, the container can still serve its function of separating the inside from the outside. However, the end user does not need another container, and the ice-cream manufacturer would rather commission someone to make new tubs than to retrieve empty ones.
Consider the typical route the unwanted ice-cream tub would take on its way to the landfill. It would first be dumped into a household rubbish bin, where a previously clean ice-cream tub would come into contact with other waste materials such as fruit peel, vegetable roots, decaying leftovers and sanitary pads.
Very loosely, one could say that the entropy of the ice-cream tub has increased. To return it to its original, clean, condition, one would need to give it a vigorous scrub to remove unpleasant substances such as fermenting banana skins and menstrual discharge. The very act of mixing the materials together in a common bin has irreversibly created a dirty tub. Yes, you can clean the tub, but it will cost you some work. Thus the irreversibility.
The reader familiar with entropy as approached by Boltzmann might want to consider the number of possible microstates for each of the following case: tub and other domestic refuse separated; tub and other domestic refuse mixed.
At some point in the waste disposal process, the rubbish would be crushed and compressed. What was previously an intact but dirty tub would be deformed and possibly ruptured. This is yet another irreversibility in the process- after stomping on the tub, you could possibly restore it to the pre-stomped state, but at the expense of a lot of restoration work. Again, one could say that the entropy of the tub has increased.
So, what are the implications of increasing the entropy of a certain system? Well, the most important point is that it has become less useful. To demonstrate the point, we will have to clean ourselves of the rank of rotting rubbish, and subject ourselves to the culinary delights of a kitchen.
Suppose we have a kilogram of green beans, and a kilogram of red beans. At the moment, the two kinds of beans are separated in individual bowls. The chef can make red bean soup, green bean soup or a two-bean soup.
The grid below is a very simplified representation of beans in two bowls. Each cell represents a bean, and its colour represents if it’s a green or red bean. At the moment, the reds are clustered with the reds, and the greens with the greens.

Then suppose an idiot comes along and pours the two different beans together into a big bowl, thoroughly mixing them. Upon seeing this mess, the chef would curse passionately in various languages.

While the chef did lose any beans, he did gain a great deal of entropy. He still can make a two-bean soup, but to make either the red bean or green bean soup would requite some additional effort to remove entropy from the mixed beans. That is, it would mean sorting the beans into reds and greens. Thus, we see the usefulness of the mixed beans has diminished greatly compared to the separated case.
Returning to Boltzmann’s definition of entropy, “entropy is a measure of the number of possible microscopic states (or microstates) of a system, consistent with its macroscopic properties (or macrostate)”. (Wikipedia) What this implies is for our bean mixing exercise is that you can rearrange the individual beans while not changing the overall picture.
For example, consider the unmixed beans. You can take 2 red beans and swap their positions. You have changed the microstate of the system, but on the large scale, nothing has changed- the red beans are still separate from the green beans. Referring to the grid model above, you can swap the positions of any pair of red beans and the system would not change. Our model is a 16 by 16 ‘bowl’ with 256 beans. You can reposition the 256 red beans in 256! = 8.5 x 10^506 unique arrangements, and the system remains the same- red beans in one bowl, green beans in the other. Similarly, you can rearrange the 256 green beans in 256! = 8.5 x 10^506 unique arrangements and the system would stay the same. Collectively, you can rearrange the red and green beans in 256! x 256! = 7.4 x 10^1013 ways and the different beans still remain separate.
What happens when the 2 separate bowls of beans are mixed into a large heap of 512 beans? This time, there is no such thing that the reds have to stay in their half of the system and the greens stay in their own half. Like a diverse nation, they are free to intermingle. Now, you can pick any bean irrespective of colour, and swap their positions without changing the system’s macrostate- the red and green beans remain mixed. How many possible microstates are there in this mixed system? We can reposition 512 beans in 512! = 3.5 x 10^1166 unique positions.
This might not look light much compared to the initial unmixed system, but do bear in mind that the exponent 10^116 implies 1166 trailing zeroes in the figure. The number of possible microstates in the mixed system is larger than the unmixed system by 103 digits.
And we are only talking of 512 beans, not really enough to quell anyone’s hunger.
On a final note, the generation of the mixed grid posed an interesting problem. It was done on Excel’s grids, and I did not really fancy having to click on 256 random boxes and replace their colours. The approach taken was to dot a small region with a random pattern. A wide rectangular section was copied from the region and pasted all over the ‘bowl’ in an arbitrary fashion, with some overlap. Then, a tall rectangular section was copied and pasted randomly over the bowl. The approach took advantage of the fact that random structures are in fact more uniform than orderly structures. If you look at a mixed bowl of beans, they would look the same from all directions. If the beans were separated by some partition, from some directions the green would be on the left; from the other direction, red would be on the left.
References:
Concise Oxford English Dictionary, Tenth Edition
Entropy, Wikipedia
http://en.wikipedia.org/wiki/Entropy
Cite this article as:
Tan Yee Wei(2005), "Thermodynamics of waste", from "Snippets of This and That"
http://vapour-trail.blogspot.com/2005/08/thermodynamics-of-waste.html
Mathematics
Labels: applied mathematics, applied science, natural science

<< Home