[mathematics] From another point of view...
Assumed knowledge: minimal
Difficulty: 2/5
Tedium: 1/5
Insight: 3/5
Content adapted from “The Beauty and Zen of Mathematics” seminar by the Melbourne University Mathematics and Statistics Society (MUMS).
The problem presented below is used to highlight an elegant approach to solving a particularly nasty mathematical problem.
a + b + c =100; a, b & c are natural numbers (integers greater than zero)
How many possible solutions are there?
To answer the question, we can try counting the number of solutions.
Fix a = 1:
1 + 1 + 98 = 100
1 + 2 + 97 = 100
1 + 3 + 96 = 100
:
:
1 + 98 + 1 = 100
For a = 1, there are 98 possible solutions. What about for a = 2?
Fix a = 2:
2 + 1 + 97 = 100
2 + 2 + 96 = 100
2 + 3 + 95 = 100
:
:
2 + 97 + 1 = 100
For a = 2, there are 97 possible solutions. What about for a = 3, 4, 5, 6 ... 98?
Without crunching numbers for all possible values of a, the semi-enlightened soul might notice that the number of solutions is
98 + 97 + 96 + … + 2 + 1 = 4851.
There are 4851 solutions.
There is an easier approach.
Consider 100 dots arranged in a line:
o o o o o o o o o o o o … o o
1 + 1 + 98 = 100 (a = 1; b = 1; c = 98) can be represented by grouping the dots into groups of 1, 1 and 98, where the first group is for a, the second for b, and the third for c. The grouping will be done by partitioning the dots:
o | o | o o o o o o o o o o … o o
Similarly, 5 + 2 + 93 = 100 (a = 5; b = 2; c = 93) can be represented by grouping the dots into groups of 5, 1 and 94 as shown:
o o o o o | o o | o o o o o … o o
The problem is now reduced to counting how many ways the 2 partitions can be inserted into the 99 gaps between our hundred dots.
The answer is simply 99 C 2 (read “99 choose 2”) = 4851
Finally, some weird word games from the MUMS magazine:
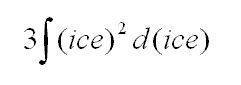
and
The volume of a circular pizza of thickness a and radius z is simply pizza.
Difficulty: 2/5
Tedium: 1/5
Insight: 3/5
Content adapted from “The Beauty and Zen of Mathematics” seminar by the Melbourne University Mathematics and Statistics Society (MUMS).
The problem presented below is used to highlight an elegant approach to solving a particularly nasty mathematical problem.
a + b + c =100; a, b & c are natural numbers (integers greater than zero)
How many possible solutions are there?
To answer the question, we can try counting the number of solutions.
Fix a = 1:
1 + 1 + 98 = 100
1 + 2 + 97 = 100
1 + 3 + 96 = 100
:
:
1 + 98 + 1 = 100
For a = 1, there are 98 possible solutions. What about for a = 2?
Fix a = 2:
2 + 1 + 97 = 100
2 + 2 + 96 = 100
2 + 3 + 95 = 100
:
:
2 + 97 + 1 = 100
For a = 2, there are 97 possible solutions. What about for a = 3, 4, 5, 6 ... 98?
Without crunching numbers for all possible values of a, the semi-enlightened soul might notice that the number of solutions is
98 + 97 + 96 + … + 2 + 1 = 4851.
There are 4851 solutions.
There is an easier approach.
Consider 100 dots arranged in a line:
o o o o o o o o o o o o … o o
-The ellipse shows that the series has been truncated to save on space
1 + 1 + 98 = 100 (a = 1; b = 1; c = 98) can be represented by grouping the dots into groups of 1, 1 and 98, where the first group is for a, the second for b, and the third for c. The grouping will be done by partitioning the dots:
o | o | o o o o o o o o o o … o o
Similarly, 5 + 2 + 93 = 100 (a = 5; b = 2; c = 93) can be represented by grouping the dots into groups of 5, 1 and 94 as shown:
o o o o o | o o | o o o o o … o o
The problem is now reduced to counting how many ways the 2 partitions can be inserted into the 99 gaps between our hundred dots.
The answer is simply 99 C 2 (read “99 choose 2”) = 4851
Finally, some weird word games from the MUMS magazine:
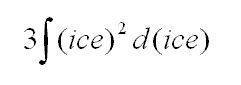
and
The volume of a circular pizza of thickness a and radius z is simply pizza.

<< Home