The derivative of the natural logarithm
Over the past few days, I’ve been puzzling over the derivative of the (natural) log. Why is it 1/x? I could not find a reasonable way to obtain the derivative from first principles.
I gave up, and decided to call upon the power of Google. Here’s how it is done:

Define the (natural) logarithm, and inverse the function to express the variables in an exponential relation.
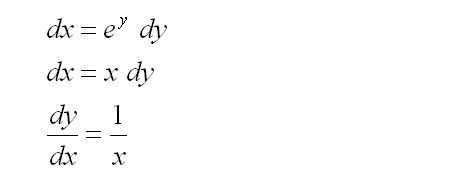
Implicitly differentiate both sides of the exponential function.
Replace the exponential with x, since they are equivalent (from the second equation).
Rearrange to obtain the rate of change of y with respect to x.
It is so absurdly simple I now have a new problem on my hands- why have I not seen this before?
In summary:

Source:
The Derivative of the Natural Logarithm, Math 116, Lake Tahoe Community College Math Department
Mathematics
I gave up, and decided to call upon the power of Google. Here’s how it is done:

Define the (natural) logarithm, and inverse the function to express the variables in an exponential relation.
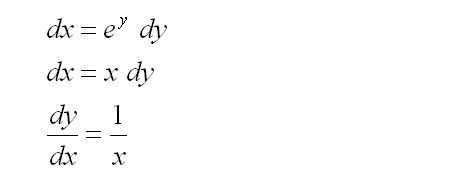
Implicitly differentiate both sides of the exponential function.
Replace the exponential with x, since they are equivalent (from the second equation).
Rearrange to obtain the rate of change of y with respect to x.
It is so absurdly simple I now have a new problem on my hands- why have I not seen this before?
In summary:

Source:
The Derivative of the Natural Logarithm, Math 116, Lake Tahoe Community College Math Department
Mathematics
Labels: mathematics

<< Home