Star Wars Episod II and trigonometry
Of these 2, trigonometry is definitely more interesting.
On Sunday, the second episode of Star Wars was aired on free TV. I was extremely glad I did not bother to pay good money to watch it in the cinema, nor purchase any optical disc (pirated or otherwise) of the said production, nor spend precious time watching the entire film.
The actor for playing the role of Anakin Skywalker was terribly stilted. There were also several clichéd scenes that I thought Lucas should have done without. In a mid-air chase scene, Anakin told his sifu, “Now if you’d excuse me…” and promptly jumped out of the vehicle. The sifu mumbled to himself (and presumably the easily humoured audience), “I hate it when he does that.”
I stopped watching as soon as I was done with dinner. In my defence, I don’t intentionally eat in front of the TV; its just that the living area is in the same room as the dining area AND kitchen. It is plenty of space for 2 students, and not designed for a family with 4 young children.
Back to Star Wars. It appears that almost all vehicular propulsion systems in Star Wars have a certain signature note. This is particularly noticible in the smaller contraptions such as Pod Racers and the vehicle from which stiff Anakin disembarked from.
The signature sound in question consists of a moderate-pitched hum that gets louder and softer in a low frequency.
To try making this sound, start humming. Now, make your humming louder, then soft, then loud, then soft…in a consistent, periodic fashion. (Make sure the pitch does not change) Probably the only difference you will notice is that your hums go up and down much, much slower than what the film shows.
[The following material can get a little intense for individuals who are not mathematically inclined. Knowledge in SPM / O-Level modern mathematics expected.]
Curious about this phenomena, I did some ‘back-of-the-envelope’ calculations by banging some short equations into my favourite GUI (graphic user interface) mathematics problem solver- MathCad.
These are the equations and the corresponding plot:
W1:=200
A1:=5
W2:=201
A2:=6
x(t):=A1*sin(W2*t) + A2*sin(W2*t)
y(t):= cos[(W1-W2)*t]
W is the frequency of oscillation, and A is the corresponding amplitude.
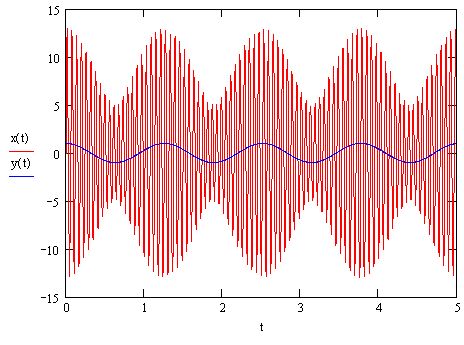
The blue line of y(t) is to illustrate the frequency of amplitude change
Combining 2 separate sinusoids of frequencies 200 and 201 yields a signal of frequency between 200 and 201, and which has an amplitude which goes up and down with a frequency of (201-200) = 1.
This can be easily derived from trigonometric identities (which I did not go through).
And now, we return to the fictitious Star Wars propulsion systems. The hum is audible, and assuming it hums at the musical note of C, it will be at 440 Hz. The amplitude changes at a rate of about 3 Hz. Reconstructing the original signals that generated this signature sound, we can guess that it is of the form:
W1:=441 * 2 pi
W2:=438 * 2 pi
x(t):=A1*sin(W2*t) + A2*sin(W2*t)
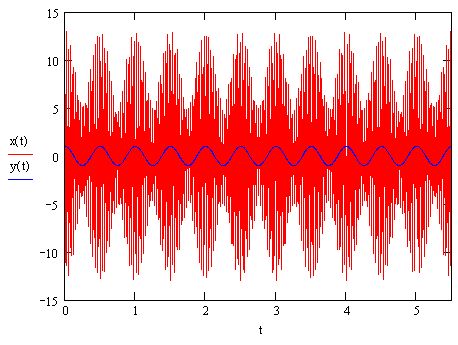
Okay, that’s enough ‘useful’ information for now. Back to work.
On Sunday, the second episode of Star Wars was aired on free TV. I was extremely glad I did not bother to pay good money to watch it in the cinema, nor purchase any optical disc (pirated or otherwise) of the said production, nor spend precious time watching the entire film.
The actor for playing the role of Anakin Skywalker was terribly stilted. There were also several clichéd scenes that I thought Lucas should have done without. In a mid-air chase scene, Anakin told his sifu, “Now if you’d excuse me…” and promptly jumped out of the vehicle. The sifu mumbled to himself (and presumably the easily humoured audience), “I hate it when he does that.”
I stopped watching as soon as I was done with dinner. In my defence, I don’t intentionally eat in front of the TV; its just that the living area is in the same room as the dining area AND kitchen. It is plenty of space for 2 students, and not designed for a family with 4 young children.
Back to Star Wars. It appears that almost all vehicular propulsion systems in Star Wars have a certain signature note. This is particularly noticible in the smaller contraptions such as Pod Racers and the vehicle from which stiff Anakin disembarked from.
The signature sound in question consists of a moderate-pitched hum that gets louder and softer in a low frequency.
To try making this sound, start humming. Now, make your humming louder, then soft, then loud, then soft…in a consistent, periodic fashion. (Make sure the pitch does not change) Probably the only difference you will notice is that your hums go up and down much, much slower than what the film shows.
[The following material can get a little intense for individuals who are not mathematically inclined. Knowledge in SPM / O-Level modern mathematics expected.]
Curious about this phenomena, I did some ‘back-of-the-envelope’ calculations by banging some short equations into my favourite GUI (graphic user interface) mathematics problem solver- MathCad.
These are the equations and the corresponding plot:
W1:=200
A1:=5
W2:=201
A2:=6
x(t):=A1*sin(W2*t) + A2*sin(W2*t)
y(t):= cos[(W1-W2)*t]
W is the frequency of oscillation, and A is the corresponding amplitude.

Combining 2 separate sinusoids of frequencies 200 and 201 yields a signal of frequency between 200 and 201, and which has an amplitude which goes up and down with a frequency of (201-200) = 1.
This can be easily derived from trigonometric identities (which I did not go through).
And now, we return to the fictitious Star Wars propulsion systems. The hum is audible, and assuming it hums at the musical note of C, it will be at 440 Hz. The amplitude changes at a rate of about 3 Hz. Reconstructing the original signals that generated this signature sound, we can guess that it is of the form:
W1:=441 * 2 pi
W2:=438 * 2 pi
x(t):=A1*sin(W2*t) + A2*sin(W2*t)

Okay, that’s enough ‘useful’ information for now. Back to work.

<< Home