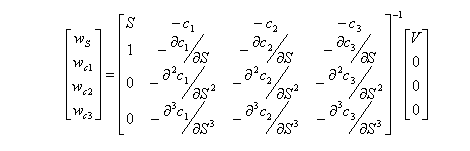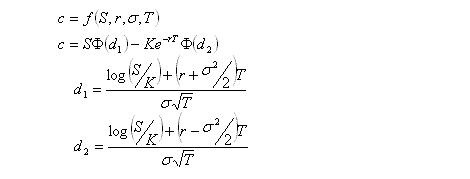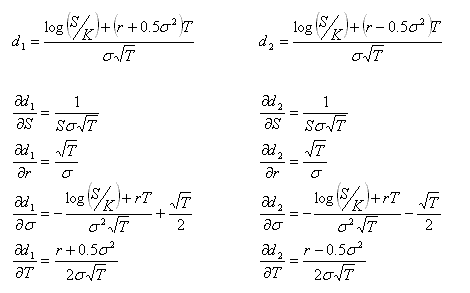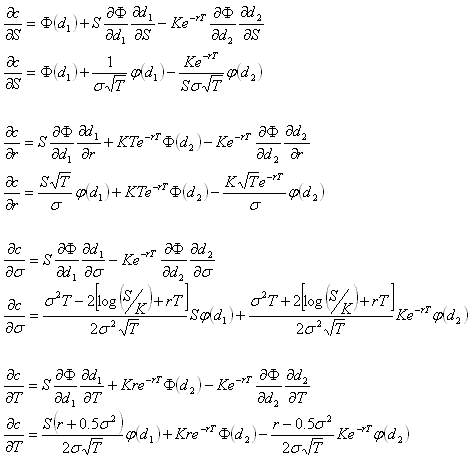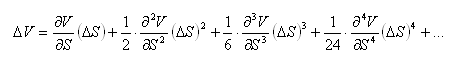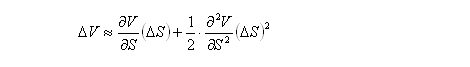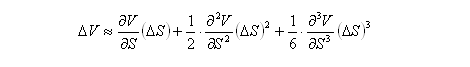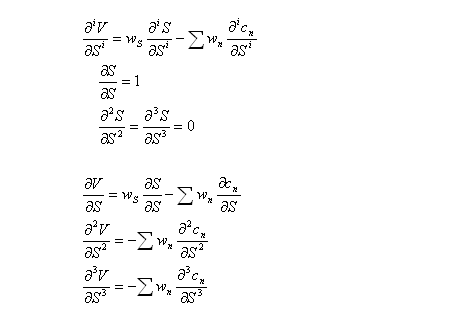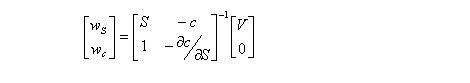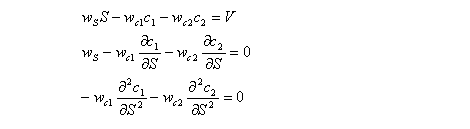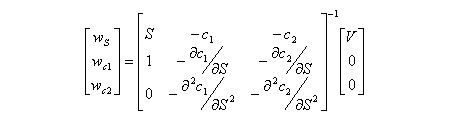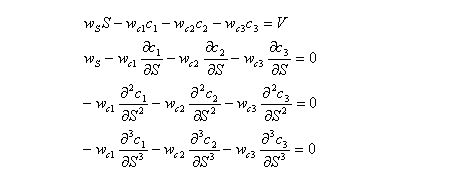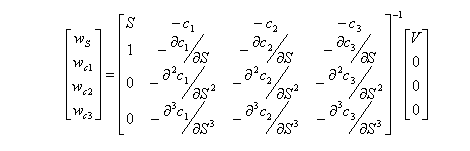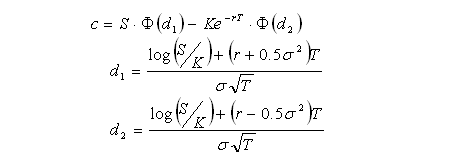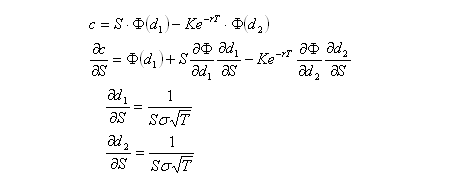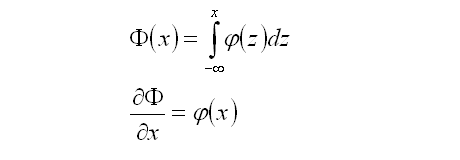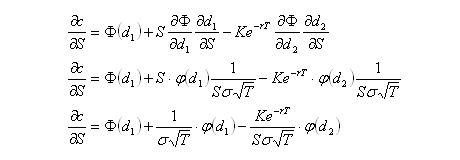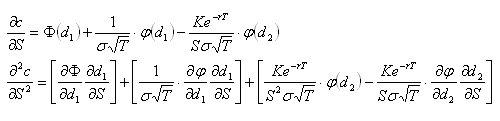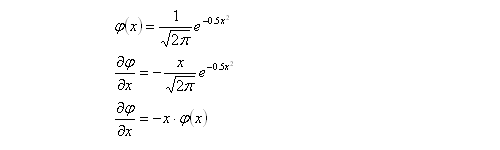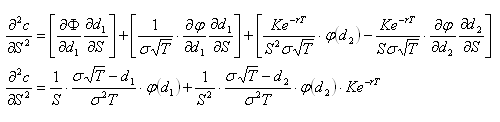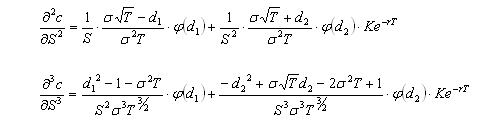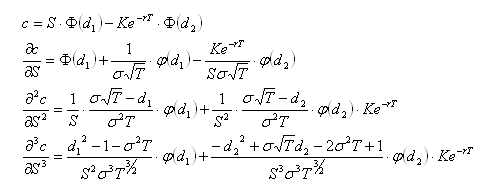Shoes: an experiment in off-camera flash photography

Gradient

Click here for large size image
Super-Takumar 50mm/1.4 exposed at f/8 or thereabouts






Turquoise

Super-Takumar 50mm/1.4 exposed at f/8 or thereabouts

Deriving the first partial derivatives of the Black-Scholes call price equation

Material presented here will be used to discuss hedging strategies to simultaneously hedge an options portfolio against various exposures.

The call option price:


The partial derivatives of d1 and d2:


Partial differentiating c with respect to each variable:


And we're done for today. Easy, no?

Piece by piece, the grand plans for December are falling into place.

Line by line, the set of second partial derivatives for the Black-Scholes call price appear.





Click here for large size image
Super-Takumar 50mm/1.4 exposed at f/5.6

Fire test photographs

Due to the presence of some interesting photographs, I’ll spare you another endless discussion about the mathematics behind options-based hedging.

Today, work (or rather, development at work) brought me to a fire test and training facility where we observed several fires, including a 2m wide pool of heptane (C7H16) fire.



A fascinating one was a room burn, where a stack of wood stick were arranged neatly to optimise combustion. The small room was a 4m × 5 m × 3 m room with only the door as the opening. With a large fire going on in the room and so little ventilation, a portion of the vaporised wood remained unburned and vented out through the door. Once out of the oxygen-depleted environment of the room, the hot fuel vapours immediately oxidised, resulting in flames projecting out of the doorway.




Fire Test

Click here for large size image


Enough about work.

Hedging strategies: a mathematical treatment of delta, delta-gamma, and third-order hedging

Some knowledge of options and delta hedging is required. This post is intended to demonstrate various concepts that will be used in a future post. All price-derivatives of the value of a call option have been derived previously here.


The objective of hedging is to maintain the value of a portfolio in an uncertain market. In hedging against changes in asset prices, a portfolio consisting of options and underlying asset is arranged so that if the value of the asset decreases, the value of the options will increase. The result is a portfolio value that will change by a small amount if the underlying asset price changed.

In today’s analysis, portfolios are created consisting of:
-long positions in the underlying asset, and
-short positions in call options.


The change in value of a portfolio due to a change in the asset price can be expressed as follows:



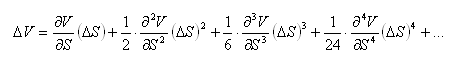
This equation has infinitely many terms, but an approximation can be made by retaining only as many terms as desired. Because the objective of hedging is to maintain the portfolio value constant regardless of any change in S, the following condition needs to be satisfied for all values of i:



In delta hedging, only the first term is retained for accuracy to the first-order:



In delta-gamma hedging, the first two terms are retained for second-order accuracy:



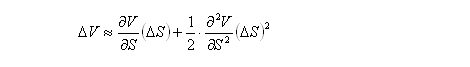
For third-order accuracy,



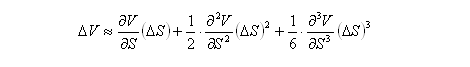
A portfolio consisting of long positions in the underlying asset and short positions in call options would have the following value:

where w corresponds to the quantity of each asset type in the portfolio.



Similarly, the first, second and third derivatives of portfolio value with respect to asset price are:



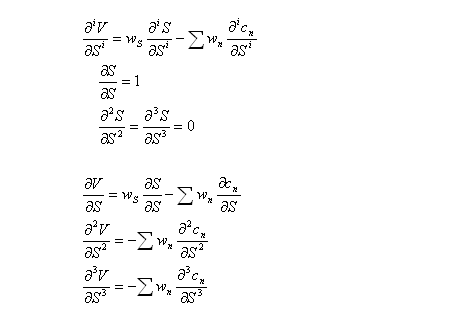Delta hedging
For delta hedging, only one kind of call option is required to hedge the portfolio. The value of the portfolio is to be V, and the weighted sum of first derivatives is to be zero:



Thus, the number of stocks and options to be purchased is the solution to the following matrix equation:



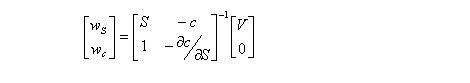Delta-gamma hedging
For delta-gamma hedging, two kinds of call option are required to hedge the portfolio. The value of the portfolio is to be V, and the weighted sums of first and second derivatives are to be zero:



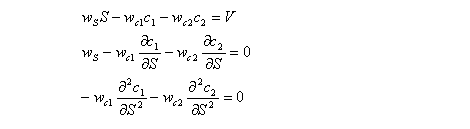
Thus, the number of stocks and options to be purchased is the solution to the following matrix equation:



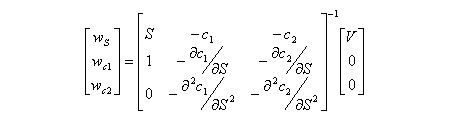Third-order hedging
For hedging to the third order, three kinds of call option are required to hedge the portfolio. The value of the portfolio is to be V, and the weighted sums of first, second and third derivatives are to be zero:



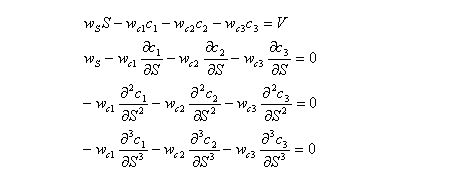
Thus, the number of stocks and options to be purchased is the solution to the following matrix equation:

Deriving the exact equations for Delta, Gamma and the unnamed third price-derivative of a call option

An underlying knowledge of options is assumed. This post is intended to demonstrate various parameters that will be used in a future post.

Using the Black-Scholes model for options pricing, a call option price is:

Where Φ(x) is the cumulative probability function of a standardised normal variable.


Using partial derivatives, the rate of change of c with respect to S will be derived. This rate of change is commonly labelled Δ, Delta.



The normalised probability function and cumulative probability function are related in the following manner:



Substituting this into the partial derivative of c, the following results:



Further manipulation of the above equation can yield the second derivative of c with respect to S, commonly labelled Gamma or Γ.



The standardised normal probability distribution function and its derivative are of the following form:



Substituting the derivative of the normal probability distribution function into the second derivative of c with respect to S,

Click here to see skipped steps in this derivation


The third derivative of C with respect to S is not given a Greek symbol. Using the above result,

Click here to see skipped steps in this derivation


In summary,

The day started out an ordinary day: I woke up late, skipped breakfast and brisk-walked to work without coffee.

Work, as usual, was work.

As I was leaving the office, I read a text message from a little cousin of mine:
"I was offered n % of my company to become a partner."

The day immediately became better. A smile cracked across my face. Passers-by might have thought my daughter had just been awarded with a PhD in mathematical physics, but this is better- my cousin was offered a partnership.

This cousin of mine treated me to a gelato for my birthday. Asked me to buy myself a gelato, she’d pay me back later. "Get 3 scoops," she insisted, "then try not to shit on that day."
"WTF?"
"So my gelato no need to come out so fast. Hahahaha."

I know she will not take the partnership offer; she has grand plans to see more of the world before getting well and truly bogged down by work. Still, it’s not a matter of being a partner or not, it’s the fact that her talents have been acknowledged.

In celebration of this recognition, a dinner in Hong Kong on my behalf is in order.


Congratulations, little cousin. *raises wine glass bowl of mango sago*