Deriving the first partial derivatives of the Black-Scholes call price equation
Material presented here will be used to discuss hedging strategies to simultaneously hedge an options portfolio against various exposures.
The call option price:
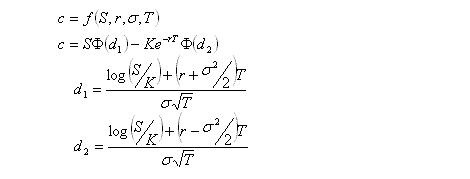
The partial derivatives of d1 and d2:
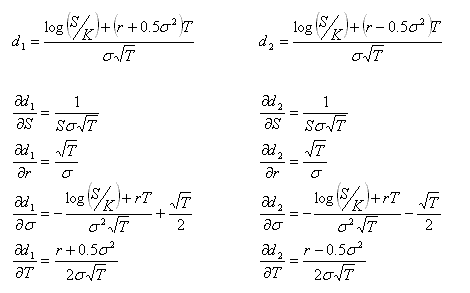
Partial differentiating c with respect to each variable:
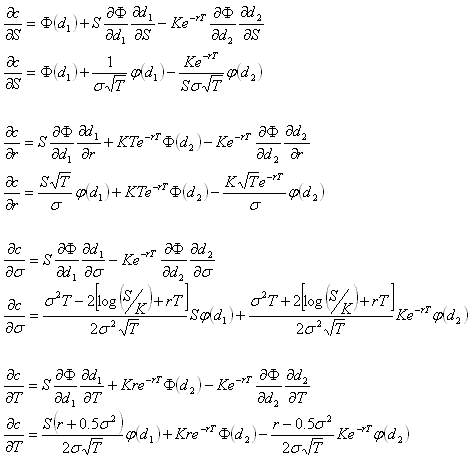
And we're done for today. Easy, no?
The call option price:
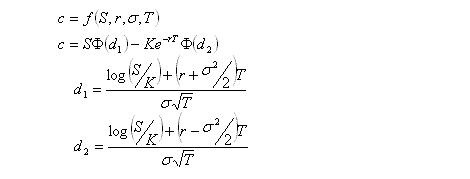
The partial derivatives of d1 and d2:
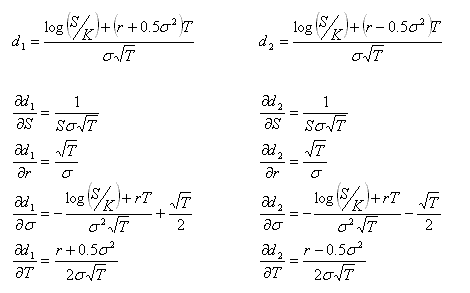
Partial differentiating c with respect to each variable:
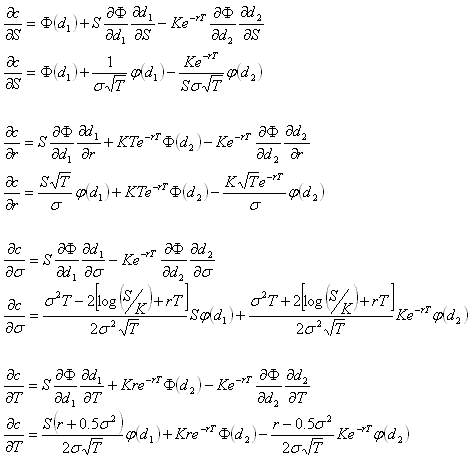
And we're done for today. Easy, no?
Labels: applied mathematics, finance, mathematics

<< Home