Deriving the exact equations for Delta, Gamma and the unnamed third price-derivative of a call option
An underlying knowledge of options is assumed. This post is intended to demonstrate various parameters that will be used in a future post.
Using the Black-Scholes model for options pricing, a call option price is:
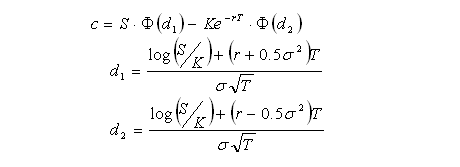
Where Φ(x) is the cumulative probability function of a standardised normal variable.
Using partial derivatives, the rate of change of c with respect to S will be derived. This rate of change is commonly labelled Δ, Delta.
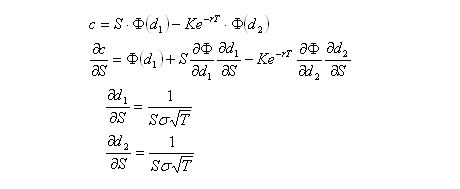
The normalised probability function and cumulative probability function are related in the following manner:
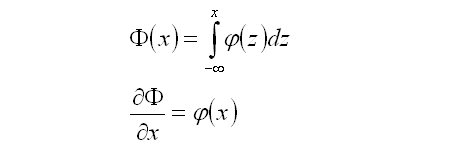
Substituting this into the partial derivative of c, the following results:
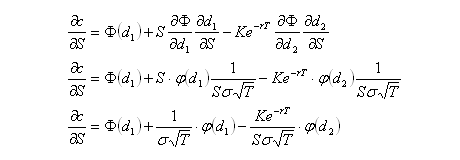
Further manipulation of the above equation can yield the second derivative of c with respect to S, commonly labelled Gamma or Γ.
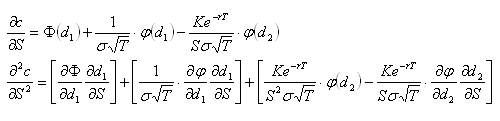
The standardised normal probability distribution function and its derivative are of the following form:
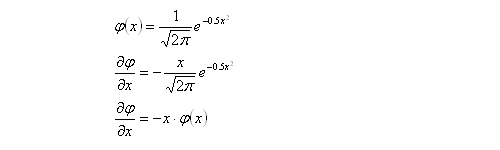
Substituting the derivative of the normal probability distribution function into the second derivative of c with respect to S,
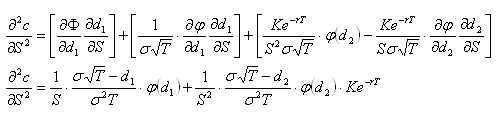
Click here to see skipped steps in this derivation
The third derivative of C with respect to S is not given a Greek symbol. Using the above result,

Click here to see skipped steps in this derivation
In summary,
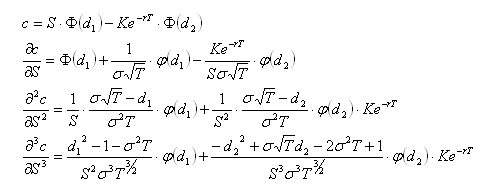
Using the Black-Scholes model for options pricing, a call option price is:
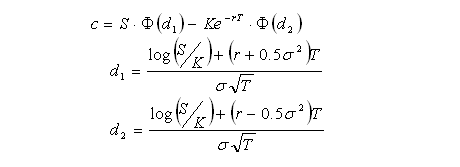
Where Φ(x) is the cumulative probability function of a standardised normal variable.
Using partial derivatives, the rate of change of c with respect to S will be derived. This rate of change is commonly labelled Δ, Delta.
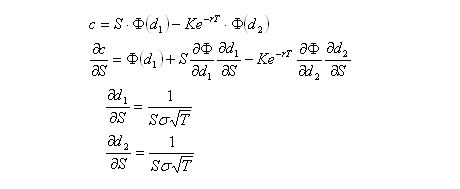
The normalised probability function and cumulative probability function are related in the following manner:
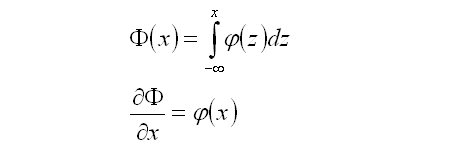
Substituting this into the partial derivative of c, the following results:
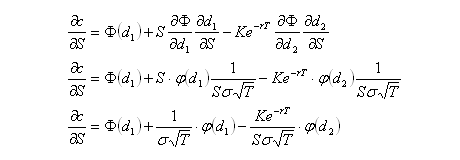
Further manipulation of the above equation can yield the second derivative of c with respect to S, commonly labelled Gamma or Γ.
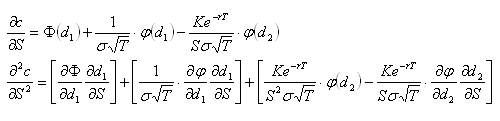
The standardised normal probability distribution function and its derivative are of the following form:
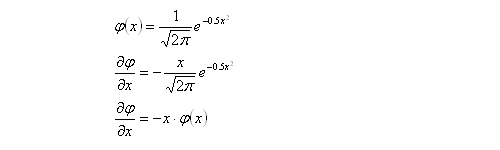
Substituting the derivative of the normal probability distribution function into the second derivative of c with respect to S,
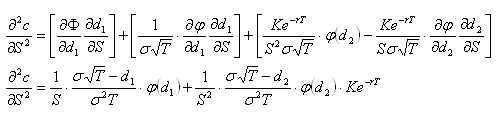
Click here to see skipped steps in this derivation
The third derivative of C with respect to S is not given a Greek symbol. Using the above result,

Click here to see skipped steps in this derivation
In summary,
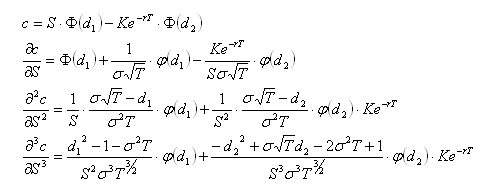
Labels: finance, mathematics

<< Home