Hydrodynamics for noobs
Seeing that my work load is particularly low today, I’ll attempt to clarify some fundamental concepts regarding the flow of water1 through pipes and fittings.
A very fundamental notion to understand in hydraulics is the relationship between flow speed and pressure. A partially blocked pipe will be used to illustrate this relationship.
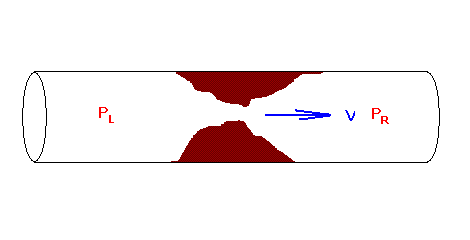
In this example, the pressure on the left, PL, is greater than the pressure on the right, PR. This pressure difference will accelerate water through the blockage, from left to right. As the speed of water flow increases, friction also increases. This friction force is proportional to the square of velocity: doubling the velocity results in four times the friction; tripling the velocity results in nine times the friction.
The flow of water will continue to increase until such a flow speed where the pressure difference, PL - PR is balanced by the friction of water rushing through the narrow blockage.
Instead of expressing the friction/ flow resistance as a friction force, it is commonly expressed as a pressure difference between the upstream and downstream areas, as a function of flow speed.
ΔP = kV2
This approach to expressing flow resistance is very convenient for practical problems. For example, one may wish to pump a certain volume of water through a valve into a water tank. If the desired flow speed V is known, and the valve’s value of k is known, the pressure difference between the valve’s front and back can be determined. Knowing the pressure inside the water tank, the pressure before the valve needs to be greater than the tank’s pressure by ΔP. This approach also can be used if there are several valves: the pressure difference across the valves can be added together to find out the total pressure loss that occurs when water flows through the system.
What happens when you open a valve in a water tap?
For simplicity, we will assume the water source for a tap is at a constant pressure, and the tap opens out to atmospheric pressure. This is quite a reasonable assumption, especially if the tap is connected directly to a water tank with very minimal lengths of piping.
As is the case for water taps, opening the valve allows water to flow out of the tap. Water flows from the high pressure side through the valve and out to the low pressure side. The flow speed is limited by the tap’s flow resistance k.
As shown above, the flow speed and pressure difference is related by ΔP = kV2. Given that the pressure difference does not change, the only way to regulate the quantity of water coming out of the tap is by changing k. This happens when the valve is opened or closed. When the valve is closed, k increases (completely closed, the value of k is infinity- there is zero flow even when pressure difference is a finite quantity). When the valve is opened, k decreases.
Notes:
1. or any other viscous and incompressible fluid
A very fundamental notion to understand in hydraulics is the relationship between flow speed and pressure. A partially blocked pipe will be used to illustrate this relationship.

In this example, the pressure on the left, PL, is greater than the pressure on the right, PR. This pressure difference will accelerate water through the blockage, from left to right. As the speed of water flow increases, friction also increases. This friction force is proportional to the square of velocity: doubling the velocity results in four times the friction; tripling the velocity results in nine times the friction.
The flow of water will continue to increase until such a flow speed where the pressure difference, PL - PR is balanced by the friction of water rushing through the narrow blockage.
Instead of expressing the friction/ flow resistance as a friction force, it is commonly expressed as a pressure difference between the upstream and downstream areas, as a function of flow speed.
ΔP = kV2
This approach to expressing flow resistance is very convenient for practical problems. For example, one may wish to pump a certain volume of water through a valve into a water tank. If the desired flow speed V is known, and the valve’s value of k is known, the pressure difference between the valve’s front and back can be determined. Knowing the pressure inside the water tank, the pressure before the valve needs to be greater than the tank’s pressure by ΔP. This approach also can be used if there are several valves: the pressure difference across the valves can be added together to find out the total pressure loss that occurs when water flows through the system.
What happens when you open a valve in a water tap?
For simplicity, we will assume the water source for a tap is at a constant pressure, and the tap opens out to atmospheric pressure. This is quite a reasonable assumption, especially if the tap is connected directly to a water tank with very minimal lengths of piping.
As is the case for water taps, opening the valve allows water to flow out of the tap. Water flows from the high pressure side through the valve and out to the low pressure side. The flow speed is limited by the tap’s flow resistance k.
As shown above, the flow speed and pressure difference is related by ΔP = kV2. Given that the pressure difference does not change, the only way to regulate the quantity of water coming out of the tap is by changing k. This happens when the valve is opened or closed. When the valve is closed, k increases (completely closed, the value of k is infinity- there is zero flow even when pressure difference is a finite quantity). When the valve is opened, k decreases.
Notes:
1. or any other viscous and incompressible fluid
Labels: applied science, physics

<< Home