Beauty in an ordered set plantation
When driving along large, well ordered plantations, one often notices that the trees appear to line up in straight lines when one looks in different directions. The simplest example will be using a square grid as follows:
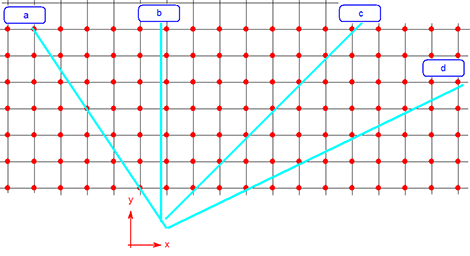
As the observer looks along the directions a, b, c, and d, he sees neat rows where tree trunks lined up. The directions a, b, c and d can start to make more sense when we express the gradient of the lines-of-sight:
We start with line d, for that is the simplest to explain:

This is derived by observing that y increases by one step when x increases by 2 steps. Similarly, the gradients for the other lines are:
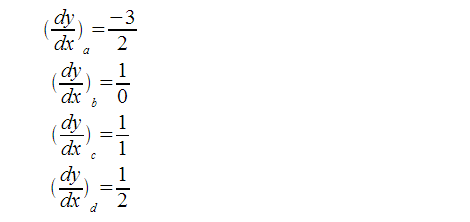
The above shows that lines of sights with integer numerators and integer denominators will have ordered rows of trees. However, it should be noted that 2/2 is equal to 1/1, thus some integer-pairs need to be eliminated. This can be done by dividing both the numerator and denominator by all their common factors. In other words, the numerator and denominator is to be relatively-prime.
At this point, the argument is starting to look remarkably similar to the well known problem of “how many rational numbers are there?” The answer is infinity.
Thus, in an infinitely large plantation with trees of infinitesimally narrow trunks (this is a necessary condition to prevent other trees' trunks from blocking the line of sight), there are infinitely many lines of sights that result in orderly lines. Of course, it is naturally assumed that in this odd plantation, the spacing and arrangement of trees are perfectly regular.
The strength of the visible trend line of lined-up trees depends on how far one needs to move along the line of sight before another tree is sighted. In other words, the visibility of the trend line is dependent on the linear density of the trees along the line of sight.
The packing density can be inferred by the numerator and denominator of the gradient (when already expessed as relatively-prime numbers). The separation distance of trees along the line of sight is simply the hypotenuses of the triangle consisting of the perpendicular sides of lengths [numerator] and [denominator]. The separation distance is thus:

Thus, for a line of sight to be a very obvious one, both x and y must be small to result in more trees occurring along the line of sight. This is consistent with general observations in the field that the line of trees along the line of sight b is more obvious than the line along c, which is more obvious than along d, which is more obvious than along a.
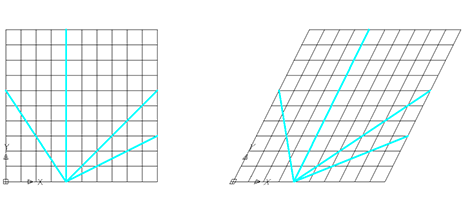
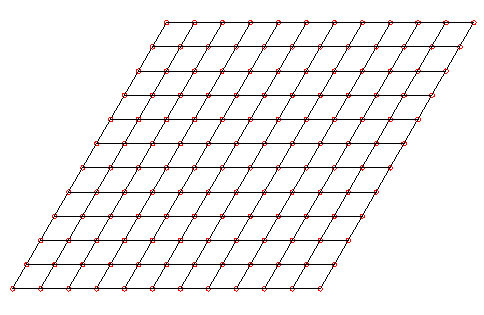
This approach to analysis can apply to non-orthogonal layouts as well. For example, if the grid was deformed as follows, the analysis above still applies.
However, inference of the strength of the trend line requires explicit coordinate manipulation to determine the exact inter-tree spacing (the equation of s=sqrt (x^2 + y^2) does not apply for non-orthogonal x and y).
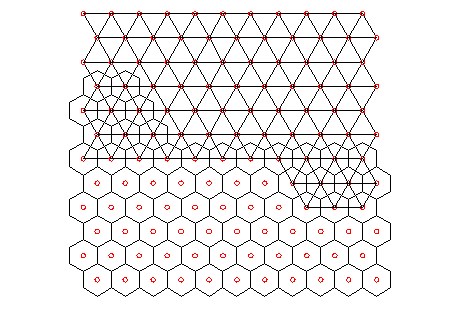
If the plantation was arrayed in a hexagonal/triangular layout (which allows the greatest packing density of trees), the above analysis can still be used. (note: in this arrangement, trees can be the vertices of the triangles, of the the centres of hexagons. This is illustrated below)
The hexagonal/triangular layout can be recast as a deformed square (properly called a parallelogram), as shown below:

As the observer looks along the directions a, b, c, and d, he sees neat rows where tree trunks lined up. The directions a, b, c and d can start to make more sense when we express the gradient of the lines-of-sight:
We start with line d, for that is the simplest to explain:

This is derived by observing that y increases by one step when x increases by 2 steps. Similarly, the gradients for the other lines are:
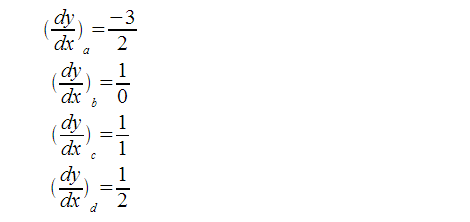
The above shows that lines of sights with integer numerators and integer denominators will have ordered rows of trees. However, it should be noted that 2/2 is equal to 1/1, thus some integer-pairs need to be eliminated. This can be done by dividing both the numerator and denominator by all their common factors. In other words, the numerator and denominator is to be relatively-prime.
At this point, the argument is starting to look remarkably similar to the well known problem of “how many rational numbers are there?” The answer is infinity.
Thus, in an infinitely large plantation with trees of infinitesimally narrow trunks (this is a necessary condition to prevent other trees' trunks from blocking the line of sight), there are infinitely many lines of sights that result in orderly lines. Of course, it is naturally assumed that in this odd plantation, the spacing and arrangement of trees are perfectly regular.
The strength of the visible trend line of lined-up trees depends on how far one needs to move along the line of sight before another tree is sighted. In other words, the visibility of the trend line is dependent on the linear density of the trees along the line of sight.
The packing density can be inferred by the numerator and denominator of the gradient (when already expessed as relatively-prime numbers). The separation distance of trees along the line of sight is simply the hypotenuses of the triangle consisting of the perpendicular sides of lengths [numerator] and [denominator]. The separation distance is thus:

Thus, for a line of sight to be a very obvious one, both x and y must be small to result in more trees occurring along the line of sight. This is consistent with general observations in the field that the line of trees along the line of sight b is more obvious than the line along c, which is more obvious than along d, which is more obvious than along a.
This approach to analysis can apply to non-orthogonal layouts as well. For example, if the grid was deformed as follows, the analysis above still applies.

However, inference of the strength of the trend line requires explicit coordinate manipulation to determine the exact inter-tree spacing (the equation of s=sqrt (x^2 + y^2) does not apply for non-orthogonal x and y).
If the plantation was arrayed in a hexagonal/triangular layout (which allows the greatest packing density of trees), the above analysis can still be used. (note: in this arrangement, trees can be the vertices of the triangles, of the the centres of hexagons. This is illustrated below)

The hexagonal/triangular layout can be recast as a deformed square (properly called a parallelogram), as shown below:

Labels: applied mathematics, mathematics

<< Home