An interesting difference between the human eye and a still camera
Warning: Slipshod handwaving arguments ahead. Rigorous people proceed with care.
There are many comparisons that draw attention to the similarities between the human eye and a still camera. Today, I will point out one interesting but rarely, if ever, mentioned difference.
In the human eye, the signal strength can be assumed to be approximately proportional to the quantity of light falling on the retinal cells.
Simplistically,
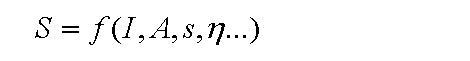
Where the signal strength coming out of the eye is a function of light intensity falling on the retina, aperture of the pupil, retina sensitivity, efficiency and other eye-related parameters.
In a still camera, there is one more parameter that dramatically changes the form of the equation- the exposure time.
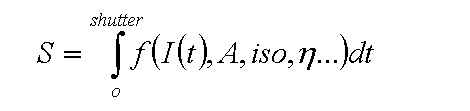
Here, the fact that light intensity that falls on the sensor can vary with time is highlighted, hence it is not a constant but denoted by a time-dependent function I(t). Aperture, sensor sensitivity (ISO), light transmission efficiency and other camera-related parameters are assumed to be fixed for each exposure.
And, the signal strength is the time integral of the function. Which sort of makes sense, since doubling the exposure time in the presence of a constant light source results in photographs twice as bright.
It is exactly this time integral that allows double exposures to be made, where the film is exposed to two different scenes to create an overlapping image.
If the exposures were made 24 hours apart, then the integral can be taken to be starting from 0 and ending 24 hours later, with I(t) being zero for a large proportion of the time (since the film was not exposed to light between exposures).
Mathematics
There are many comparisons that draw attention to the similarities between the human eye and a still camera. Today, I will point out one interesting but rarely, if ever, mentioned difference.
In the human eye, the signal strength can be assumed to be approximately proportional to the quantity of light falling on the retinal cells.
Simplistically,
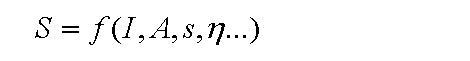
Where the signal strength coming out of the eye is a function of light intensity falling on the retina, aperture of the pupil, retina sensitivity, efficiency and other eye-related parameters.
In a still camera, there is one more parameter that dramatically changes the form of the equation- the exposure time.
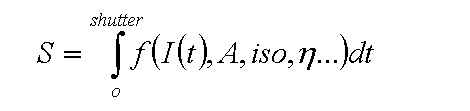
Here, the fact that light intensity that falls on the sensor can vary with time is highlighted, hence it is not a constant but denoted by a time-dependent function I(t). Aperture, sensor sensitivity (ISO), light transmission efficiency and other camera-related parameters are assumed to be fixed for each exposure.
And, the signal strength is the time integral of the function. Which sort of makes sense, since doubling the exposure time in the presence of a constant light source results in photographs twice as bright.
It is exactly this time integral that allows double exposures to be made, where the film is exposed to two different scenes to create an overlapping image.
If the exposures were made 24 hours apart, then the integral can be taken to be starting from 0 and ending 24 hours later, with I(t) being zero for a large proportion of the time (since the film was not exposed to light between exposures).
Mathematics
Labels: mathematics, natural science, photography

<< Home