Dimensional Analysis and unit conversion methods
Dimensional analysis
One of the tools I found in my secondary school years was dimensional analysis, although I did not know its name back then. The technique is so powerful yet simple, in hindsight, I’m surprised it was not taught in school.
The basic premise of dimensional analysis lies in the fact that units cannot be magically converted from a metre to a Volt. Units (be it metre, Volt, Francs, mole, Ampere, or Lumens) can be treated as algebriac variables and manipulated along with the numbers. Consider the much memorised equation, the equation relating displacement s, acceleration a, initial velocity u and time elapsed t.
Commonly, it is expressed as such:

If we were to consider the units of each variable, using SI units:
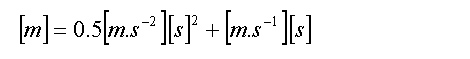
The time units [seconds] cancel each other completely, and the entire equation is expressed in metres, which is a good sign:
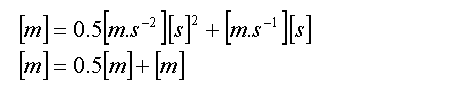
If upon writing out an equation, and performing a quick dimensional analysis it does not balance, say, Joules equal to seconds, then there is a missing term somewhere in the equation. Either that, or you need to improve on your dimensional analysis skills.
Here is an example question just to illustrate dimensional analysis:
The challenge is figuring out which terms are required in the calculation, and how to use these equations in the calculation.
So we need to find out the duration, measured in seconds (usually). We start with the first dimension, time, and fill in variables (either by division or multiplication) such that unwanted dimensions cancel each other, and wanted dimensions are preserved. Evidently, we must do it such that time = time, not time = energy nor time = money.
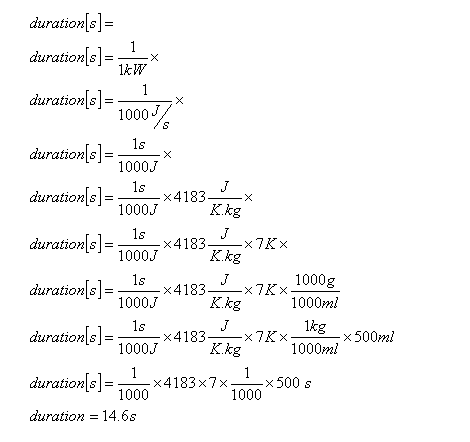
Note that we do not even have to consider the surface tension, since the units do not come into the picture.
Simple isn’t it?
Unit conversion
Several days ago, a friend (final year mechanical engineering student, for your information) asked me how to convert from rpm (revs/minute) to rad/s (radians per second). I was appalled.
Say we have an engine, from a Honda Civic Tyre R, incidentally. It rotates at 8000 rpm. What’s the angular speed in radians/second?

Another example: the density of water is 998.2 kg per cubic metre. What’s the density in pounds per cubic foot?
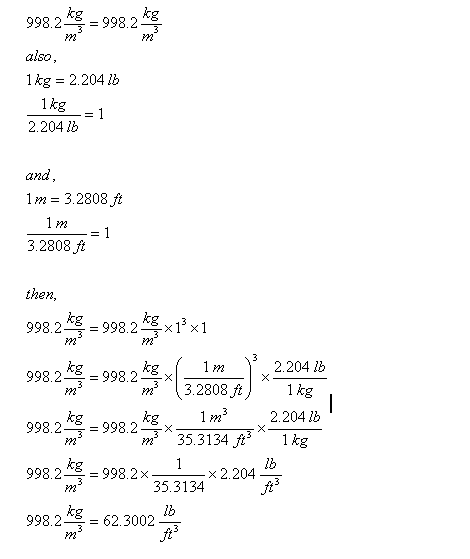
Note that the conversion factor between metres and feet has to be cubed, since the units are cubic distances. After all, a cube of sides length 1 metre has volume 1 cubic metre, and this cube has sides of lengths 3.2808 feet sides, which gives a volume of 3.2808 ^3 = 35.3134 cubic ft.
You’re welcome.
Mathematics & applied science
One of the tools I found in my secondary school years was dimensional analysis, although I did not know its name back then. The technique is so powerful yet simple, in hindsight, I’m surprised it was not taught in school.
The basic premise of dimensional analysis lies in the fact that units cannot be magically converted from a metre to a Volt. Units (be it metre, Volt, Francs, mole, Ampere, or Lumens) can be treated as algebriac variables and manipulated along with the numbers. Consider the much memorised equation, the equation relating displacement s, acceleration a, initial velocity u and time elapsed t.
Commonly, it is expressed as such:

If we were to consider the units of each variable, using SI units:
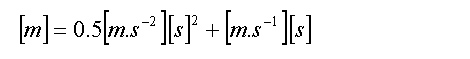
The time units [seconds] cancel each other completely, and the entire equation is expressed in metres, which is a good sign:
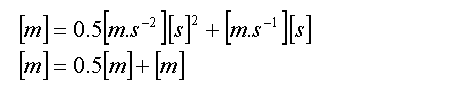
If upon writing out an equation, and performing a quick dimensional analysis it does not balance, say, Joules equal to seconds, then there is a missing term somewhere in the equation. Either that, or you need to improve on your dimensional analysis skills.
Here is an example question just to illustrate dimensional analysis:
500ml of water is heated in an insulated beaker using an electric heater rated at 1kW. How long does it take to raise the water temperature by 7 Kelvins?
Given that the specific volume of water is 1 ml/g, the specific heat capacity of water is 4183 J/K.kg, surface tension of 72.8 dynes/cm.
The challenge is figuring out which terms are required in the calculation, and how to use these equations in the calculation.
So we need to find out the duration, measured in seconds (usually). We start with the first dimension, time, and fill in variables (either by division or multiplication) such that unwanted dimensions cancel each other, and wanted dimensions are preserved. Evidently, we must do it such that time = time, not time = energy nor time = money.
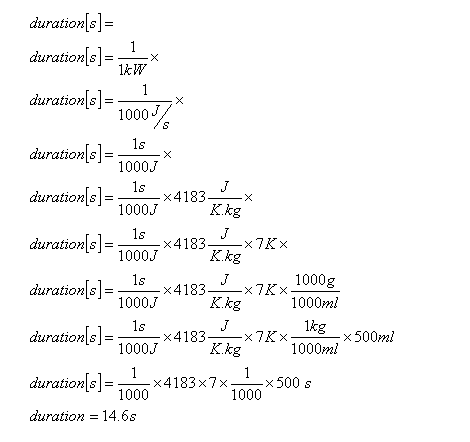
Note that we do not even have to consider the surface tension, since the units do not come into the picture.
Simple isn’t it?
Unit conversion
Several days ago, a friend (final year mechanical engineering student, for your information) asked me how to convert from rpm (revs/minute) to rad/s (radians per second). I was appalled.
Say we have an engine, from a Honda Civic Tyre R, incidentally. It rotates at 8000 rpm. What’s the angular speed in radians/second?

Another example: the density of water is 998.2 kg per cubic metre. What’s the density in pounds per cubic foot?
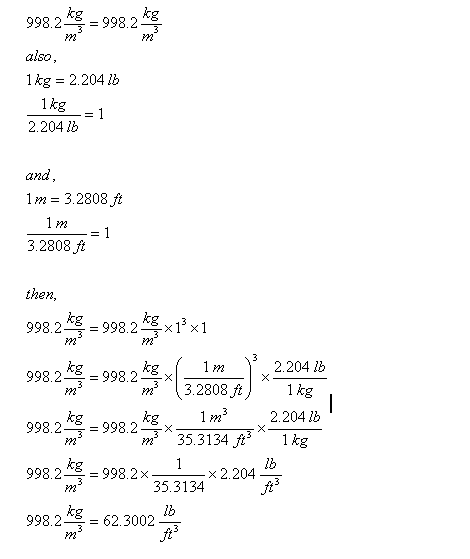
Note that the conversion factor between metres and feet has to be cubed, since the units are cubic distances. After all, a cube of sides length 1 metre has volume 1 cubic metre, and this cube has sides of lengths 3.2808 feet sides, which gives a volume of 3.2808 ^3 = 35.3134 cubic ft.
You’re welcome.
Mathematics & applied science
Labels: applied mathematics

<< Home