I'll stop writing in Chinese for the time being
English translation and more below.
我想我暂时不会努力写中文文章了。目前,重要的是把词汇学大,对语法熟悉。写作在这两方面是无法协助的,要多阅读、翻词典才行。
在过去了的几个星期,发觉自己有很不错的进步。开始时,许多简单常用的词都认不出,例如:无聊、获得、埋葬、虚心等。现在,读新闻报告时虽然不是每个词都明,但是文章所传达的我看得懂。
在阅读的过程中,也对亲戚朋友名字的意思了解了一些。
知识渊博的科学家。
鼎鼎大名的大臣。
姿态如君的校友。
妖媚的表妹。
英俊的弟弟。
人才光耀的校友。
打球优越的黑人。
八打灵的圣贤。
杰出的同窗。
善良的总统。
***
For the time being, I’ll be less diligent in my Chinese writing. At the moment, the most important aspect of my education is to vastly improve my vocabulary and be familiar with the grammar and sentence structures. To this end, I will be reading and looking up the dictionary; writing is of no help now.
I feel I’ve made decent progress over the past weeks. When I started I had trouble recognising simple characters like … I’ll not embarrass myself by publishing that sample list here. I can now read news articles, although not to absolute comprehension.
***
On a separate note, I’ve unexpectedly got 2 very interesting questions on my hands, one geometry, the other higher arithmetic.
The higher arithmetic one is particularly fascinating (because it can be written succinctly):
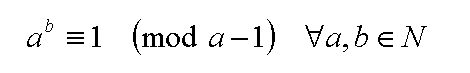
a raised to the power of b is congruent to 1 modulo (a-1) for all a and b that are natural numbers
It’s a generalised statement on one of the key arguments used in solving the JFE8555 problem. Previously, it had never been rigorously proven in solving that problem, although the numerical examples gave (me) ample confidence in the equation.
It’s a two parameter problem, so proof by induction is not likely to work. It’s going to be difficult.
Personal
我想我暂时不会努力写中文文章了。目前,重要的是把词汇学大,对语法熟悉。写作在这两方面是无法协助的,要多阅读、翻词典才行。
在过去了的几个星期,发觉自己有很不错的进步。开始时,许多简单常用的词都认不出,例如:无聊、获得、埋葬、虚心等。现在,读新闻报告时虽然不是每个词都明,但是文章所传达的我看得懂。
在阅读的过程中,也对亲戚朋友名字的意思了解了一些。
知识渊博的科学家。
鼎鼎大名的大臣。
姿态如君的校友。
妖媚的表妹。
英俊的弟弟。
人才光耀的校友。
打球优越的黑人。
八打灵的圣贤。
杰出的同窗。
善良的总统。
For the time being, I’ll be less diligent in my Chinese writing. At the moment, the most important aspect of my education is to vastly improve my vocabulary and be familiar with the grammar and sentence structures. To this end, I will be reading and looking up the dictionary; writing is of no help now.
I feel I’ve made decent progress over the past weeks. When I started I had trouble recognising simple characters like … I’ll not embarrass myself by publishing that sample list here. I can now read news articles, although not to absolute comprehension.
On a separate note, I’ve unexpectedly got 2 very interesting questions on my hands, one geometry, the other higher arithmetic.
The higher arithmetic one is particularly fascinating (because it can be written succinctly):
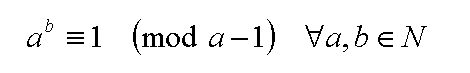
a raised to the power of b is congruent to 1 modulo (a-1) for all a and b that are natural numbers
It’s a generalised statement on one of the key arguments used in solving the JFE8555 problem. Previously, it had never been rigorously proven in solving that problem, although the numerical examples gave (me) ample confidence in the equation.
It’s a two parameter problem, so proof by induction is not likely to work. It’s going to be difficult.
Personal
Labels: chinese posts, personal

<< Home