Geometric proof of Pythagoras’ Theorem

Squaring the triangle

[The illustrations' colours are a bit messed up in the BMP to JPG file conversion. Just squint and hope you can discern the black from the blue. If you can't, it is no problem anyway.]

The ancient Greeks did it with whatever tools they had. I’m repeating it with AutoCAD 2006 as an illustration aid.

Pythagoras’ Theorem states that for any right-angle triangle with side lengths a, b and c, such that c is the length of the hypogenous,

a^2 + b^2 = c^2

Start with a right-angle triangle, with the hypogenous (the longest line) coloured red as illustrated in Figure 1.


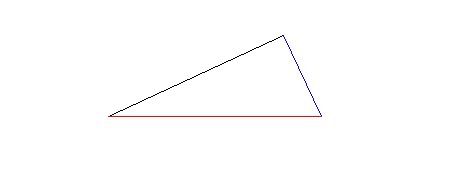
Figure 1


Attach squares to each side of the triangle (Figure 2). If Pythagoras was right, the area of the red square is equal to the sum of the area of the black and blue squares.


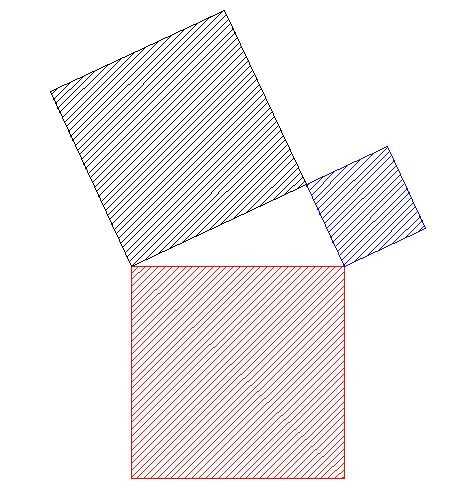
Figure 2


All subsequent operations will be purely shifting, dividing and rotating (by 90 degrees) areas.

Shift the red square upwards as shown in Figure 3.


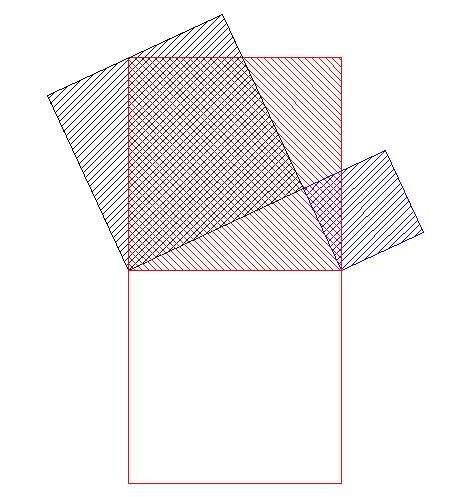
Figure 3


The black triangle protruding out from the left of the red square is equivalent to the original right-angle triangle since all lengths are the same (squares have sides of equal length). This triangle can then be rotated into the space where the original triangle is located, as performed in Figure 4.


Figure 4


The blue square is shifted upwards to upper black triangle, Figure 5.


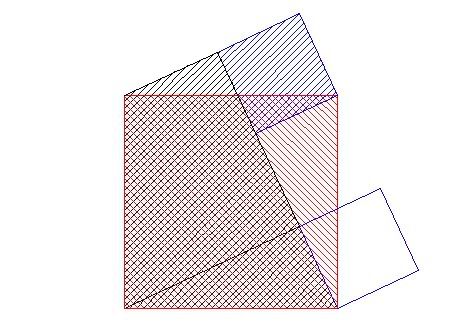
Figure 5


The blue and black triangle above the red square can then be rotated to fit into the empty area in the left portion of the red square (Figure 6).


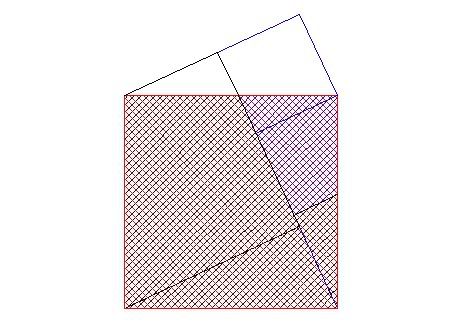
Figure 6


The areas are shown to be equivalent, and Pythagoras is correct in his theorem (Figure 7).


Figure 7




Mathematics