A brief introduction to tidal forces

For me, the tides have been slightly troubling for as long as I can remember.

The most disturbing question was, why does high tide occurs on both sides of the earth in an elliptical shape, and not only the moon facing side?

The question was partially answered when I came across one of the last few chapters in 'Gravity: an introduction to Einstein’s general relativity'.


Consider a large array of small objects (mangoes, for example) freely falling towards a massive object (such as a star). Note that the separation of the individual mangoes is sufficiently large that the gravitational force and direction is not the same for all the mangoes.



At a particular time, the mangoes are arranged in a circular fashion with one of them in the middle as shown. The gravitational force vectors acting on the individual mangoes are also illustrated as arrows indicating the direction and magnitude.



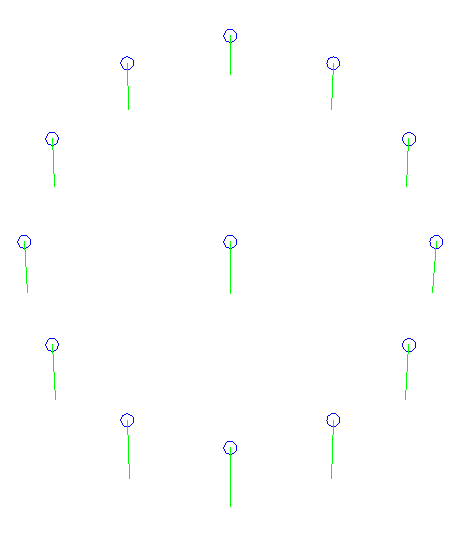
As expected for gravitation, the relationship is proportional to the inverse of the square of distance. Thus, a greater force is exerted on mangoes nearer to the star than mangoes further away.

All the mangoes are accelerating towards the star. However, mangoes closer to the star experience a greater gravitational attraction towards the star, and thus accelerate faster towards the star. Similarly, mangoes further away accelerate slower. The end result is that the mangoes fall at different rates, and the circular array starts to deform. The circle stretches into an ellipse.



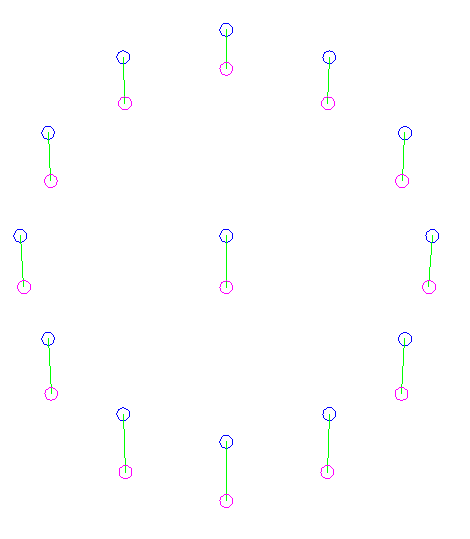
Apart from the forces’ magnitude, there is also a difference in force directions. The mangoes are all falling towards the centre of the star, but the mangoes are so far apart that they do not fall in parallel paths.

As a result of this converging nature of the free fall paths, the circle also narrows. The illustration shows the mangoes’ position at an interval after the time when they were arranged in the circular layout.

And thus the elliptical shape of the ocean’s tides has partly been explained. A more complete explanation will require that the moon and earth are orbiting each other as opposed to the radial plunge illustrated here using falling mangoes.


Blue curve: circle
Magenta curve: ellipse

Note that the force difference due to the moon is not particularly large; it causes a change in water level of only several metres, considering that the diameter of the earth is 12000 kilometres.

If an unfortunate person were to fall into a smallish black hole, the tidal forces near the singularity would be sufficient to tear the person apart. Parts nearer to the black hole accelerate dramatically faster than parts further away, the difference being sufficient to break the person into pieces.


Method for producing images:

AutoCAD was used to generate the images.
The circular array of mangoes has a radius of 4 units.
The distance between the centre of the array and the star is 60 units.
The distances between individual mangoes and the star were measured using the dimensioning tool
Gravitational attraction is proportional to the inverse of the square, thus this can be calculated from the measured distance.
For convenience, this gravitational force vector’s length was scaled arbitrarily such that the vector of force acting on the centre mango is 1 unit long.
Having determined the vector’s length on each mango, the vectors were drawn using the line tool.
The lines starts at the centre of each mango, and is pointed exactly at the centre of the star, and the line’s length adjusted accordingly.
The displaced positions of the mangoes are arbitrarily placed at the ends of the vector lines. This is acceptable for small time intervals (sufficiently small to neglect changes in gravitational force as the individual mango moves), since displacement s = 0.5at^t, and the displacements are all proportional to the vector lengths.
The final positions of the mangoes are exact, since they are derived as above.
The elliptical trend line is not an exact solution.


Mathematics, Physics