Finding the value of e
Euler’s number, e, is special in many ways. The exponential function of e is particularly fascinating in that the slope of the function at any point is equal to the function value at the point.
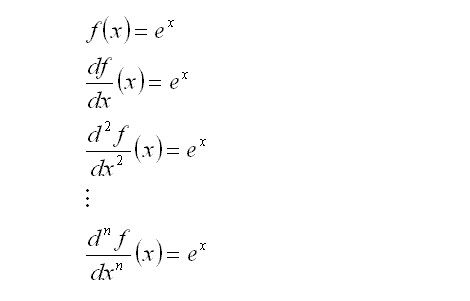
Since this is an exponential function, it should be reasonably easy to see that
f (0) = 1
f (1) = e
But what is the value of e?
Assuming the truth of the Taylor Series expansion of a function:
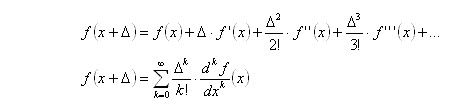
If we were to substitute the exponential function into the Taylor series, and let x = 0 and Δ = 1, then:
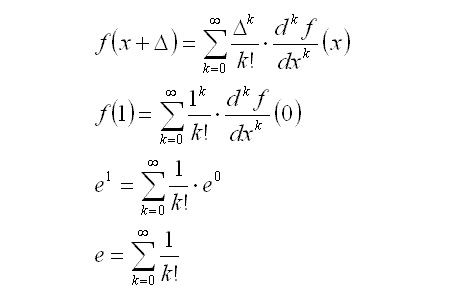
And there it is! The value of e is the sum of all the inverses of factorials. Expanding the summation:

Mathematics
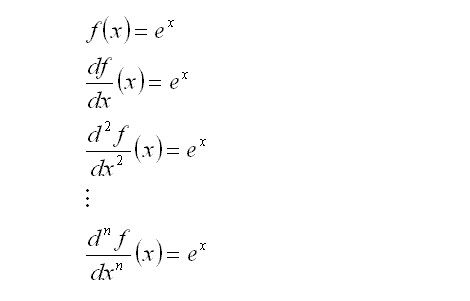
Since this is an exponential function, it should be reasonably easy to see that
f (0) = 1
f (1) = e
But what is the value of e?
Assuming the truth of the Taylor Series expansion of a function:
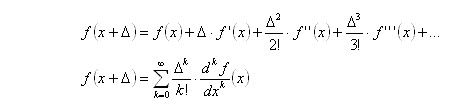
If we were to substitute the exponential function into the Taylor series, and let x = 0 and Δ = 1, then:
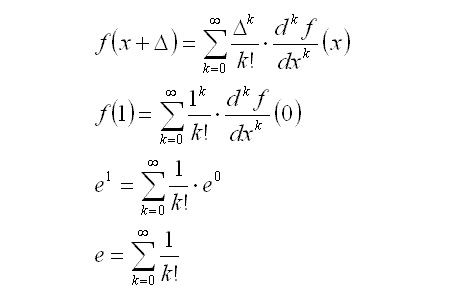
And there it is! The value of e is the sum of all the inverses of factorials. Expanding the summation:

Mathematics
Labels: mathematics, real numbers

<< Home