Night panoramic photography in Melbourne; complex number magic
This is going to be a mass of photographs, and tiny bit of mathematics.
On Thursday, Diana mentioned that Docklands is a promising venue for night photography. Said the bridge in that vicinity is beautiful. So I took a walk.
This is the aforementioned bridge.

Click here for large size image.
I then walked out on the old pier towards the central supports of the bridge. It was a long walk.

This was on one of the bridge's support columns, above deck level, shot with full telephoto on a tripod.

Click here for large size image.
The view back to where I snapped the first photo.

Click here for large size image.
I have no idea what this structure is, but it appears to be part of the old port’s infrastructure.
Note the new port across the harbour.

Click here for large size image
Parts of the pier were removed, leaving the supports exposed. Suitably sized condomettes were capped over the columns, presumably to prevent idiots from dancing on them. Also to prevent rainwater from stagnating at the top of the columns and rotting through the structures.

Huge cranes used to roll majestically over these tracks, presumably.

Docklands Panorama
Click here for large size image.
A 7-frame panoramic image spanning 90 degrees (horizontally). Measuring 3330 x 600 pixels and weighing 196 KB, it is large. Be patient, and remember to scroll sideways.

Water Feature
Click here for large size image.
Bali memorial, Melbourne.
And now, the mathematics:
Assumed knowledge: elementary knowledge of complex number manipulation
I always had trouble remembering the trigonometric identities for sin(a + b) and cos(a + b). Fret no more, Roger Penrose has pointed out a very nifty derivation using complex numbers.
Using the modulus and argument (some engineers may say magnitude and phase) notation, a complex number can be written as such:
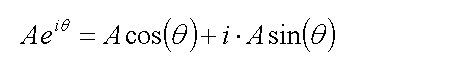
To obtain the trigonometric identities, expand the following complex number using the above expression.
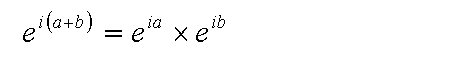
Do it, and be awed.
Photographs
Mathematics & Applied Sciences
On Thursday, Diana mentioned that Docklands is a promising venue for night photography. Said the bridge in that vicinity is beautiful. So I took a walk.
This is the aforementioned bridge.

Click here for large size image.
I then walked out on the old pier towards the central supports of the bridge. It was a long walk.

This was on one of the bridge's support columns, above deck level, shot with full telephoto on a tripod.

Click here for large size image.
The view back to where I snapped the first photo.

Click here for large size image.
I have no idea what this structure is, but it appears to be part of the old port’s infrastructure.
Note the new port across the harbour.

Click here for large size image
Parts of the pier were removed, leaving the supports exposed. Suitably sized condomettes were capped over the columns, presumably to prevent idiots from dancing on them. Also to prevent rainwater from stagnating at the top of the columns and rotting through the structures.

Huge cranes used to roll majestically over these tracks, presumably.

Docklands Panorama
Click here for large size image.
A 7-frame panoramic image spanning 90 degrees (horizontally). Measuring 3330 x 600 pixels and weighing 196 KB, it is large. Be patient, and remember to scroll sideways.

Water Feature
Click here for large size image.
Bali memorial, Melbourne.
And now, the mathematics:
Assumed knowledge: elementary knowledge of complex number manipulation
I always had trouble remembering the trigonometric identities for sin(a + b) and cos(a + b). Fret no more, Roger Penrose has pointed out a very nifty derivation using complex numbers.
Using the modulus and argument (
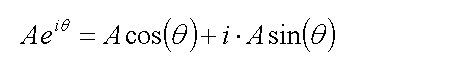
To obtain the trigonometric identities, expand the following complex number using the above expression.
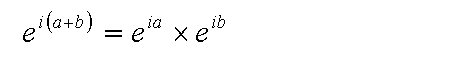
Do it, and be awed.
Photographs
Mathematics & Applied Sciences
Labels: mathematics, Melbourne, photography

<< Home