A brief explanation of the Taylor Series via the Mean Value Theorem
Assumed knowledge: some tertiary level calculus
Introduction
This article will explain the Taylor series by using the mean value theorem. The mean value theorem will be explained in a general manner before the proceeding on to the Taylor series.
The Taylor series will not be rigorously derived.
The mean-value theorem
For any continuous and differentiable function in the interval (x1,x2), there exists at least one point between x1 and x2 such that
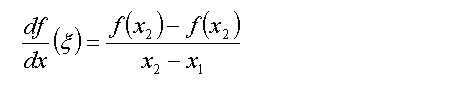
equation (1)
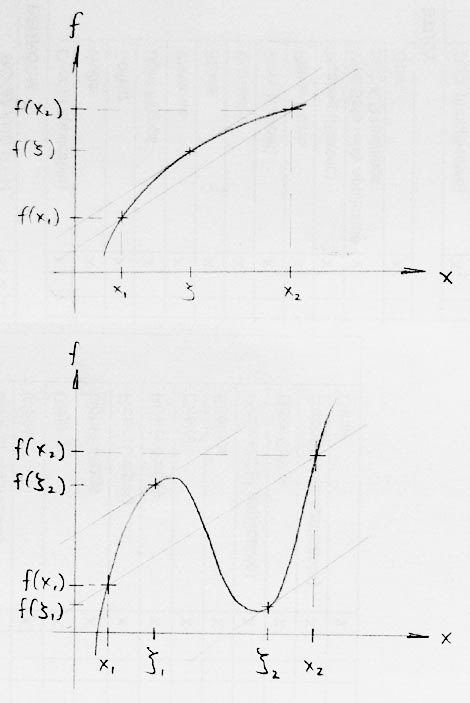
In other words, there is at least a point on the function between the two points that has slope equal to the slope between the two points x1 and x2.
2 graphs illustrate the point. Note the parallel lines.
While the mean value theorem may appear intimidating at first, it is conceptually identical to the idea presented below.
For a continuous function f, there exist a point ξ between x1 and x2 such that f(ξ) is the average of f(x1) and f(x2)
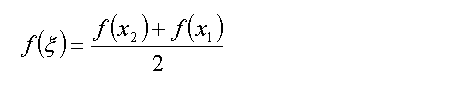
equation (2)

f(x1) and f(x2) are on different sides of the average f(ξ), and since the connection between f(x1) and f(x2) is continuous, this imples that there MUST be a point where the line crosses the average value.
The Taylor Series
The Taylor series is an expansion of a function about a point.
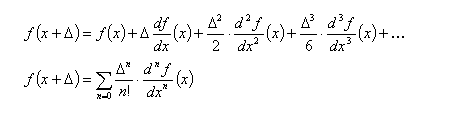
equation (3)
Using the mean value theorem, we can say that there exists a point ξ(1) between x and x+Δ that has slope equal to the slope of the line between the function values of x and x+Δ.
The expression of f(x+Δ) can then be written as follows:
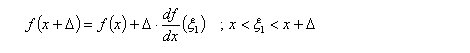
equation (4)
Again, note that the slope at ξ(1) is equal to the slope between the function values of x and x+Δ.
Now, for the most exciting part of this expansion. We will apply the mean value theorem onto the derivative in equation (4).
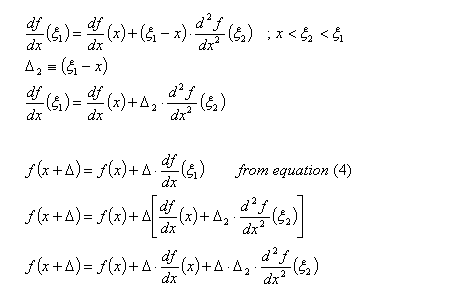
equation (5)
Repeating the above step for the second derivative:
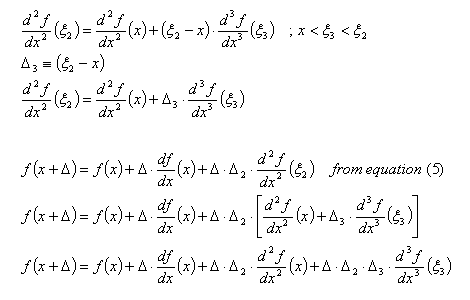
equation (6)
This step can be applied indefinitely onto higher and higher derivatives, and the result would be as follows:

equation (7)
For equation 7 to be equal to equation 3, the following would be true:

equation (8)
Unfortunately, equation 8 is not as easy to derive/proof as its simplicity may otherwise suggest. As such, this article would end here.
Mathematics
Introduction
This article will explain the Taylor series by using the mean value theorem. The mean value theorem will be explained in a general manner before the proceeding on to the Taylor series.
The Taylor series will not be rigorously derived.
The mean-value theorem
For any continuous and differentiable function in the interval (x1,x2), there exists at least one point between x1 and x2 such that
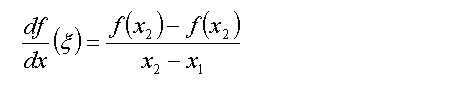
equation (1)
In other words, there is at least a point on the function between the two points that has slope equal to the slope between the two points x1 and x2.
2 graphs illustrate the point. Note the parallel lines.

While the mean value theorem may appear intimidating at first, it is conceptually identical to the idea presented below.
For a continuous function f, there exist a point ξ between x1 and x2 such that f(ξ) is the average of f(x1) and f(x2)
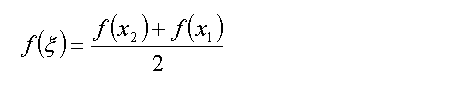
equation (2)

f(x1) and f(x2) are on different sides of the average f(ξ), and since the connection between f(x1) and f(x2) is continuous, this imples that there MUST be a point where the line crosses the average value.
The Taylor Series
The Taylor series is an expansion of a function about a point.
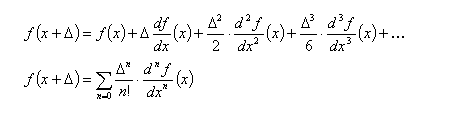
equation (3)
Using the mean value theorem, we can say that there exists a point ξ(1) between x and x+Δ that has slope equal to the slope of the line between the function values of x and x+Δ.
The expression of f(x+Δ) can then be written as follows:
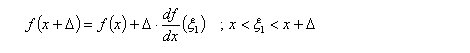
equation (4)
Again, note that the slope at ξ(1) is equal to the slope between the function values of x and x+Δ.
Now, for the most exciting part of this expansion. We will apply the mean value theorem onto the derivative in equation (4).
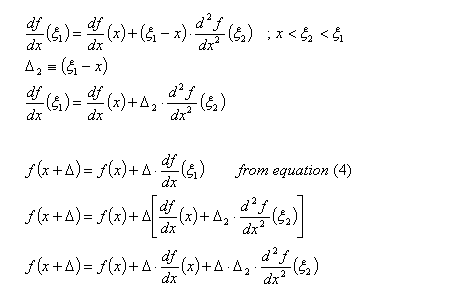
equation (5)
Repeating the above step for the second derivative:
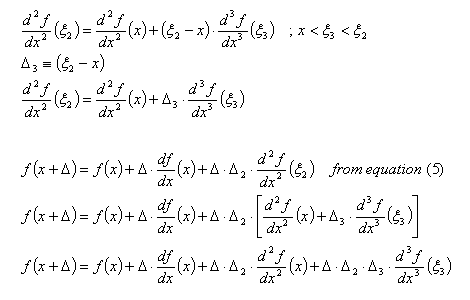
equation (6)
This step can be applied indefinitely onto higher and higher derivatives, and the result would be as follows:

equation (7)
For equation 7 to be equal to equation 3, the following would be true:

equation (8)
Unfortunately, equation 8 is not as easy to derive/proof as its simplicity may otherwise suggest. As such, this article would end here.
Mathematics
Labels: mathematics, real numbers

<< Home