Deriving the present value of a fixed-payment annuity of finite life (not a perpetuity)
Many finance text books will provide the formula for the present value of such an annuity as the following:

Where C is the payment made every period, r is the discount rate to be applied, and n is the number of periods.
Unfortunately, elementary finance text books have a distasteful habit of presenting equations with no proof. The reader can either believe it, or sod it.
Here, we will derive the above equation.
The present value of an annuity is the sum of the discounted payments, as follows.
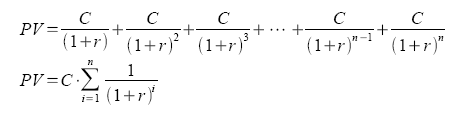
This sum can be expressed as the difference between two infinite sums (perpetuities) starting at different times:
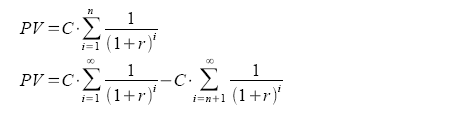
Notice that the second perpetuity starts at n+1. We then modify the second perpetuity's notation so that the index starts from 1:
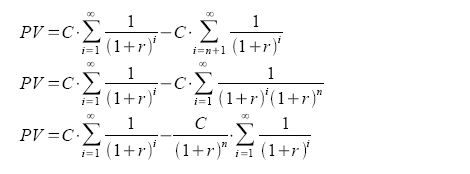
From studies of the present value of perpetuities, we know that the following is true:

Substituting the above equation into our present value of an annuity:
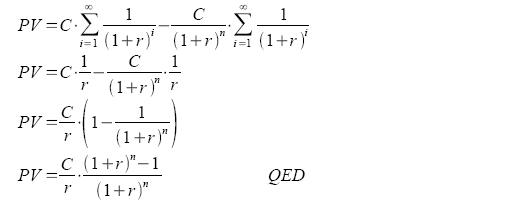
Appendix – deriving the present value of a perpetuity
A perpetuity is an endless stream of fixed payments occurring at fixed intervals.
Its present value can be computed as follows:
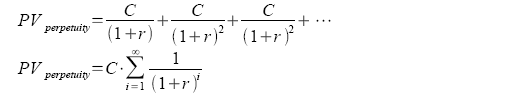
The value of the infinite sum can be expressed as follows:
For simplicity, 1+r is replaced with x.
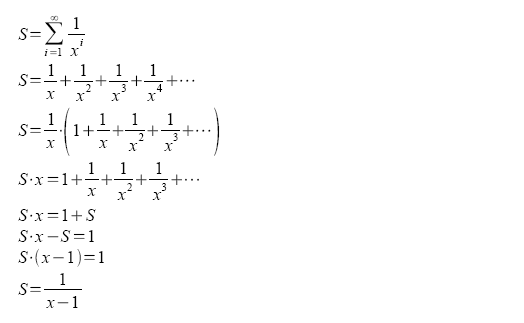
When we replace x back with 1+r, the equation becomes

Substituting our result into the present value of a perpetuity:


Where C is the payment made every period, r is the discount rate to be applied, and n is the number of periods.
Unfortunately, elementary finance text books have a distasteful habit of presenting equations with no proof. The reader can either believe it, or sod it.
Here, we will derive the above equation.
The present value of an annuity is the sum of the discounted payments, as follows.
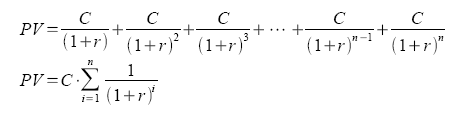
This sum can be expressed as the difference between two infinite sums (perpetuities) starting at different times:
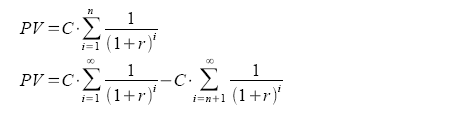
Notice that the second perpetuity starts at n+1. We then modify the second perpetuity's notation so that the index starts from 1:
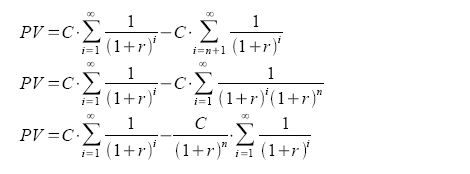
From studies of the present value of perpetuities, we know that the following is true:

Substituting the above equation into our present value of an annuity:
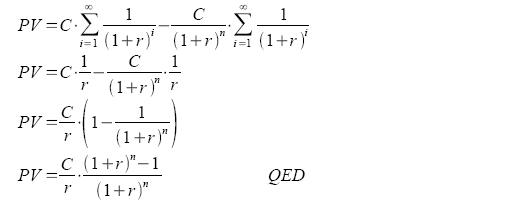
Appendix – deriving the present value of a perpetuity
A perpetuity is an endless stream of fixed payments occurring at fixed intervals.
Its present value can be computed as follows:
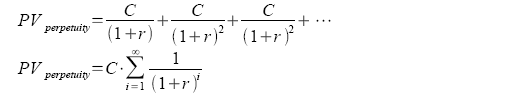
The value of the infinite sum can be expressed as follows:
For simplicity, 1+r is replaced with x.
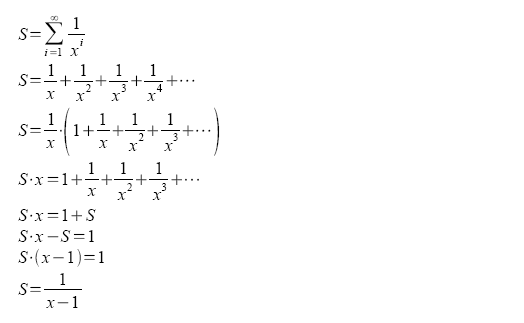
When we replace x back with 1+r, the equation becomes

Substituting our result into the present value of a perpetuity:

Labels: finance, mathematics

<< Home