Deriving the lower bound of option prices without explicit invocation of the no-arbitrage argument
The method of derivation presented here takes advantage of (in)equality of value rather than assuming no-arbitrage
Price of a call option, c
Price of a put option, p
Strike price of option, K
Time to expiry, T
Current market price of underlying commodity, S
Risk-free continuously compounded interest rate, r
On the expiry date, someone who holds a call option and some cash equal to the strike price (K) can choose to buy the commodity at the fixed price K regardless of the market price (S) of the commodity. Obviously, if the market price turns out to be higher than the strike price, the buyer gets to buy at a lower price, which means the option is now worth a bundle of money. On the other hand, if the strike price is higher than market price, the holder will not exercise the option and the option is worth nothing.
Therefore, it follows that the call option plus K in cash is at least as valuable as the commodity’s market price (S). On the expiry date, the value of a call option obeys the following correlation:
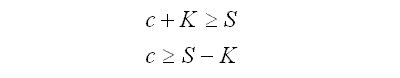
If it is not yet the expiry date, then the sum of money K should be suitably discounted to reflect the time to expiry and the interest rate. However, S is not discounted as it represents the commodity itself, not a sum of money that can be invested.
The above equation can be modified to suit a time before expiry:
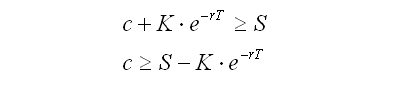
This is the lower bound of a call option’s price.
***
The lower bound for a put option can be derived in a similar fashion.
On the expiry date, someone who holds a put option and the commodity can choose to sell the commodity at the strike price (K) regardless of the market price (S) of the commodity.
Therefore, it follows that the put option plus the commodity is at least as valuable as the strike price (K).
On the expiry date, the value of a put option obeys the following correlation:
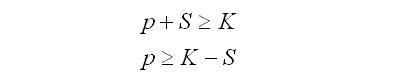
If it is not yet the expiry date, then the sum of money K should be suitable discounted by the time to expiry and the interest rate. However, S is not discounted as it represent the commodity itself, not a sum of money that can be invested.
The above equation can be modified to suit a time before expiry:

This is the lower bound of a put option’s price.
Price of a call option, c
Price of a put option, p
Strike price of option, K
Time to expiry, T
Current market price of underlying commodity, S
Risk-free continuously compounded interest rate, r
On the expiry date, someone who holds a call option and some cash equal to the strike price (K) can choose to buy the commodity at the fixed price K regardless of the market price (S) of the commodity. Obviously, if the market price turns out to be higher than the strike price, the buyer gets to buy at a lower price, which means the option is now worth a bundle of money. On the other hand, if the strike price is higher than market price, the holder will not exercise the option and the option is worth nothing.
Therefore, it follows that the call option plus K in cash is at least as valuable as the commodity’s market price (S). On the expiry date, the value of a call option obeys the following correlation:
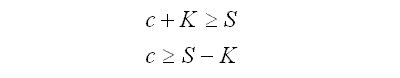
If it is not yet the expiry date, then the sum of money K should be suitably discounted to reflect the time to expiry and the interest rate. However, S is not discounted as it represents the commodity itself, not a sum of money that can be invested.
The above equation can be modified to suit a time before expiry:
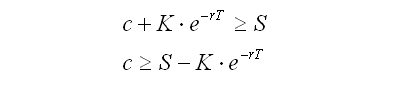
This is the lower bound of a call option’s price.
The lower bound for a put option can be derived in a similar fashion.
On the expiry date, someone who holds a put option and the commodity can choose to sell the commodity at the strike price (K) regardless of the market price (S) of the commodity.
Therefore, it follows that the put option plus the commodity is at least as valuable as the strike price (K).
On the expiry date, the value of a put option obeys the following correlation:
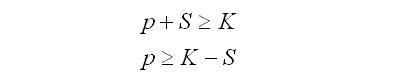
If it is not yet the expiry date, then the sum of money K should be suitable discounted by the time to expiry and the interest rate. However, S is not discounted as it represent the commodity itself, not a sum of money that can be invested.
The above equation can be modified to suit a time before expiry:

This is the lower bound of a put option’s price.
Labels: finance

<< Home