The engineer strikes back: a brief theoretical investigation in the design of vibrators (vaginal stimulation devices)
One of the housemates pointed me to this entry by Finicky Feline:
“She calls her thing brr brr brr!”
“Hmm, do those things pulsate?”
“Why are you asking me?”
While changing, I had a sudden flash of insight: the pulsations of a vibrator can be incorporated mechanically without the need for switching/oscillating electronics. I ran upstairs to explain to the housemate...
A commonly employed method to set up vibrations is to install a lop-sided piece of weight on a rotating shaft. For this application of pulsating vibrations, two eccentrically mounted (a fancy way of saying ‘unbalanced’) weights are required. The rotating weights are to be driven at similar but not identical speeds.
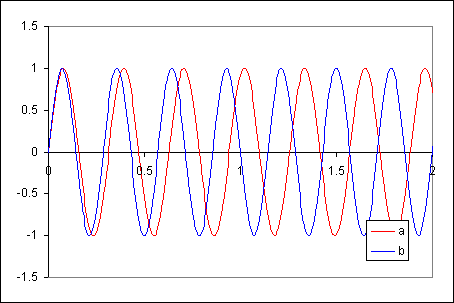
The force exerted (in the x-direction) by a rotating mass is sinusoidal. Because the two weights are rotated at slightly different speeds, the sinusoids have slightly different frequencies:
Side note:
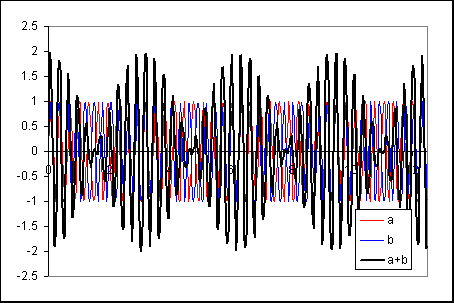
The combined effect of sinusoids of different frequencies (but identical amplitudes) exhibits a beating trend: the vibration frequency is the average of the two vibrations, while the beating frequency is the difference between the two vibrations.
Side note:
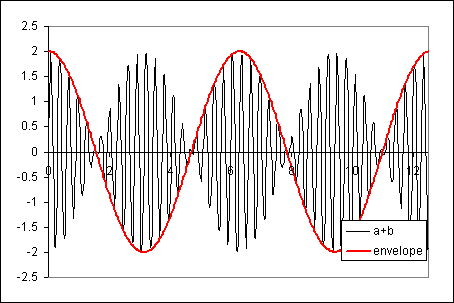
The following figure shows the combined vibration with an envelope equivalent to the frequency difference between the rotating masses:
Later, when I was washing dishes, the complication of the vibrator problem revealed itself. The vibration amplitude not only pulsates in the x direction, but also in the y direction. What’s more, the pulsations in the x-direction are out of phase with the pulsations in the y-direction.
Restricting the analysis to the x-direction gives a severely misleading picture of the vibration behavior of this hypothetical Brrbrrbrr. When observed in 2 dimensions, the behavior of the vibration is rather interesting.
The direction of vibration precesses (rotates slowly), the rate of precession being equal to the speed difference of the two rotating masses.
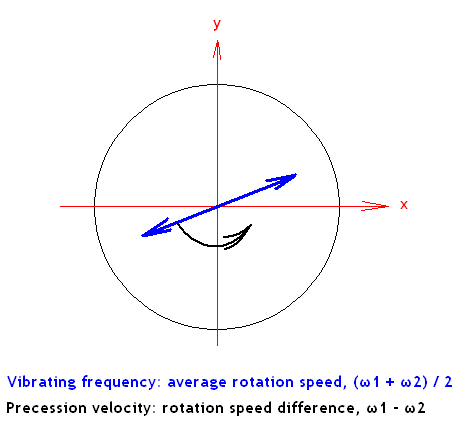
This is what gives the pulsations in the x and y directions. As the direction of vibration rotates to coincide with the x-direction, the amplitude of vibration is the greatest in the x-direction. When the direction of vibration is perpendicular to the x-direction, there is no amplitude in the x-direction. Hence, the x-vibration pulsates.
So it turns out that the pure pulsation I was searching for cannot be found in pairs of rotating masses. However, the pulsation can be restored by canceling vibrations in the y-direction, leaving only the x-direction to pulsate. This can be done by two pairs of rotating masses that rotate in opposite directions.

The arrangement shown above is designed so that the y-direction component of the centripetal forces are set up in opposing directions so that they contribute to a net of zero y-direction forces. But, the x-direction forces are arranged in the same direction, so that the x-direction vibration amplitude is doubled. And here, the analysis for uniaxial vibration (as presented above) can be applied, and pulsation is achieved.
Success!
With great sadness, I gave it one last kiss and threw it in the dustbin.
My brrbrrbrr, at 20 months of age, has died on me. Sputter sputter and then silence.
We had some ecstatic moments you and I.
But maybe it’s a blessing in disguise because I’ll finally need a man.
“She calls her thing brr brr brr!”
“Hmm, do those things pulsate?”
“Why are you asking me?”
While changing, I had a sudden flash of insight: the pulsations of a vibrator can be incorporated mechanically without the need for switching/oscillating electronics. I ran upstairs to explain to the housemate...
A commonly employed method to set up vibrations is to install a lop-sided piece of weight on a rotating shaft. For this application of pulsating vibrations, two eccentrically mounted (a fancy way of saying ‘unbalanced’) weights are required. The rotating weights are to be driven at similar but not identical speeds.
The force exerted (in the x-direction) by a rotating mass is sinusoidal. Because the two weights are rotated at slightly different speeds, the sinusoids have slightly different frequencies:

Side note:
The similar but non-identical speeds of these rotating weights can be easily designed by the use of gears. Shaft A (which holds mass a) can be connected to shaft B (which holds mass b) by a pair of gears. In the examples used here, the gear on shaft A has 22 teeth; the gear on shaft B has 20 teeth. A motor driving any of these shafts would drive both of them with the preset ratio of speeds.
The combined effect of sinusoids of different frequencies (but identical amplitudes) exhibits a beating trend: the vibration frequency is the average of the two vibrations, while the beating frequency is the difference between the two vibrations.

Side note:
The centripetal/centrifugal force (F) associated with an eccentric weight of mass M, eccentricity e (distance from shaft centerline to centre of mass) and rotation speed ω is of the following form:
F = M × ω / e
Given that the force amplitudes of both shafts are to be the same,
F1 = F2, and hence
M1 × ω1 / e1 = M2 × ω2 / e2
The following figure shows the combined vibration with an envelope equivalent to the frequency difference between the rotating masses:

Later, when I was washing dishes, the complication of the vibrator problem revealed itself. The vibration amplitude not only pulsates in the x direction, but also in the y direction. What’s more, the pulsations in the x-direction are out of phase with the pulsations in the y-direction.
Restricting the analysis to the x-direction gives a severely misleading picture of the vibration behavior of this hypothetical Brrbrrbrr. When observed in 2 dimensions, the behavior of the vibration is rather interesting.
The direction of vibration precesses (rotates slowly), the rate of precession being equal to the speed difference of the two rotating masses.

This is what gives the pulsations in the x and y directions. As the direction of vibration rotates to coincide with the x-direction, the amplitude of vibration is the greatest in the x-direction. When the direction of vibration is perpendicular to the x-direction, there is no amplitude in the x-direction. Hence, the x-vibration pulsates.
So it turns out that the pure pulsation I was searching for cannot be found in pairs of rotating masses. However, the pulsation can be restored by canceling vibrations in the y-direction, leaving only the x-direction to pulsate. This can be done by two pairs of rotating masses that rotate in opposite directions.

The arrangement shown above is designed so that the y-direction component of the centripetal forces are set up in opposing directions so that they contribute to a net of zero y-direction forces. But, the x-direction forces are arranged in the same direction, so that the x-direction vibration amplitude is doubled. And here, the analysis for uniaxial vibration (as presented above) can be applied, and pulsation is achieved.
Success!
Labels: applied mathematics, applied science, physics

<< Home