Avoiding bank charges and unfavourable buy/sell exchange rates for sending and receiving funds via telegraphic transfer (TT)

Note: This document was originally written to describe the procedures to the parties involved. However, seeing that this blog is suffering from an update-deficit, the posting of this document will serve to notify that the author is alive (and possibly well)


Currently, [name removed] (CYA) receives money from Malaysia, and Yee Wei (TYW) intends to send money to Malaysia. This document describes a way to reduce the transaction costs associated with the transfer of funds. Exchange rates based on Maybank’s exchange rates (24th August 2007) for TT. TT fees in Australia based on charges by the Commonwealth Bank. TT fees in Malaysia were obtained from my father.


When CYA’s parents send money, the bank in Malaysia charges a RM 27 fee for sending a TT. The exchange rate for converting RM to AU$ slightly high, meaning the bank takes a small proportion of the money as its profit for doing the currency exchange. The bank in Australia charges AU$15 for receiving a TT.

When TYW sends money to his parents, the bank in Australia charges a AU$22 fee for sending a TT. The exchange rate for converting AU$ to RM slightly lower, meaning the bank takes a small proportion of the money as its profit for doing the currency exchange. The bank in Malaysia charges RM5 for receiving a TT.

This pair of transactions can be represented as follows, using AU$3000 as the sum that is to be transferred:


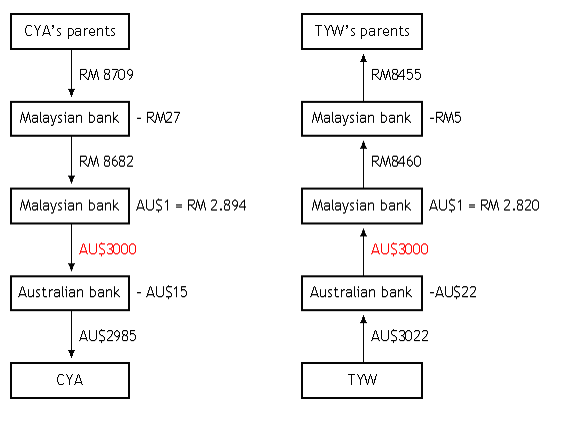
Note that the bank gives different exchange rates when changing the currency in different directions. Also observe that in both cases, AU$3000 was sent but in both cases, the sender sends more than AU$3000 and the recipient gets less than AU$3000.


An alternative way to transfer AU$3000 can be designed to eliminate all bank fees:
TYW pays CYA AU$3000
CYA’s parents pay TYW’s parents a sum in Ringgit that is equal to AU$3000

If the Ringgit equivalent of AU$3000 is based on the middle rate, then the exchange rate to be used is (2.820 + 2.894)/2 = 2.857, which is the average of the bank’s buy/sell rates.

Then,
TYW pays CYA AU$3000, and
CYA’s parents pay TYW’s RM 8571


The cash flow can be represented as:


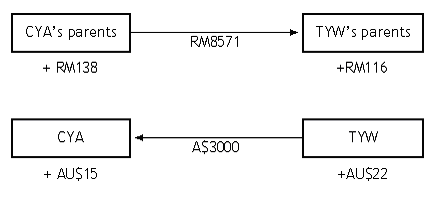
Note the savings/gains that each party gets as a result of not paying for the banks’ profits.

Compared to the cash flow which involved banks, every party gains a saving in the form of not paying bank fees and also not paying the buy/sell exchange rate difference.

The savings/gains are as follows:



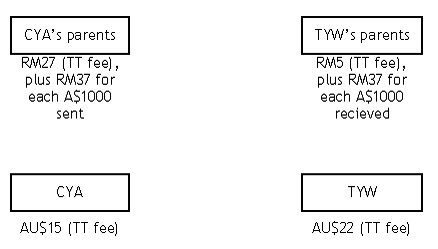
This scheme is not risk-free. There are risks of either of the payers (TYW or CYA’s parent) defaulting. The use of banks would virtually eliminate this risk at the cost of transaction fees.