A comparison between Newtonian and Relativistic models of simple oscillating systems
Special relativity will be discussed here, but it is best to learn special relativity from a proper text. While care has been taken to maintain accuracy, many of the important concepts in SR are not well represented here, especially the relativity part: relative to what?
A long time ago, I argued that rigid bodies do not exist. Here is a summary:
Rigid bodies are objects that have infinite stiffness. The question is, what sort of behaviour will be present when considering materials of large but finite stiffness?
In taking a small step to answering this question, I have constructed a simple model of 3 masses m1, m2 and m3; connected by two linear springs of stiffness ka and kb. In this mathematical model, the coordinates for the individual masses, x, y, and z have their origins at the respective masses’ equilibrium positions.
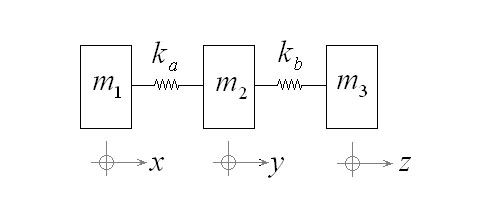
The differential equations of motion can be easily formulated using the simple F=ma relationship.
The differential equations for classical Newtonian mechanics are a set of 3 equations as such:
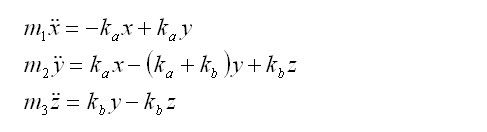
The system is then considered with Relativistic effects. The masses m1, m2 and m3 are called the rest mass, which is the mass measured when the system is stationary. As they move faster and faster approaching the speed of light, the measured mass becomes greater and greater, thus requiring more energy to accelerate. This is accounted for by a term γ that is multiplied with the rest mass.
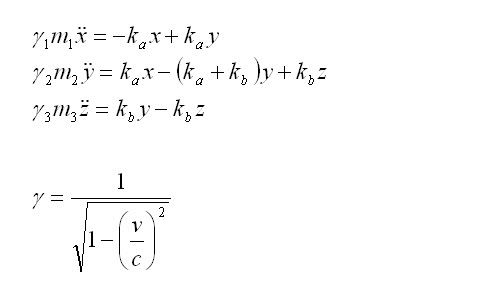
As one can observe from the above equation, when velocity v approaches the speed of light, γ approaches infinity. There is an infinitely high energy barrier that stands at the speed of light. Only massless particles, such as photons, may travel at light speed.
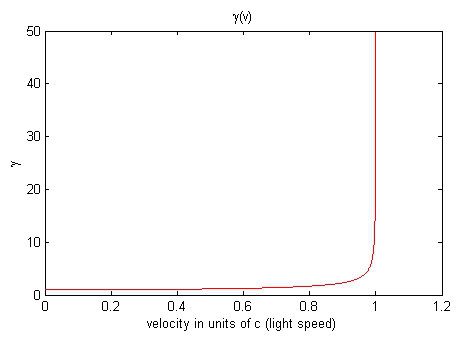
One important effect of γ on the equations of motion is that the mass becomes greater as speeds increase, such that the masses may never approach 300,000 km/s.
Having obtained the differential equations of motion, the motion is then simulated using the 4th order Rungge-Kutta algorithm with increment time intervals of 0.00001s.
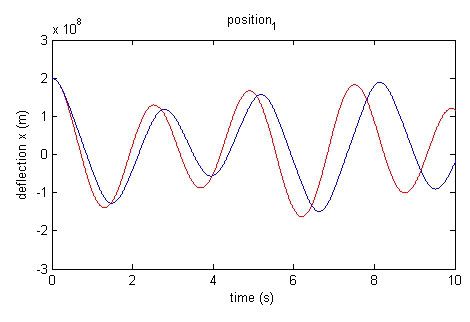
click here for a plot with a larger domain t=[0,20]
red: Newtonian
blue: Relativistic
The plots of the position of mass 1 using Newtonian and relativistic models are not significantly different to the naked eye.
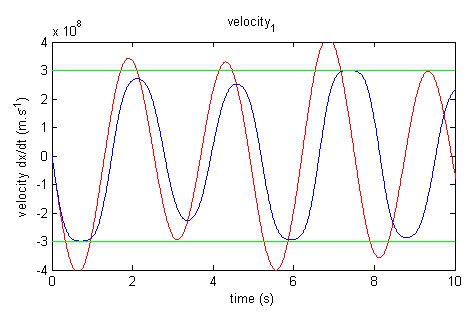
click here for a plot with a larger domain t=[0,20]
red: Newtonian
blue: Relativistic
green: light speed, c
However, the differences are clearly seen when the velocity plots are compared. The linear Newtonian model exhibits instances of violating the speed of light, while the relativistic one shows the energy barrier forbidding the speed to exceed 3x10^8 m/s.
Around the time of 1s, the Newtonian model shows speeds greater than c while the relativistic model remains bounded within c. Referring back to the position plot, this effect can be seen in the slope of the curves. The Newtonian model’s motion is faster, and the slope is thus steeper than the Relativistic model’s.
As a consequence, the frequency of oscillation in the relativistic model is lower than that present in the Newtonian model. Also, due to the nonlinear term γ, the Relativistic model does not exhibit sinusoidal motion.
Mathematics
A long time ago, I argued that rigid bodies do not exist. Here is a summary:
A rigid body’s length remains constant all the time. It cannot deform at all. Thus, when one pushes on one end of a rigid rod, the other end also moves at the same time. There is no delay between one end being pushed and the other end moving.
If we have a very long rod, and one end is pushed, at the same time, the other end will move. This process is instant.
However, a beam of light shined from the other end requires finite time to traverse the length of the rod. That being the case, it would seem that by pushing on long rods, information can be sent faster than the speed of light.
Of course, that is impossible. Thus, rigid bodies do not exist. Everything in this universe, from neutron stars to diamond gemstones, are not rigid; they are elastic. All of them.
Related links:
Rigid bodies violate special relativity
Real materials as opposed to rigid bodies
Rigid bodies are objects that have infinite stiffness. The question is, what sort of behaviour will be present when considering materials of large but finite stiffness?
In taking a small step to answering this question, I have constructed a simple model of 3 masses m1, m2 and m3; connected by two linear springs of stiffness ka and kb. In this mathematical model, the coordinates for the individual masses, x, y, and z have their origins at the respective masses’ equilibrium positions.
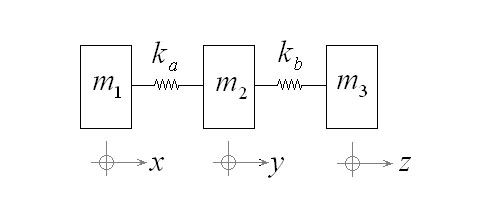
The differential equations of motion can be easily formulated using the simple F=ma relationship.
The differential equations for classical Newtonian mechanics are a set of 3 equations as such:
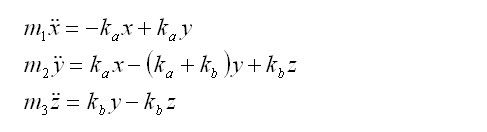
The system is then considered with Relativistic effects. The masses m1, m2 and m3 are called the rest mass, which is the mass measured when the system is stationary. As they move faster and faster approaching the speed of light, the measured mass becomes greater and greater, thus requiring more energy to accelerate. This is accounted for by a term γ that is multiplied with the rest mass.
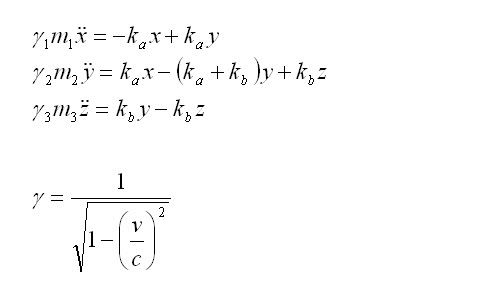
As one can observe from the above equation, when velocity v approaches the speed of light, γ approaches infinity. There is an infinitely high energy barrier that stands at the speed of light. Only massless particles, such as photons, may travel at light speed.
One important effect of γ on the equations of motion is that the mass becomes greater as speeds increase, such that the masses may never approach 300,000 km/s.

Having obtained the differential equations of motion, the motion is then simulated using the 4th order Rungge-Kutta algorithm with increment time intervals of 0.00001s.

click here for a plot with a larger domain t=[0,20]
red: Newtonian
blue: Relativistic
The plots of the position of mass 1 using Newtonian and relativistic models are not significantly different to the naked eye.

click here for a plot with a larger domain t=[0,20]
red: Newtonian
blue: Relativistic
green: light speed, c
However, the differences are clearly seen when the velocity plots are compared. The linear Newtonian model exhibits instances of violating the speed of light, while the relativistic one shows the energy barrier forbidding the speed to exceed 3x10^8 m/s.
Around the time of 1s, the Newtonian model shows speeds greater than c while the relativistic model remains bounded within c. Referring back to the position plot, this effect can be seen in the slope of the curves. The Newtonian model’s motion is faster, and the slope is thus steeper than the Relativistic model’s.
As a consequence, the frequency of oscillation in the relativistic model is lower than that present in the Newtonian model. Also, due to the nonlinear term γ, the Relativistic model does not exhibit sinusoidal motion.
Mathematics
Labels: applied mathematics, natural science, physics

<< Home