The elegance of mathematics
I’ve been trying to count the number of elementary operations f(k) needed to compute the determinant of a k x k matrix of real elements.
This is the general form for the number of elementary operations:
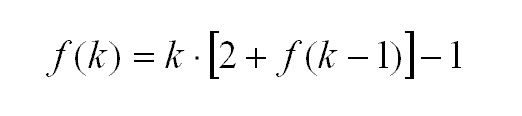
Since this is a recursive function, we need to define the first case, which is the trivial case of a one-element matrix: f(1) = 0. The determinant is simply the value of the element, and no operations are necessary to arrive at this conclusion.
Now for the bragging bit. I managed to reduce the recursive function into a more manageable function that can be computed without knowledge of f(k-1).
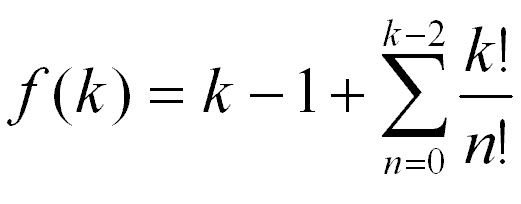
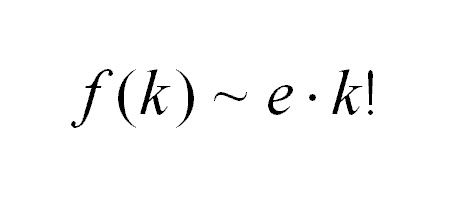
Appendix
Re-expressing the function by removing k! from the summation:
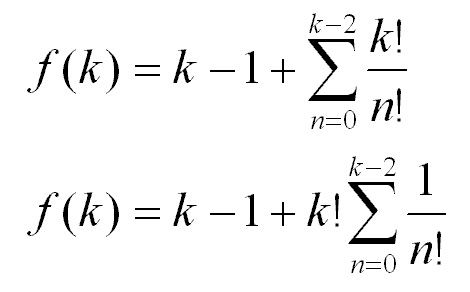
Interestingly, the constant e can also be defined as such:
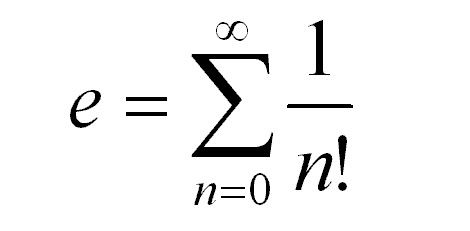
But the series is a sum of infinitely many terms, as compared to f(k) which has only k terms. Thus a finite series such as that found in f(k) does not actually equal e, but converges towards e.
Comparing the definition of e with f(k):
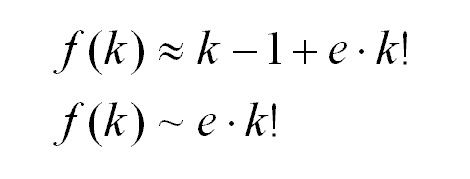
The growth rate of the factorial term is so fast that it very rapidly overwhelms the (k-1) term, and thus (k-1) can be dropped from the approximation. To illustrate the difference in scale using k=15:
k-1 = 15-1 = 14
k! = 15 x 14 x 13 x … x 2 x 1 = 1.3 x 10^12 (there are 13 digits in this number)
Mathematics
This is the general form for the number of elementary operations:
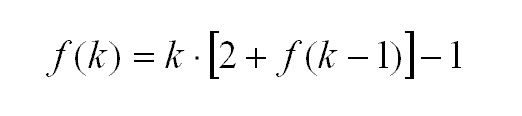
Since this is a recursive function, we need to define the first case, which is the trivial case of a one-element matrix: f(1) = 0. The determinant is simply the value of the element, and no operations are necessary to arrive at this conclusion.
Now for the bragging bit. I managed to reduce the recursive function into a more manageable function that can be computed without knowledge of f(k-1).
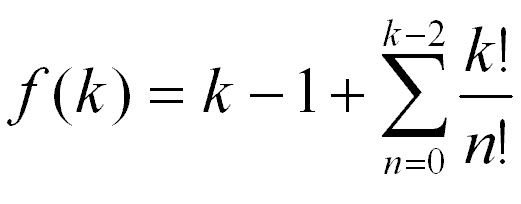
Further investigation and lucky breaks has revealed that f(k) converges to e*k! (e = 2.172818…) very rapidly. At k=18, it is accurate to within 15 significant figures. At k=19, the accuracy is at least 30 significant figures.
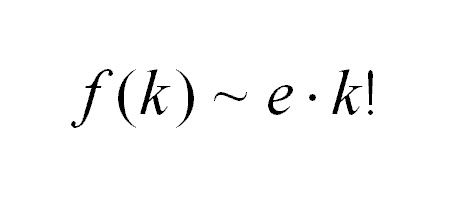
Appendix
Re-expressing the function by removing k! from the summation:
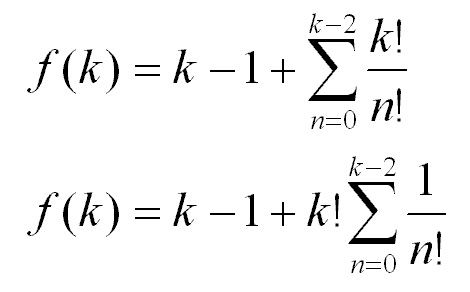
Interestingly, the constant e can also be defined as such:
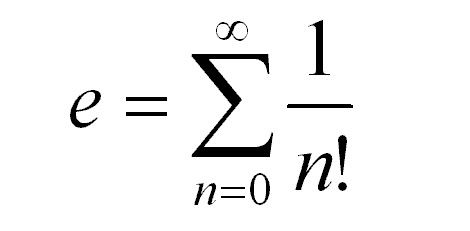
But the series is a sum of infinitely many terms, as compared to f(k) which has only k terms. Thus a finite series such as that found in f(k) does not actually equal e, but converges towards e.
Comparing the definition of e with f(k):
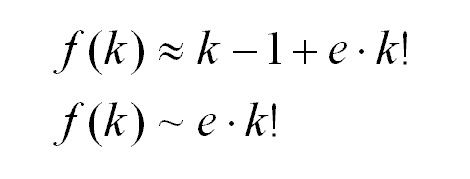
The growth rate of the factorial term is so fast that it very rapidly overwhelms the (k-1) term, and thus (k-1) can be dropped from the approximation. To illustrate the difference in scale using k=15:
k-1 = 15-1 = 14
k! = 15 x 14 x 13 x … x 2 x 1 = 1.3 x 10^12 (there are 13 digits in this number)
Mathematics
Labels: mathematics

<< Home