Physics very hard meh?

In the course of one’s education, it is perhaps inevitable that one would come upon remarks of this nature: “Mathematics/physics/chemistry is such a difficult subject! There is only one correct answer. If I mess up somewhere along the way then I’ll definitely get it wrong. No middle route between correct and wrong. That’s why I prefer economics/sejarah/marketing.”

Of course, most of these remarks are not as elegantly phrased as my example; they usually come in the form of semi-coherent moans and complaints.

If anyone had thought they could scrape through physics by plainly memorising equations, they would have either been wrong or possessed a very good memory.

While there is only one answer to a properly phrased problem, this solution can be approached from more than one way. Let’s illustrate this by considering a very common problem found in SPM-level physics.

A ball is rolled over a horizontal, rough surface with an initial velocity of 5 m/s. Friction will cause the ball to decelerate at a constant rate of 0.5 m/s2. Calculate the distance travelled by the ball in the first 7 seconds.

The first equation that comes to mind would be s = 0.5at^2 + ut. Where in our case a= -0.5, t= 7, u= 5. What if the nervous problem solver cannot remember the equation in full? Is she fucked?

Hell no! At least, not if she has some creativity.

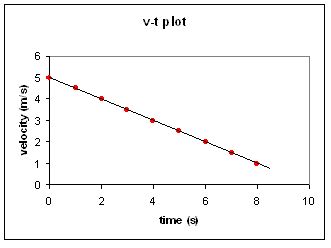
From an extensive knowledge of SPM-level calculus, she knows that displacement is the area under the curve of a velocity-time graph. And so she plots the graph. At t=0, v=5; at t=1, v=4.5; at t=2, v=4…and so on till t=7, v=1.5. It turns out to be a straight line with a slope of -0.5 and intersecting the v-axis at 5.




And thus, using some fundamental geometry, she calculates the area below the v-t plot from t=0 to t=7. Splitting the area into a rectangle and triangle, their respective areas are 7 x 1.5 and 0.5*3.5*7. Thus the total distance travelled is 22.75

This method being too absurdly simple, she tries to find the area properly by means of integration. Having already seen the velocity-time plot, she can express it as an equation v= -0.5t + 5. The area under v between the bounds of t=0 and t=7 can be found by integrating v with respect to t with the limits t=0 and t=7.

After integrating and before substitution of the limits, she notices something that will change her life forever:



That’s the equation! s = 0.5at^2 + ut. That equation is derived from this integral, and fitted for a lower limit of t=0. I’ve got it! Woot!

When I saw the similarities back in 2000, I was rather excited as well. My fellow students thought it was too much trouble. Probably because they already had the equation memorised to perfection.



Endgame:
Now that you've seen the equations, here is an extension of the problem given above. See if you can get it right.

Calculate the distance travelled by the ball in the first 12 seconds.

Sounds easy? Have a go.
Hint: substituting t=12 into s = 0.5at^2 + ut does not work. v(t) is a piecewise continuous function.