Karatsuba Multiplication
In February, one of my father’s friends who in the automotive industry offered him an Audi A4 over several days for a test drive. After some nagging on my part, Dad accepted the offer and the car was delivered to our house. That’s the benefit of having someone high up in the ladder- they can arrange for test cars to be sent to your house, and for several days too.
The A4was is a brilliant car.
[Truncated- endless technically oriented drone regarding powerful 1.8 turbocharged engine, remarkable built quality, luxury, attention to detail…]
For those few days, we had 3 cars in the house. Dad used his usual Mercedes E280 to work (he wasn’t really into this A4 thing anyway; it was me who egged him into submission), Mom continued using the Toyota Prado (she wasn’t a big fan of this test drive thing too). Guess who had exclusive use of the A4?
[Truncated- endless gush about the excellent cabin built quality, soft-touch plastics, excellently damped control knobs, remarkable attention to detail, cup-holder…]
[Omitted- my peers’ (brothers, cousins, friends) reaction to the A4]
One fine day when I was visiting some lecturers in Taylor’s College, I parked the car in an inappropriate location. When I got back I noticed that I had been fined. Subang Jaya being the arsehole of a municipality it was, charged a hefty RM 80.00. I had to pay this fine- it was not my car, and if any action was taken, it would make me, my father & my father’s friend look like a bunch of kiamsiap idiots.
And thus I went to pay that stupid fine. I have only myself to blame.
It was crowded, and I had to wait. Having neglected to bring some reading material, I resorted to mental exercises to keep myself occupied. Taking two random, 2 digit numbers, I would multiply them mentally, and check the answer using my phone’s calculator. I was having such fun that the wait did not seem too long.
Karatsuba multiplication
[The following is a mathematics intensive discourse. Knowledge of lower secondary mathematics assumed]
The Karatsuba and Ofman algorithm to 2 digit multiplication is particularly suited to mental calculations compared to mentally doing it the long way using the plain, pencil & paper method we were taught in primary school.
Suppose we have 2 two-digit numbers we want to multiply (each digit represented by an alphabet):
ab x cd
We can rewrite the multiplication by separating the digits:
(10a + b) x (10c + d)
Putting these 2 numbers aside, we now go on to consider two similar systems:
(aZ + b) x (cZ + d)= ac*Z^2 + (ad + bc)Z + bd
Expanding the expression, we see that the middle term (ad + bc) might pose some problems
(a + b)(c + d) = ac + (ad + bc) + ac
(ad + bc) = (a + b)(c + d) - ac - bd
Expanding the expression and re-expressing the equation, we have a potential solution to the (ad + bc) problem in the previous equation above.
Comparing the two-digit multiplication with the generic quadratic equation by letting Z = 10:
(10a + b)(10c + d) = 100ac + 10(ad + bc) + bd
Recall that the problematic middle term (ad + bc) term can be expressed as (a+b)(c+d) – ac – bd.
Thus, the foundations to Karatsuba multiplication have been laid. The following example should illustrate some of the conveniences of the Karatsuba algorithm.
Lets multiply 97 by 56.
Add the digits in the first and second numbers, and multiply them:
(9+7) x (5+6) = 16 x 11 = 176
Multiply the first digits of each number:
9 x 5 = 45
Multiply the second digit of each number:
7 x 6 = 42
Deduct the product of first digits and the product of second digits from the product of the sum of digits:
176 – 45 – 42 = 89. That’s the middle term.
Thus 97 x 56 = 100 * (the product of first digits) + 10 * (the middle term) + (the product of last digits)
To mentally add them, just offset each number by one digit and sum them:
Have fun!
[This algorithm will be of no use to practitioners of abacus-based mental arithmetic who can perform many two-digit multiplications in a few seconds.]
Comparison between Karatsuba multiplication and long multiplication
Using the example above, 97 x 56, long division will have us perform the following operations:
97 x 6 = (6 x 7) + 10(6 x 9) = 42 + 540 = 582
97 x 5 = (5 x 7) + 10(5 x 9) = 35 + 450 = 485
97 x 56 = 582 + 4850 = 5432
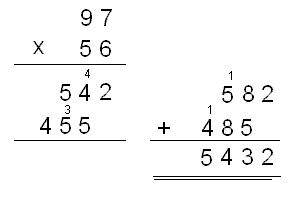
The problem associated with long multiplication is the need to remember long and numbers while calculating other long numbers. Addition of these numbers usually involve carrying remainders over, adding to our troubles. In my experience, it’s the process of storing and recalling these numbers that usually makes mental long multiplication a tediously slow process.
Using Karatsuba on the same numbers, the operations are required:
Important numbers have been marked using capital letters.
9 + 7 = 16
5 + 6 = 11
16 x 11 = 176 (A)
9 x 5 = 45 (B)
7 x 6 = 42 (C)
176 – 42 – 45 = 89 (D)
97 x 56 = 4500 + 890 + 42 = 5432
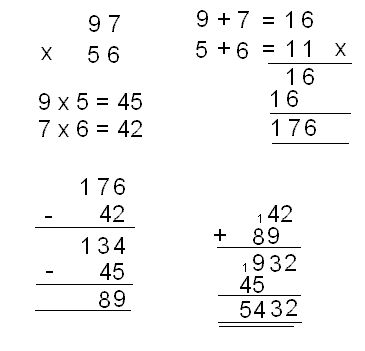
In this example, the numbers are reasonably large, and the sums of digits are in two digits (16 & 11). However, we are always summing 2 numbers less than 9, thus if they turn out to be 2 digits, the first one will always be 1. This summation of digits should be a trivial task.
Multiplying the digits should not be too difficult: we are already equipped with look-up tables to multiply any natural numbers from [0,0] to [12,12]. And as stated above, the first digit of a two-digit sum will always be 1. Remember this product of sum of digits (call it number A)
Multiplying the first digits and last digits is a trivial task and should take no time at all. These will be called numbers B and C.
Subtract B and C from A. This will probably be the most intense operation. However, it can be drastically simplified by doing the subtraction in 2 steps. For examples, 176 – 42 = 176 – 40 – 2 = 134, or 85 – 47 = 85 – 50 + 3 = 38. This will reduce the complexity of calculations to semi-trivial problems that already have look-up tables stored in memory, thus eliminating the need to remember carried numbers and whatever. Call the subtracted number A – B – C = D. The number A is no longer needed, and can be deleted.
Add 100B + 10D + C. Add 10D + C first by mentally offsetting the digits, then add 100B to by offsetting the digits of B by 2 steps. If by now you have forgotten the numbers B and C, it is no problem because they can be obtained trivially by looking at the digits of the original number to be multiplied.
Karatsuba is hideously complicated to describe in words, but when you manipulate the numbers in your mind, things fall into place with surprising ease. Note that all operations involve small numbers with very little of the nasty carrying business.
With a pencil and paper, long multiplication is generally faster because the business of reading and writing avoids the need for slow remember and recall processes.
This is where the abacus will trounce long and Karatsuba multiplication- the read/write operations are sometimes skipped altogether and the processes are just added. For example, adding 1 and 2 does not require the user to read the existing 1, add 2 to it, and write 3. The user simply dumps 2 more into the existing pile, and 3 is the automatic result. At any rate, the read/write speeds are phenomenally fast anyway.
Application of Karatsuba multiplication in simplifying huge multiplications
Say we need to multiply 2 sixteen-digit numbers. Long multiplication will require that we multiply all digits in the first number with all digits in the second number and sum them accordingly. It should be clear now that we will need to perform 16 x 16 = 256 one-digit multiplications.
If we express the 16 digit number abcdefghijklmnop as abcdefgh*100000000 + iklmnopq and repeat for the other 16-digit number, the Karatsuba algotith can be applied. Now, there will be 3 multplications of eight-digit numbers, and thus require only 3 x 8 x 8 = 195 one-digit multiplications. Or, to take it another step further, each eight-digit multiplication can be broken into a set of 3 four-digit multiplications., reducing the number of one-digit multiplications to a mere 3 x 3 x 4 x 4 = 144. However, there is the cost of the additional subtraction and addition steps, and care should be taken to avoid overdoing the recursive Karatsuba.
This lesson in number theory brought to you by Yee Wei.
ps. what a bloody long post! MS Word estimates it to be 1500 words.
Congratulations if you have reached the end. Just for fun, please drop me a note in the comments section to tell me that you've reached The End.
The A4
[Truncated- endless technically oriented drone regarding powerful 1.8 turbocharged engine, remarkable built quality, luxury, attention to detail…]
For those few days, we had 3 cars in the house. Dad used his usual Mercedes E280 to work (he wasn’t really into this A4 thing anyway; it was me who egged him into submission), Mom continued using the Toyota Prado (she wasn’t a big fan of this test drive thing too). Guess who had exclusive use of the A4?
[Truncated- endless gush about the excellent cabin built quality, soft-touch plastics, excellently damped control knobs, remarkable attention to detail, cup-holder…]
[Omitted- my peers’ (brothers, cousins, friends) reaction to the A4]
One fine day when I was visiting some lecturers in Taylor’s College, I parked the car in an inappropriate location. When I got back I noticed that I had been fined. Subang Jaya being the arsehole of a municipality it was, charged a hefty RM 80.00. I had to pay this fine- it was not my car, and if any action was taken, it would make me, my father & my father’s friend look like a bunch of kiamsiap idiots.
And thus I went to pay that stupid fine. I have only myself to blame.
It was crowded, and I had to wait. Having neglected to bring some reading material, I resorted to mental exercises to keep myself occupied. Taking two random, 2 digit numbers, I would multiply them mentally, and check the answer using my phone’s calculator. I was having such fun that the wait did not seem too long.
Karatsuba multiplication
[The following is a mathematics intensive discourse. Knowledge of lower secondary mathematics assumed]
The Karatsuba and Ofman algorithm to 2 digit multiplication is particularly suited to mental calculations compared to mentally doing it the long way using the plain, pencil & paper method we were taught in primary school.
Suppose we have 2 two-digit numbers we want to multiply (each digit represented by an alphabet):
ab x cd
We can rewrite the multiplication by separating the digits:
(10a + b) x (10c + d)
Putting these 2 numbers aside, we now go on to consider two similar systems:
(aZ + b) x (cZ + d)= ac*Z^2 + (ad + bc)Z + bd
Expanding the expression, we see that the middle term (ad + bc) might pose some problems
(a + b)(c + d) = ac + (ad + bc) + ac
(ad + bc) = (a + b)(c + d) - ac - bd
Expanding the expression and re-expressing the equation, we have a potential solution to the (ad + bc) problem in the previous equation above.
Comparing the two-digit multiplication with the generic quadratic equation by letting Z = 10:
(10a + b)(10c + d) = 100ac + 10(ad + bc) + bd
Recall that the problematic middle term (ad + bc) term can be expressed as (a+b)(c+d) – ac – bd.
Thus, the foundations to Karatsuba multiplication have been laid. The following example should illustrate some of the conveniences of the Karatsuba algorithm.
Lets multiply 97 by 56.
Add the digits in the first and second numbers, and multiply them:
(9+7) x (5+6) = 16 x 11 = 176
Multiply the first digits of each number:
9 x 5 = 45
Multiply the second digit of each number:
7 x 6 = 42
Deduct the product of first digits and the product of second digits from the product of the sum of digits:
176 – 45 – 42 = 89. That’s the middle term.
Thus 97 x 56 = 100 * (the product of first digits) + 10 * (the middle term) + (the product of last digits)
To mentally add them, just offset each number by one digit and sum them:
4500
890
+ 42
5432
890
+ 42
5432
Have fun!
[This algorithm will be of no use to practitioners of abacus-based mental arithmetic who can perform many two-digit multiplications in a few seconds.]
Comparison between Karatsuba multiplication and long multiplication
Using the example above, 97 x 56, long division will have us perform the following operations:
97 x 6 = (6 x 7) + 10(6 x 9) = 42 + 540 = 582
97 x 5 = (5 x 7) + 10(5 x 9) = 35 + 450 = 485
97 x 56 = 582 + 4850 = 5432
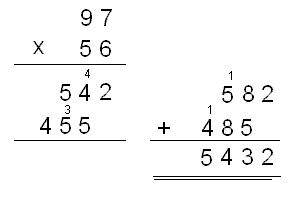
The problem associated with long multiplication is the need to remember long and numbers while calculating other long numbers. Addition of these numbers usually involve carrying remainders over, adding to our troubles. In my experience, it’s the process of storing and recalling these numbers that usually makes mental long multiplication a tediously slow process.
Using Karatsuba on the same numbers, the operations are required:
Important numbers have been marked using capital letters.
9 + 7 = 16
5 + 6 = 11
16 x 11 = 176 (A)
9 x 5 = 45 (B)
7 x 6 = 42 (C)
176 – 42 – 45 = 89 (D)
97 x 56 = 4500 + 890 + 42 = 5432
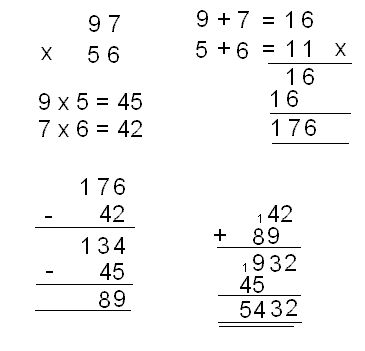
In this example, the numbers are reasonably large, and the sums of digits are in two digits (16 & 11). However, we are always summing 2 numbers less than 9, thus if they turn out to be 2 digits, the first one will always be 1. This summation of digits should be a trivial task.
Multiplying the digits should not be too difficult: we are already equipped with look-up tables to multiply any natural numbers from [0,0] to [12,12]. And as stated above, the first digit of a two-digit sum will always be 1. Remember this product of sum of digits (call it number A)
Multiplying the first digits and last digits is a trivial task and should take no time at all. These will be called numbers B and C.
Subtract B and C from A. This will probably be the most intense operation. However, it can be drastically simplified by doing the subtraction in 2 steps. For examples, 176 – 42 = 176 – 40 – 2 = 134, or 85 – 47 = 85 – 50 + 3 = 38. This will reduce the complexity of calculations to semi-trivial problems that already have look-up tables stored in memory, thus eliminating the need to remember carried numbers and whatever. Call the subtracted number A – B – C = D. The number A is no longer needed, and can be deleted.
Add 100B + 10D + C. Add 10D + C first by mentally offsetting the digits, then add 100B to by offsetting the digits of B by 2 steps. If by now you have forgotten the numbers B and C, it is no problem because they can be obtained trivially by looking at the digits of the original number to be multiplied.
Karatsuba is hideously complicated to describe in words, but when you manipulate the numbers in your mind, things fall into place with surprising ease. Note that all operations involve small numbers with very little of the nasty carrying business.
With a pencil and paper, long multiplication is generally faster because the business of reading and writing avoids the need for slow remember and recall processes.
This is where the abacus will trounce long and Karatsuba multiplication- the read/write operations are sometimes skipped altogether and the processes are just added. For example, adding 1 and 2 does not require the user to read the existing 1, add 2 to it, and write 3. The user simply dumps 2 more into the existing pile, and 3 is the automatic result. At any rate, the read/write speeds are phenomenally fast anyway.
Application of Karatsuba multiplication in simplifying huge multiplications
Say we need to multiply 2 sixteen-digit numbers. Long multiplication will require that we multiply all digits in the first number with all digits in the second number and sum them accordingly. It should be clear now that we will need to perform 16 x 16 = 256 one-digit multiplications.
If we express the 16 digit number abcdefghijklmnop as abcdefgh*100000000 + iklmnopq and repeat for the other 16-digit number, the Karatsuba algotith can be applied. Now, there will be 3 multplications of eight-digit numbers, and thus require only 3 x 8 x 8 = 195 one-digit multiplications. Or, to take it another step further, each eight-digit multiplication can be broken into a set of 3 four-digit multiplications., reducing the number of one-digit multiplications to a mere 3 x 3 x 4 x 4 = 144. However, there is the cost of the additional subtraction and addition steps, and care should be taken to avoid overdoing the recursive Karatsuba.
This lesson in number theory brought to you by Yee Wei.
ps. what a bloody long post! MS Word estimates it to be 1500 words.
Congratulations if you have reached the end. Just for fun, please drop me a note in the comments section to tell me that you've reached The End.

<< Home