An introduction to income tax for the mathematically-inclined (calculus is required)
In almost all countries, the payable income tax depends on the individual’s taxable income earned in the financial year.
Generally, the tax rates are quoted as marginal rates for different income brackets. The Hong Kong marginal tax rates for different income levels is shown below:
In this analysis of income tax, the concept of marginal tax is of great importance. At a marginal tax rate of 5%, each additional dollar earned will result in an additional 5 cents of tax.
We will now use the following notation: x is the income earned, and T is the total tax payable, and r is the marginal tax rate.
From the preceding statement, it is shown that the additional tax payable, ΔT, is a multiple of the tax rate, r, and the additional income, Δx:

As the above manipulation shows, the marginal tax rate is the rate of change of total payable tax with respect to income.
As the example of Hong Kong’s marginal rates, income is taxed at different rates. The first few thousand will generally be taxed at a very low marginal rate, and the subsequent thousands taxed at a higher marginal rates. To find the total tax payable (as any income earner would like to know), one procedure is to use the Riemann integral:

Essentially, what this shows is that each dollar earned will be taxed at the marginal tax rate that applies for that dollar. The total tax payable is the sum of all products of individual dollars and respective marginal tax rates.
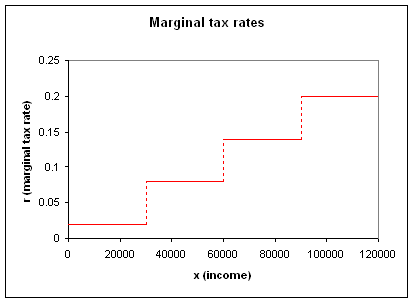
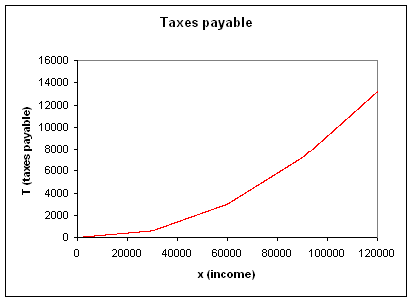
A comparison between the above charts will verify that T(x) is the definite integral of r(x) with limits 0 and x. The slope of T(x) changes when r(x) changes, which is not surprising given that a greater marginal rate implies a faster increase in the total taxes.
As the marginal tax rate is always non-negative (many countries have a zero-tax bracket for the first thousands earned), the total tax payable increases monotonically with income. That is to say, and increase in income will NEVER cause a decrease in payable tax.
Because the tax payable is an integral of a continuously defined function, the tax payable is a continuous function. While the rate of increase of the payable tax might change due to a change in the marginal tax rate, the tax payable will never take a discontinuous jump. Thus in systems using the marginal tax rate system, there is no dramatic taxation advantage in earning a few dollars more/less to try to squeeze into a different tax bracket.
End note
In the system of taxes, money is can only exist in discrete quantities. Certain taxation systems will require income to be rounded to the closest dollar, others will accept the income quoted in dollars and cents. Regardless, there exists a smallest unit in which money can be counted, be it dollar or cent.
Thus, the use of discrete calculus would be proper instead of real (continuous) calculus as done above.
The differential equation r(x) = dT/dx will no longer apply, and the following will take its place:

where Δx is the discrete currency unit.
Generally, the tax rates are quoted as marginal rates for different income brackets. The Hong Kong marginal tax rates for different income levels is shown below:
The first $30,000 will be taxed at 2%
The 30,001st to 60,000th dollar will be taxed at 8%
The 60,001st to 90,000th dollar will be taxed at 14%
Subsequent income above $90,000 will be taxed at 20%
In this analysis of income tax, the concept of marginal tax is of great importance. At a marginal tax rate of 5%, each additional dollar earned will result in an additional 5 cents of tax.
We will now use the following notation: x is the income earned, and T is the total tax payable, and r is the marginal tax rate.
From the preceding statement, it is shown that the additional tax payable, ΔT, is a multiple of the tax rate, r, and the additional income, Δx:

As the above manipulation shows, the marginal tax rate is the rate of change of total payable tax with respect to income.
As the example of Hong Kong’s marginal rates, income is taxed at different rates. The first few thousand will generally be taxed at a very low marginal rate, and the subsequent thousands taxed at a higher marginal rates. To find the total tax payable (as any income earner would like to know), one procedure is to use the Riemann integral:

Essentially, what this shows is that each dollar earned will be taxed at the marginal tax rate that applies for that dollar. The total tax payable is the sum of all products of individual dollars and respective marginal tax rates.


A comparison between the above charts will verify that T(x) is the definite integral of r(x) with limits 0 and x. The slope of T(x) changes when r(x) changes, which is not surprising given that a greater marginal rate implies a faster increase in the total taxes.
As the marginal tax rate is always non-negative (many countries have a zero-tax bracket for the first thousands earned), the total tax payable increases monotonically with income. That is to say, and increase in income will NEVER cause a decrease in payable tax.
Because the tax payable is an integral of a continuously defined function, the tax payable is a continuous function. While the rate of increase of the payable tax might change due to a change in the marginal tax rate, the tax payable will never take a discontinuous jump. Thus in systems using the marginal tax rate system, there is no dramatic taxation advantage in earning a few dollars more/less to try to squeeze into a different tax bracket.
End note
In the system of taxes, money is can only exist in discrete quantities. Certain taxation systems will require income to be rounded to the closest dollar, others will accept the income quoted in dollars and cents. Regardless, there exists a smallest unit in which money can be counted, be it dollar or cent.
Thus, the use of discrete calculus would be proper instead of real (continuous) calculus as done above.
The differential equation r(x) = dT/dx will no longer apply, and the following will take its place:

where Δx is the discrete currency unit.
Labels: applied mathematics, finance

<< Home