10's complement- an algorithm to fast subtraction
Sometime is my life, I read about a numerical method for use in subtraction. It’s called the 10’s complement, and the mechanism allows the addition algorithm to perform subtraction, with a little modification.
A brief comparison of addition and subtraction algorithms will be compared:
For addition, the procedure is simple. Add the right most digits, and carry excess 10s over to the next digit and continue the addition process digit-by-digit till completion.
For subtraction, the procedure is not a simple right-to-left operation. The borrowing of deficient 10s is performed before the subtraction of the digits, and if there is a series of zeros in the number, the borrowing will have to continue left until a non-zero digit is reached, and all these zeros will have to be changed to nines. Subtraction operations require read and write operations that move in a zigzag fashion.
The 10’s complement addresses this annoying issue of zigzagging areas of attention by introducing a simple subtraction step before performing an addition step.
Illustrating with the following example:
5006002 – 209137
Doing it using the long subtraction way (the normal way):
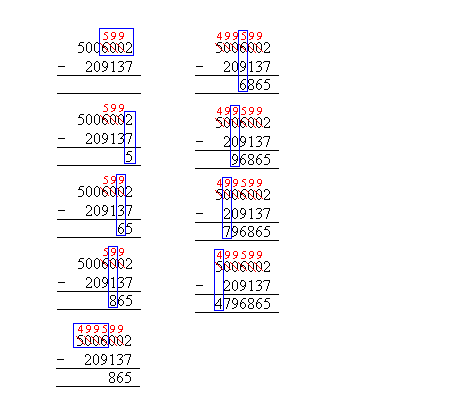
Subtraction of the right-most digits require a borrowed 10 from the digits on the left, thus changing 3 digits on the left. The subtraction process then returns to the first digit and the progressing on to the next.
Of course, the borrowing of 3 digits is consists of 3 distinct steps. If the next number is not capable of providing a 10, in the case of a zero, then the subsequent number will have to be considered until the first non-zero is reached.
The fourth digits also require a borrowed 10, and another 3 digits on the left have to be modified before returning to the actual subtraction.
As one can see, the areas of consideration while going through the subtraction process moves in a saw tooth fashion with intermittent hops left and right.
The 10s complement takes advantage of the fact that 209137 (the subtrahend- the number that is to be removed from 5006002, the minuend) is 999999 – 790862.
209137 = 999999 – 790862
209137 = 999999 – 790862 + 1 – 1
209137 = 1000000 – 790862 – 1
With this in mind, the subtraction can be rewritten as follows:
5006002 – 209137 = 5006002 – (1000000 – 790862 – 1)
5006002 – 209137 = 5006002 + 790862 + 1 – 1000000
The actual calculation procedure is shown below. Doubtless, there are more steps compared to long subtraction, but the business of borrowing is completely eliminated.
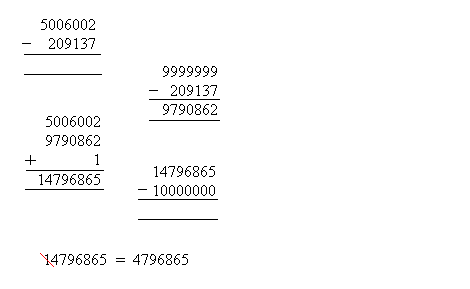
First, the complement of the subtrahend is taken. Sufficiently many digits of 9s must be used as to match the longest string present in the calculation. This is to ensure that the end result can be obtained simply by truncating the most significant digit from the answer.
The minuend is then added to one and the complement of the subtrahend.
Finally, a power of 10 is removed from the sum. If the number of 9’s used in the complementing process is a good choice, this final subtraction is a mere removal of the leading 1, as is the case here.
The explanation and derivation is unwieldy, but when performed with a sheet of paper and a pencil, the 10s complement method is an extremely easy method to reliably calculate subtractions of large numbers.
When working with binary numbers, the complement method is even more effective. This can be justified by the fact that the 2’s complement of binary numbers is trivial to perform.
This is because the complement is done by taking the difference of each digit with the largest number available in the base system, in the case of binary, one.
Due to the fact that 1 – 0 = 1 and 1 – 1 =0, taking the complement of each digit is exactly the same as flipping 1’s to 0’s and vice versa.
Working with binary numbers, here is another example:
110110 – 101
111111 – 000101 = 111010 (bit flipping of the subtrahend, 101)
110110 + 111010 + 1 = 1110001
1110001 – 1000000 = 110001
Therefore, 110110 – 101 = 110001
Mathematics
A brief comparison of addition and subtraction algorithms will be compared:
For addition, the procedure is simple. Add the right most digits, and carry excess 10s over to the next digit and continue the addition process digit-by-digit till completion.
For subtraction, the procedure is not a simple right-to-left operation. The borrowing of deficient 10s is performed before the subtraction of the digits, and if there is a series of zeros in the number, the borrowing will have to continue left until a non-zero digit is reached, and all these zeros will have to be changed to nines. Subtraction operations require read and write operations that move in a zigzag fashion.
The 10’s complement addresses this annoying issue of zigzagging areas of attention by introducing a simple subtraction step before performing an addition step.
Illustrating with the following example:
5006002 – 209137
Doing it using the long subtraction way (the normal way):
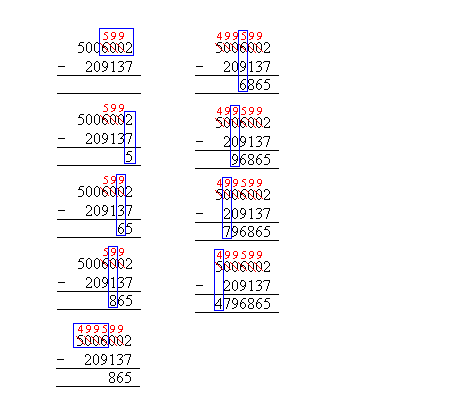
Subtraction of the right-most digits require a borrowed 10 from the digits on the left, thus changing 3 digits on the left. The subtraction process then returns to the first digit and the progressing on to the next.
Of course, the borrowing of 3 digits is consists of 3 distinct steps. If the next number is not capable of providing a 10, in the case of a zero, then the subsequent number will have to be considered until the first non-zero is reached.
The fourth digits also require a borrowed 10, and another 3 digits on the left have to be modified before returning to the actual subtraction.
As one can see, the areas of consideration while going through the subtraction process moves in a saw tooth fashion with intermittent hops left and right.
The 10s complement takes advantage of the fact that 209137 (the subtrahend- the number that is to be removed from 5006002, the minuend) is 999999 – 790862.
209137 = 999999 – 790862
209137 = 999999 – 790862 + 1 – 1
209137 = 1000000 – 790862 – 1
With this in mind, the subtraction can be rewritten as follows:
5006002 – 209137 = 5006002 – (1000000 – 790862 – 1)
5006002 – 209137 = 5006002 + 790862 + 1 – 1000000
The actual calculation procedure is shown below. Doubtless, there are more steps compared to long subtraction, but the business of borrowing is completely eliminated.
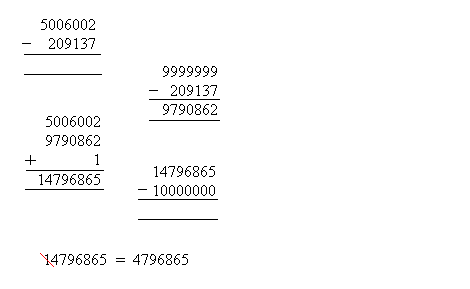
First, the complement of the subtrahend is taken. Sufficiently many digits of 9s must be used as to match the longest string present in the calculation. This is to ensure that the end result can be obtained simply by truncating the most significant digit from the answer.
The minuend is then added to one and the complement of the subtrahend.
Finally, a power of 10 is removed from the sum. If the number of 9’s used in the complementing process is a good choice, this final subtraction is a mere removal of the leading 1, as is the case here.
The explanation and derivation is unwieldy, but when performed with a sheet of paper and a pencil, the 10s complement method is an extremely easy method to reliably calculate subtractions of large numbers.
When working with binary numbers, the complement method is even more effective. This can be justified by the fact that the 2’s complement of binary numbers is trivial to perform.
This is because the complement is done by taking the difference of each digit with the largest number available in the base system, in the case of binary, one.
Due to the fact that 1 – 0 = 1 and 1 – 1 =0, taking the complement of each digit is exactly the same as flipping 1’s to 0’s and vice versa.
Working with binary numbers, here is another example:
110110 – 101
111111 – 000101 = 111010 (bit flipping of the subtrahend, 101)
110110 + 111010 + 1 = 1110001
1110001 – 1000000 = 110001
Therefore, 110110 – 101 = 110001
Mathematics
Labels: applied mathematics, mathematics

<< Home