Option valuation- understanding how price volatility and duration to expiry affects the value of an option
This rather long article is laid out as follows:
Summary:
The price volatility and duration affects options because of the asymmetrical way options payback the holder. High volatility implies a high likelihood for prices to move either up or down. If process move in one direction, the bond holder gains. If prices move in the opposite direction, the option holder does not suffer losses.
Thus, a larger price volatility and longer duration give will almost result in an increase in the value of the option.
Option fundamentals
Options are securities that grant the option holder the right to buy or sell an asset at a predetermined price some time in the future.
An example of an option to buy (a call option) would be an option to buy 100 barrels of crude oil for the price of US$ 7500 in December. The agreed upon price is called the strike price.
If in December, the market price for 100 barrels of crude oil increased to US$8000, the option holder will decide to exercise the option’s right to buy from the option writer at the cheaper price. Thus, the option holder’s profit is US$ 500.
However, if the price instead decreased to US$ 7000, the option holder will be better off buying in the market. So the option will not be exercised, and the option holder does not profit.
Therefore, the call option allows the holder to profit if the asset price increases, but does not result in losses if the asset price decreases. Of course, there is no free lunch; the option has to be purchased at a cost. We will discuss how the price volatility affects the cost of an option.
Valuation approach
The approach taken here is the estimate the expected return from the option position, then discount the value for risk.
Relationship between profit from an option and the asset’s market price
Returning to the above example, we can see that if the asset price is below the strike price, the call option holder does not suffer any losses. But if the asset price is above the strike price, the option holder can buy the asset at the strike price, and then sell the asset in the market at the market price, thus profiting from the difference between market and strike prices.
Figure 1 below shows the relationship between ending price and profit. Notice that if the ending market price is less than the strike price, there are no profit/losses. When ending market price is above the strike price, the profit is the difference between the strike price and the market price.

Figure 1
The probable market price at exercise date of the option
While we may be able to predict certain trends in the market, there will always remain a large element of uncertainty. Likewise, there is an uncertainty regarding the market price of the underlying asset at the expiry of the option. Two factors affect the uncertainty of market price at expiry date: duration to expiry, and volatility of the price.
If the option is to expire next week, and the market price today for 100 barrels of crude oil is US$ 7750, we would expect the price next week to be close to US$ 7750. The probability of a large change is small (but still present: a severe industrial accident in a major refinery could push prices up abruptly).
However, if the option is expiring in 6 months, there is more time for all sorts of market events to cause changes for the price of 100 barrels of oil to move away from the current price of US$ 7750.
In figure 2 below, we illustrate the probability of ending prices. As the graphs show, prices further in the future are more likely to move further from the current price.

Figure 2
The effect of price volatility is similar: assets which are more prone to fluctuation will have a more spread out probability density function than assets which have more stable prices.
How likely is it that I will profit from this option?
Earlier, we have shown that the profit from a call option position is asymmetrical: the holder profits if the asset price is above the strike price, but does not lose if the asset price is below the strike price.
Let’s say the current asset price is 7750, and the strike price is set at 7500. We have two options, one that expires in one week, and one that expires in 6 months. If we were able to exercise NOW, we would definitely gain 250 in profits. But what about 1 week or 6 months later?
Figure 3 below shows that for the one-week option, we will almost certainly be in a profitable position. However, there is a chance of not being profitable if we take the 6-month option. This is because the longer duration increases the likelihood of the asset price moving below the strike price (however, we must not forget that the asset price can also move up higher).
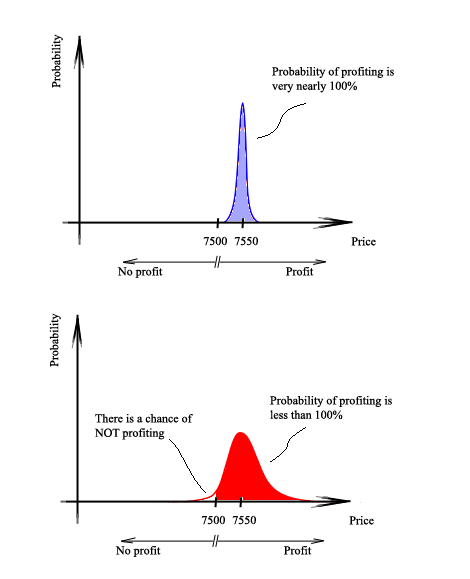
Figure 3
Of course, this is not the end of our analysis. While we can now estimate the likelihood of making a profit, we still need to have a feel of how much we can expect to profit.
How much profit can I expect from this option?
If we are interested in estimating the expected profit from an option position, we need to find the total of the (probability of a particular asset price × the profit at that asset price) for all possible asset prices.
The expected profit from this position is the area below the (probability of a particular asset price × the profit at that asset price) curve. For the position of options expiring in 1 week and 6 months, the calculations are displayed graphically below (these calculations cannot be solved geometrically in a practical manner; a spreadsheet was required to calculate the probability density function, multiply the probability with the profit, and then calculated the area).
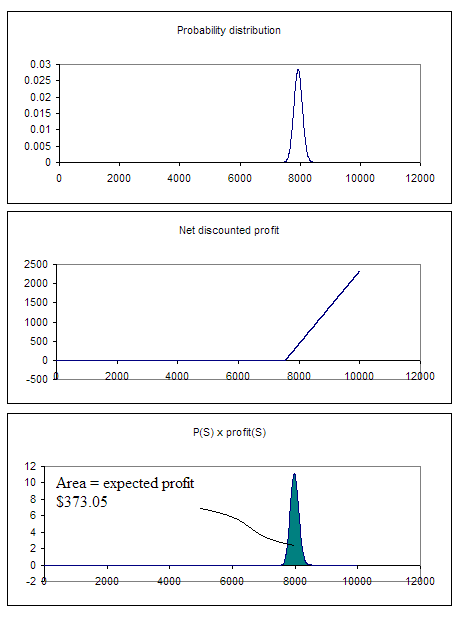
Figure 4

Figure 5
If we compare expected profit and likelihood of profit, we see that the 6 months position has a small likelihood of not profiting (as shown in figure 3) but greater expected profit. This is due to the fact that the 6 month option can earn large profits if the underlying price moves upwards significantly, but make no losses if the price goes below the strike price.
Another example: on the money option
The sensitivity of an option’s value to price volatility and duration is particularly severe for an on the money option. This is an option which has a strike price equal to the current underlying price. We use the same examples as above, but this time the strike price is the same as the current price. If prices move up the slightest bit, the option holder will profit, but if prices move down the slightest bit, option holders will not lose money.
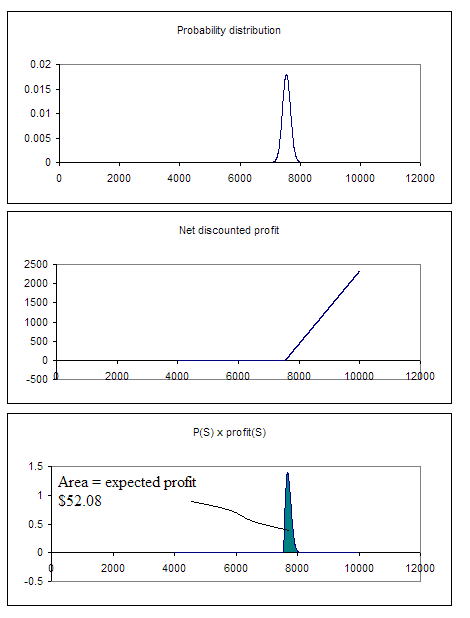
Figure 6
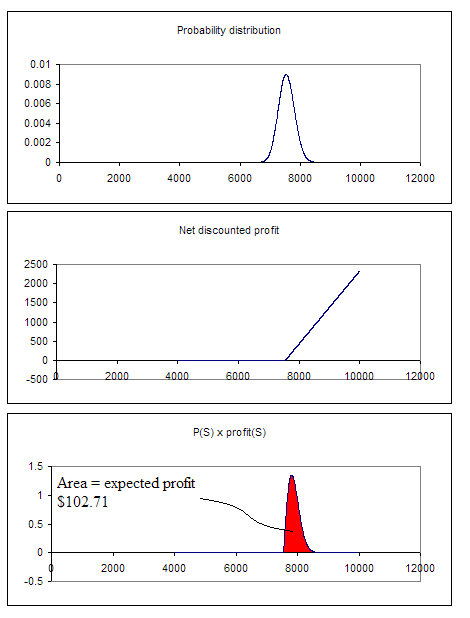
Figure 7
Volotility sensitivity of options
If we were to compare the sensitivity of options, we can see that an on the money option is very sensitive to a change in volatility (in the examples in figures 6 and 7, the expected profit jumps from 52.08 to 102.71, a 97% leap) while an in the money option is less sensitive (in the examples in figures 4 and 5, the expected profit jumps from 373.05 to 381.04, a mere 2% incement).
If an option was deeply out of the money (the strike price is well below the current underlying price), then we expect the option to expire without turning us any profit. Unless we have a massive increase in volatility, the value of this option will be very close to zero regardless of volatility.
Valuing the option
If the option holder is completely indifferent to risk, then the option holder will be willing to pay the expected value of the option in order to own the option.
However, this does not apply in the real world: buyers want to be reimbursed for risk. Thus, buyers will not be willing to pay the full expected value for an option with uncertain returns.
For options that are deeply in or out of the money, the option price will be very close to the expected profit. For in deeply in the money options, the expected profit is equal to the difference between the strike price and current market price (this is also equal to the area under the probability × profit curve). For deeply out of the money options, the expected profit is zero.
For options that have their probability functions straddling the strike price, the option price has to be adjusted for that fact that there could be decent profits or none at all. For volatile or long duration options (figure 7), we will expect the discount to be substantial; for less volatile and shorted duration options (figure 6), the discount will be less.
Summary
Option fundamentals
Valuation approach
Relationship between profit from an option and the asset’s market price
The probable market price at exercise date of the option
How likely is it that I will profit from this option?
How much profit can I expect from this option?
Another example: on the money option
Volatility sensitivity of options
Valuing the option: a hand-waving approach
Summary:
The price volatility and duration affects options because of the asymmetrical way options payback the holder. High volatility implies a high likelihood for prices to move either up or down. If process move in one direction, the bond holder gains. If prices move in the opposite direction, the option holder does not suffer losses.
Thus, a larger price volatility and longer duration give will almost result in an increase in the value of the option.
Option fundamentals
Options are securities that grant the option holder the right to buy or sell an asset at a predetermined price some time in the future.
An example of an option to buy (a call option) would be an option to buy 100 barrels of crude oil for the price of US$ 7500 in December. The agreed upon price is called the strike price.
If in December, the market price for 100 barrels of crude oil increased to US$8000, the option holder will decide to exercise the option’s right to buy from the option writer at the cheaper price. Thus, the option holder’s profit is US$ 500.
However, if the price instead decreased to US$ 7000, the option holder will be better off buying in the market. So the option will not be exercised, and the option holder does not profit.
Therefore, the call option allows the holder to profit if the asset price increases, but does not result in losses if the asset price decreases. Of course, there is no free lunch; the option has to be purchased at a cost. We will discuss how the price volatility affects the cost of an option.
Valuation approach
The approach taken here is the estimate the expected return from the option position, then discount the value for risk.
Relationship between profit from an option and the asset’s market price
Returning to the above example, we can see that if the asset price is below the strike price, the call option holder does not suffer any losses. But if the asset price is above the strike price, the option holder can buy the asset at the strike price, and then sell the asset in the market at the market price, thus profiting from the difference between market and strike prices.
Figure 1 below shows the relationship between ending price and profit. Notice that if the ending market price is less than the strike price, there are no profit/losses. When ending market price is above the strike price, the profit is the difference between the strike price and the market price.

Figure 1
The probable market price at exercise date of the option
While we may be able to predict certain trends in the market, there will always remain a large element of uncertainty. Likewise, there is an uncertainty regarding the market price of the underlying asset at the expiry of the option. Two factors affect the uncertainty of market price at expiry date: duration to expiry, and volatility of the price.
If the option is to expire next week, and the market price today for 100 barrels of crude oil is US$ 7750, we would expect the price next week to be close to US$ 7750. The probability of a large change is small (but still present: a severe industrial accident in a major refinery could push prices up abruptly).
However, if the option is expiring in 6 months, there is more time for all sorts of market events to cause changes for the price of 100 barrels of oil to move away from the current price of US$ 7750.
In figure 2 below, we illustrate the probability of ending prices. As the graphs show, prices further in the future are more likely to move further from the current price.

Figure 2
The effect of price volatility is similar: assets which are more prone to fluctuation will have a more spread out probability density function than assets which have more stable prices.
How likely is it that I will profit from this option?
Earlier, we have shown that the profit from a call option position is asymmetrical: the holder profits if the asset price is above the strike price, but does not lose if the asset price is below the strike price.
Let’s say the current asset price is 7750, and the strike price is set at 7500. We have two options, one that expires in one week, and one that expires in 6 months. If we were able to exercise NOW, we would definitely gain 250 in profits. But what about 1 week or 6 months later?
Figure 3 below shows that for the one-week option, we will almost certainly be in a profitable position. However, there is a chance of not being profitable if we take the 6-month option. This is because the longer duration increases the likelihood of the asset price moving below the strike price (however, we must not forget that the asset price can also move up higher).

Figure 3
Of course, this is not the end of our analysis. While we can now estimate the likelihood of making a profit, we still need to have a feel of how much we can expect to profit.
How much profit can I expect from this option?
If we are interested in estimating the expected profit from an option position, we need to find the total of the (probability of a particular asset price × the profit at that asset price) for all possible asset prices.
The expected profit from this position is the area below the (probability of a particular asset price × the profit at that asset price) curve. For the position of options expiring in 1 week and 6 months, the calculations are displayed graphically below (these calculations cannot be solved geometrically in a practical manner; a spreadsheet was required to calculate the probability density function, multiply the probability with the profit, and then calculated the area).

Figure 4

Figure 5
If we compare expected profit and likelihood of profit, we see that the 6 months position has a small likelihood of not profiting (as shown in figure 3) but greater expected profit. This is due to the fact that the 6 month option can earn large profits if the underlying price moves upwards significantly, but make no losses if the price goes below the strike price.
Another example: on the money option
The sensitivity of an option’s value to price volatility and duration is particularly severe for an on the money option. This is an option which has a strike price equal to the current underlying price. We use the same examples as above, but this time the strike price is the same as the current price. If prices move up the slightest bit, the option holder will profit, but if prices move down the slightest bit, option holders will not lose money.

Figure 6

Figure 7
Volotility sensitivity of options
If we were to compare the sensitivity of options, we can see that an on the money option is very sensitive to a change in volatility (in the examples in figures 6 and 7, the expected profit jumps from 52.08 to 102.71, a 97% leap) while an in the money option is less sensitive (in the examples in figures 4 and 5, the expected profit jumps from 373.05 to 381.04, a mere 2% incement).
If an option was deeply out of the money (the strike price is well below the current underlying price), then we expect the option to expire without turning us any profit. Unless we have a massive increase in volatility, the value of this option will be very close to zero regardless of volatility.
Valuing the option
If the option holder is completely indifferent to risk, then the option holder will be willing to pay the expected value of the option in order to own the option.
However, this does not apply in the real world: buyers want to be reimbursed for risk. Thus, buyers will not be willing to pay the full expected value for an option with uncertain returns.
For options that are deeply in or out of the money, the option price will be very close to the expected profit. For in deeply in the money options, the expected profit is equal to the difference between the strike price and current market price (this is also equal to the area under the probability × profit curve). For deeply out of the money options, the expected profit is zero.
For options that have their probability functions straddling the strike price, the option price has to be adjusted for that fact that there could be decent profits or none at all. For volatile or long duration options (figure 7), we will expect the discount to be substantial; for less volatile and shorted duration options (figure 6), the discount will be less.
Labels: applied mathematics, finance, mathematics

<< Home