Let me show off some mathematical creativity...

Alif suggested I blog this, and I shall humour him.

Yesterday, he presented me with an interesting question:

A car braking from an initial velocity of 60km/h requires 20m to come to a complete stop. What is the braking distance if the initial velocity is increased to 120km/h, assuming the stopping power remains the same?

Here’s the one of the ways one can go about solving the problem:

Initial kinetic energy is half of the product of mass and the square of velocity, 0.5 * m * v^2
Energy dissipated by friction is displacement multiplied by force, s * F.
Since all initial kinetic energy is dissipated, the equations can be combined to form
0.5 * m * v^2 = s * F.
0.5 * m * v ^ 2 / F = s

Since the brake force and mass remain constant, it is clear that braking distance scales with the square of initial velocity. Hence, doubling the initial velocity quadruples the stopping distance.

Here’s the cooler solution (mine, naturally):

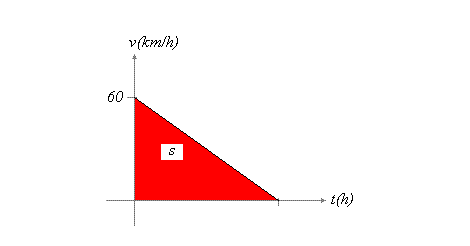
Plot the graph of velocity against time. The area bounded by the curve is the stopping distance. The slope, which is the deceleration, is the same regardless of initial velocity.



Thus the size of the triangular area bounded by the curve can be scaled be adjusting the initial velocity. The area scales with the square of the edge length, so doubling the initial velocity (edge length) quadruples the stopping distance (area).

Look, no equations!

Personal