Marginal production and average production
Note: This post is here because my girlfriend refuses to be impressed by my prowess in calculus.
In economics, the study of costs as a function of production quantity (or vice-versa) is one of the key considerations.
In many cases, it is desirable to know the production quantity that would give the greatest profit margin- this is the condition that gives the highest ratio of production to cost.
The marginal output curve is also of interest, because it will describes the effect of investing additional resources into the venture. Given that we are currently using so much resources to produce so much output, what additional benefit do we get from additional resources spent?
When the marginal output curves and average product (ratio of production to cost) curves are plotted on the same axes, the intersection of these two curves occur at the maximum ratio of production to cost.
This little observation (presented as a statement, without neither explanation or evidence) had disturbed me when I studied macroeconomics in 2002, and also disturbed me when I studied economics yesterday. When I wheeled out the unrivalled fire-power of calculus, all doubts crumbled.
Let x be the resources invested in the venture, and f(x) be the production output resulting from an investment of x.
The marginal production M(x) can be expressed as the first derivative of f(x) with respect to x, the average productions A(x) is the total production over the total cost.
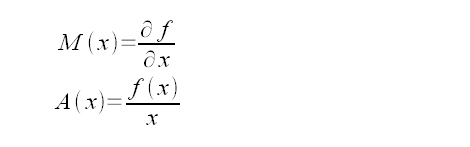
When the average production is maximum, the gradient of A is zero. Therefore, the first derivative of A is equal to zero at the maximum average production.
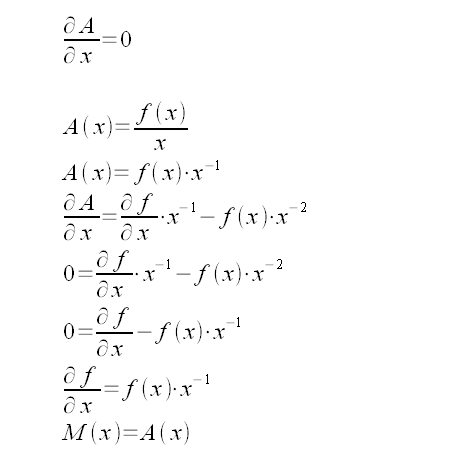
QED.
In economics, the study of costs as a function of production quantity (or vice-versa) is one of the key considerations.
In many cases, it is desirable to know the production quantity that would give the greatest profit margin- this is the condition that gives the highest ratio of production to cost.
The marginal output curve is also of interest, because it will describes the effect of investing additional resources into the venture. Given that we are currently using so much resources to produce so much output, what additional benefit do we get from additional resources spent?
When the marginal output curves and average product (ratio of production to cost) curves are plotted on the same axes, the intersection of these two curves occur at the maximum ratio of production to cost.
This little observation (presented as a statement, without neither explanation or evidence) had disturbed me when I studied macroeconomics in 2002, and also disturbed me when I studied economics yesterday. When I wheeled out the unrivalled fire-power of calculus, all doubts crumbled.
Let x be the resources invested in the venture, and f(x) be the production output resulting from an investment of x.
The marginal production M(x) can be expressed as the first derivative of f(x) with respect to x, the average productions A(x) is the total production over the total cost.
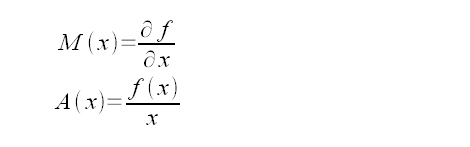
When the average production is maximum, the gradient of A is zero. Therefore, the first derivative of A is equal to zero at the maximum average production.
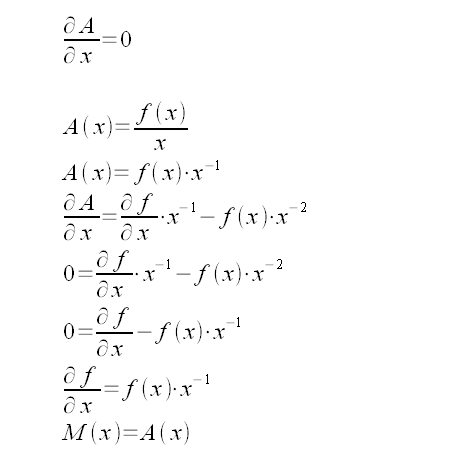
QED.
Labels: applied mathematics, finance

<< Home