The background story on how to imitate the Minolta/Sony Smooth Transition Focus bokeh on regular, large-aperture lenses
This is an investigation of a concept, not the actual building process. This article will involve more mathematics than you’d probably care to read.
Basis of the STF
The STF lens is an innovative lens by Minolta (and now marketed by Sony) that gives exceptionally smooth bokeh by using a piece of grey-coloured glass to regulate light fall-off of the bokeh.
Very simply, this works by making the circle of confusion’s (the bokeh) brightness gradually fade. This is in contrast to normal lenses where the circle of confusion is a very well defined circle (or hexagon/pentagon/octagon, if the aperture blades are slightly closed).
The results are very smeared circles of confusion, as illustrated by the comparison images below.

Photo using a regular, large aperture lens

Photo using an STF lens
The design and ingenuity behind the STF mechanism is described here, with lots of sample photos from the STF lens.
Existing imitation techniques
On Minolta Dynax 7 film cameras, the STF’s smooth bokeh can be mimicked by taking seven exposures on one frame, each exposure with a smaller aperture size. This results in circle of confusions with bright centres and progressively dimmer towards the edge.
Alternatively, a long exposure can be made in dim lighting with the camera mounted on a tripod. The aperture ring can then be manually turned to reduce the aperture over the entire duration of the exposure. For this approach, manual lenses with no aperture clicks are most suitable.
Proposed filter-based mimickery
Here, I propose using a lens filter to reproduce the light falloff that an STF lens’s coloured lens. If a filter can be darkened at the edges to allow a gradual light falloff, then the resulting bokeh will have a similar falloff characteristic. The falloff can be controlled by adjusting the darkness of the glass at different distances from the centre.

Proposed concept: radial gradient neutral density filter
This filter-based approach has been used to shape bokeh, resulting in heart, star, square shaped bokeh:

A heart-shaped bokeh filter

Result from a heart-shaped bokeh filter: circle of confusion (bokeh) partially obscured, resulting in heart shape
Light falloff modelling
Light falloff on the proposed radial ND filter can be done by attempting to mimic the STF lens’s material thickness and how it absorbs light.
The first assumption would be to make an approximation of the filtering element’s lens shape. It is reasonable to assume that the lens is a spherical lens, since spherical lenses are generally much easier to cut than other aspherical shapes.
Based on schematics by Minolta (above), the lens’s geometry can be scaled to a common distance scale based on the lens’s radius:
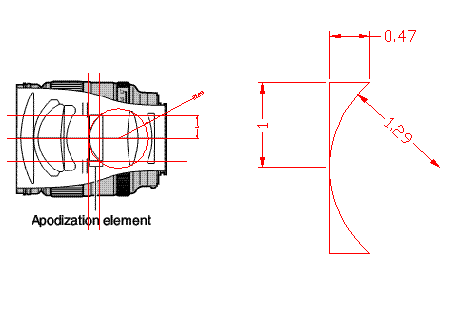
Approximating the coloured glass's dimensions
Lens radius: 1.00r
Lens thickness at centre: ≈ 0
Lens thickness at edge: 0.47r
Sphere radius: 1.29r
After some geometric manipulation, the lens thickness can be expressed by the equation
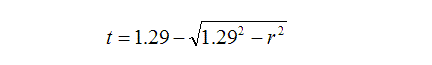
which describes the lens thickness, t, at a particular radius, r.
To calculate the optical density of the glass, it’s useful to note that the aperture number of the Minolta STF lens is f/2.8, but the amount of light let in is equivalent to f/4.5 (the lens’s name is 135mm f2.8 [T4.50] STF). This can tell us that the coloured lens removes approximately 1.4 stops of light, from the following relation:
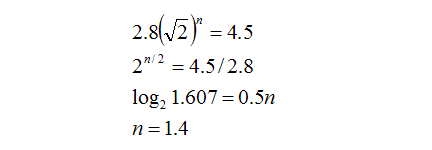
If by removing 1.4 stops of light, this means that only 0.51.4 (39%) of the incoming light passes through; the rest is absorbed by the coloured glass.
In order to select the correct optical density for the filter to match Minolta’s design, we need to match the total light transmitting through the filter to be similar to what Minolta has for the STF lens (39%).
Arbitrarily assuming that the edge of the lens removes p stops of light passing through (similar to the dynamic range of slide film), and using the knowledge that the glass thickness and optical density is proportional, the number of stops removed at a particular radius can be expressed as:
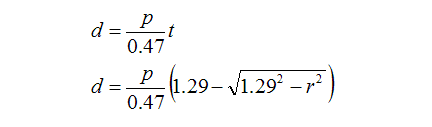
This means that for light passing through any portion of the lens, the quantity that passes through can be expressed as 0.5d. To calculate the total amount of light passing through the entire lens, we need to add intensities of all the different rays of light coming through (some rays weakened due to passing through lots of dark glass, some rays not so weak due to passing through less glass).
The integral below does that:
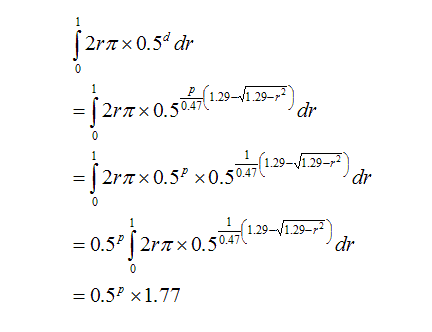
To find the value of p, the above equation needs to match the transmissivity of the Minolta’s coloured lens, which is 39%.
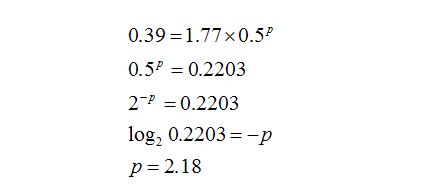
Therefore, the edge of the filter needs to absorb 2.18 stops of light, letting through 22%, while the centre practically lets everything through.
For the proposed filter to match the light falloff of the STF’s bokeh, the filter’s darkness needs to be the same as the STF’s coloured lens. Therefore, the same equation can be used to describe the filter’s darkness at all radiuses:
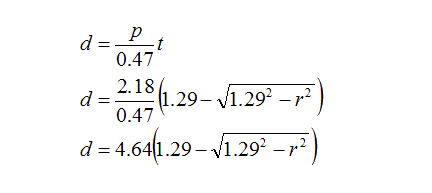
For this equation, the length scale is set such that the filter’s radius is 1.00.
Having obtained the proper light falloff characteristic and the relationship between optical density and radius for the filter, the filter can be constructed. This article will be continued as progress is made during construction.
Basis of the STF
The STF lens is an innovative lens by Minolta (and now marketed by Sony) that gives exceptionally smooth bokeh by using a piece of grey-coloured glass to regulate light fall-off of the bokeh.
Very simply, this works by making the circle of confusion’s (the bokeh) brightness gradually fade. This is in contrast to normal lenses where the circle of confusion is a very well defined circle (or hexagon/pentagon/octagon, if the aperture blades are slightly closed).
The results are very smeared circles of confusion, as illustrated by the comparison images below.

Photo using a regular, large aperture lens

Photo using an STF lens
The design and ingenuity behind the STF mechanism is described here, with lots of sample photos from the STF lens.
Existing imitation techniques
On Minolta Dynax 7 film cameras, the STF’s smooth bokeh can be mimicked by taking seven exposures on one frame, each exposure with a smaller aperture size. This results in circle of confusions with bright centres and progressively dimmer towards the edge.
Alternatively, a long exposure can be made in dim lighting with the camera mounted on a tripod. The aperture ring can then be manually turned to reduce the aperture over the entire duration of the exposure. For this approach, manual lenses with no aperture clicks are most suitable.
Proposed filter-based mimickery
Here, I propose using a lens filter to reproduce the light falloff that an STF lens’s coloured lens. If a filter can be darkened at the edges to allow a gradual light falloff, then the resulting bokeh will have a similar falloff characteristic. The falloff can be controlled by adjusting the darkness of the glass at different distances from the centre.

Proposed concept: radial gradient neutral density filter
This filter-based approach has been used to shape bokeh, resulting in heart, star, square shaped bokeh:

A heart-shaped bokeh filter

Result from a heart-shaped bokeh filter: circle of confusion (bokeh) partially obscured, resulting in heart shape
Light falloff modelling
Light falloff on the proposed radial ND filter can be done by attempting to mimic the STF lens’s material thickness and how it absorbs light.
The first assumption would be to make an approximation of the filtering element’s lens shape. It is reasonable to assume that the lens is a spherical lens, since spherical lenses are generally much easier to cut than other aspherical shapes.
Based on schematics by Minolta (above), the lens’s geometry can be scaled to a common distance scale based on the lens’s radius:

Approximating the coloured glass's dimensions
Lens radius: 1.00r
Lens thickness at centre: ≈ 0
Lens thickness at edge: 0.47r
Sphere radius: 1.29r
After some geometric manipulation, the lens thickness can be expressed by the equation
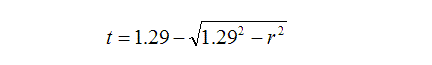
which describes the lens thickness, t, at a particular radius, r.
To calculate the optical density of the glass, it’s useful to note that the aperture number of the Minolta STF lens is f/2.8, but the amount of light let in is equivalent to f/4.5 (the lens’s name is 135mm f2.8 [T4.50] STF). This can tell us that the coloured lens removes approximately 1.4 stops of light, from the following relation:
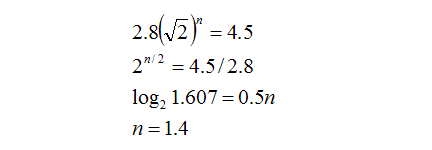
If by removing 1.4 stops of light, this means that only 0.51.4 (39%) of the incoming light passes through; the rest is absorbed by the coloured glass.
In order to select the correct optical density for the filter to match Minolta’s design, we need to match the total light transmitting through the filter to be similar to what Minolta has for the STF lens (39%).
Arbitrarily assuming that the edge of the lens removes p stops of light passing through (similar to the dynamic range of slide film), and using the knowledge that the glass thickness and optical density is proportional, the number of stops removed at a particular radius can be expressed as:
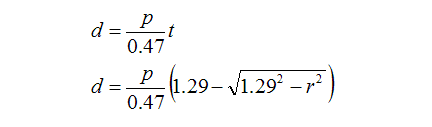
This means that for light passing through any portion of the lens, the quantity that passes through can be expressed as 0.5d. To calculate the total amount of light passing through the entire lens, we need to add intensities of all the different rays of light coming through (some rays weakened due to passing through lots of dark glass, some rays not so weak due to passing through less glass).
The integral below does that:
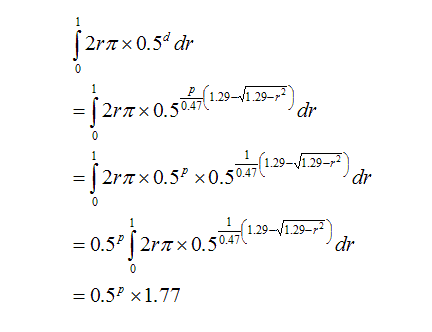
To find the value of p, the above equation needs to match the transmissivity of the Minolta’s coloured lens, which is 39%.
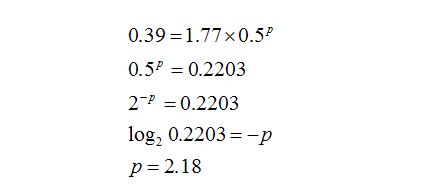
Therefore, the edge of the filter needs to absorb 2.18 stops of light, letting through 22%, while the centre practically lets everything through.
For the proposed filter to match the light falloff of the STF’s bokeh, the filter’s darkness needs to be the same as the STF’s coloured lens. Therefore, the same equation can be used to describe the filter’s darkness at all radiuses:
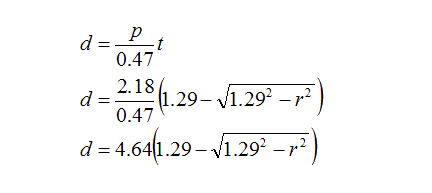
For this equation, the length scale is set such that the filter’s radius is 1.00.
Having obtained the proper light falloff characteristic and the relationship between optical density and radius for the filter, the filter can be constructed. This article will be continued as progress is made during construction.
Labels: applied mathematics, applied science, photographic equipment, photography

<< Home